Le calcul approché d'intégrales ou de limites de sommes avec Python
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Écrire un programme Python permettant de calculer une valeur approchée d’une intégrale.
- Pour déterminer une valeur approchée d’intégrales, on peut utiliser différentes méthodes : la méthode des rectangles, la méthode des milieux, la méthode des trapèzes et la méthode de Monte Carlo.
- Exemple de programme Python traduisant la
méthode des rectangles :
- Exemple de programme Python traduisant la
méthode des milieux :
- Exemple de programme Python traduisant la
méthode des trapèzes :
- Exemple de programme Python traduisant la
méthode de Monte Carlo :
- Utiliser le calcul intégral.
- Calculer des probabilités.
On considère une fonction f définie sur un intervalle [a ; b].
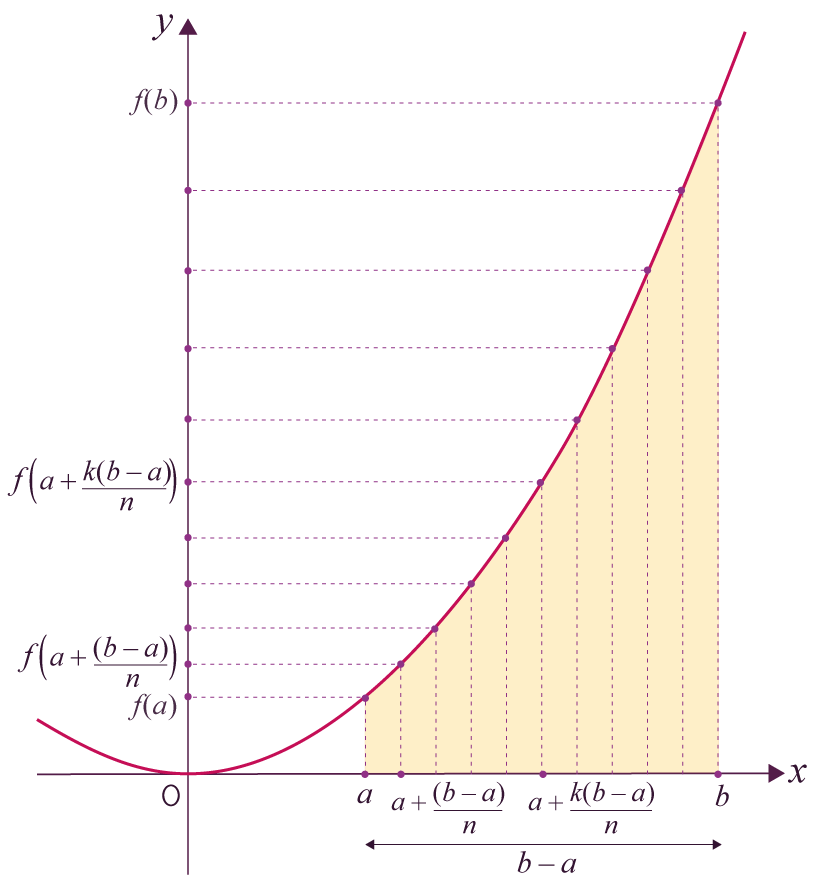
On partage l’intervalle [a ; b] en n intervalles de même amplitude.
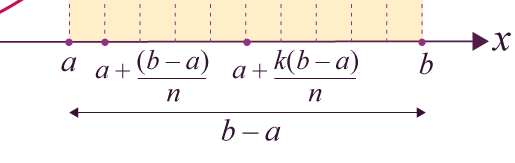
En zoomant sur l’axe des abscisses, on peut remarquer que :
- la longueur de l’intervalle [a ; b] est (b – a) ;
- comme on a découpé l’intervalle
en n parts
égales, on obtient n sous-intervalles de
longueur
;
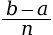- l’intervalle [a ; b]
est alors gradué de la façon
suivante :
a ;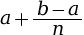
; 
; … ;
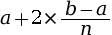b.
La (k + 1)e graduation est donc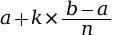
.
Les images de chacune de ces valeurs sont alors
respectivement :
f(a) ;
; … ;
; … ;
f(b).
Soit f une
fonction définie sur un
intervalle I
et a et
b deux
réels de I.
On cherche à déterminer
l’approximation d’une intégrale de
la forme 
, avec a < b,
en estimant l’aire sous la courbe
représentative de la fonction à
l’aide de rectangles situés sous la
courbe.
Pour cela, on se fixe un nombre n de rectangles de
même largeur, tracés de telle façon
que le sommet haut à gauche appartient à
la courbe représentative de f.
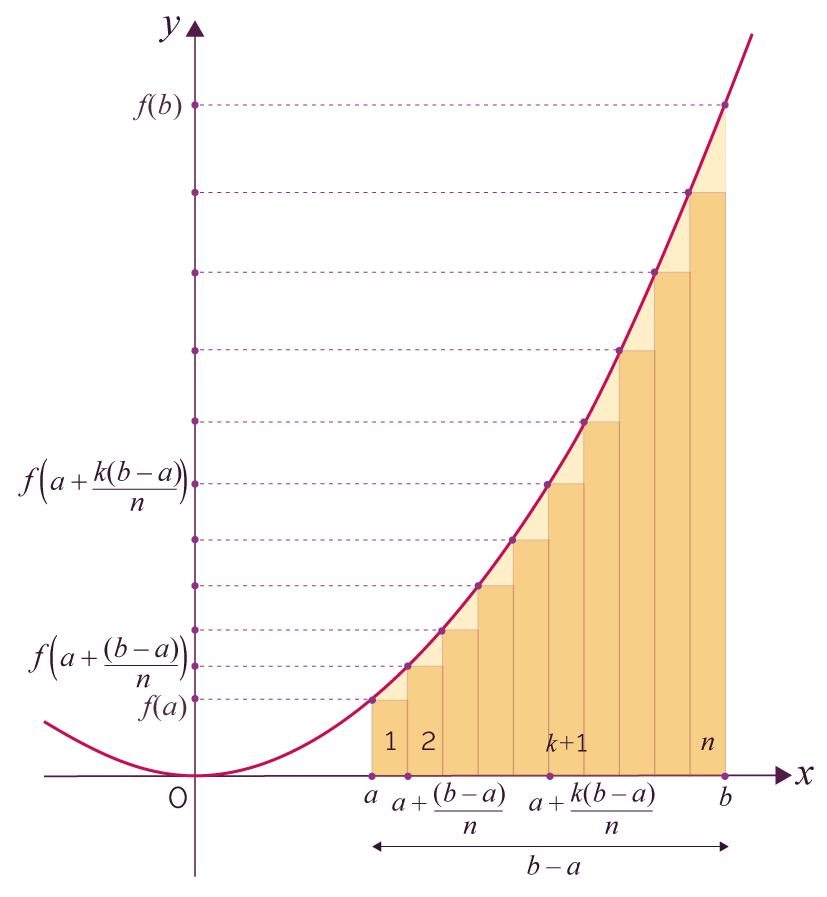
On peut alors calculer l’aire de chacun des
rectangles.
Le premier rectangle a pour longueur f(a) et pour
largeur , donc son aire
est 
.
Le deuxième rectangle a pour
longueur et pour
largeur , donc son aire
est 
.
…
L’aire du (k + 1)e rectangle
est alors 
.
Et l’aire du n-ième rectangle
est égale à 
.
On peut donc écrire que :
On calcule alors cette somme à l’aide de l’algorithme suivant, en langage naturel :
S ← 0
Pour k allant de 0 à (n–1)
S ← S+(b–a)/n×f(a+k×(b–a)/n)
Fin Pour
Retourner S
Fin Fonction
| Programme Python | Commentaires |
|
On déclare la fonction à
intégrer. On traduit en langage Python l’algorithme expliqué dans la partie 2.a. |
Calculons une valeur approchée de l’intégrale
en utilisant le programme
Python décrit précédemment.On peut calculer une première estimation en choisissant de prendre 10 rectangles, puis 1000, puis 10 000 :
- 0,285 arrondie au millième avec 10 rectangles ;
- 0,333 arrondie au millième avec 1000 rectangles ;
- 0,333 arrondie au millième avec 10 000 rectangles.
Plus n est grand, plus l’approximation est précise.
On peut également utiliser la méthode des rectangles à droite. Pour cela, on se fixe un nombre n de rectangles de même largeur tracés tel que le sommet haut à droite appartient à la courbe :
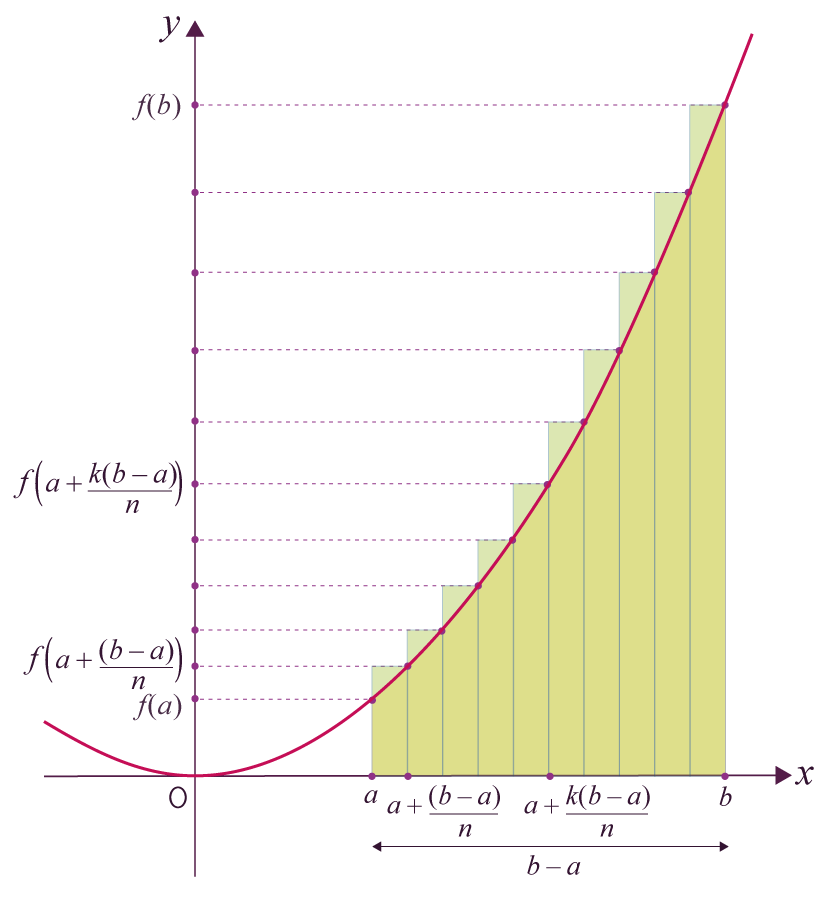
L’aire du (k + 1)e est alors
.Le programme Python devient :
Soit f une
fonction définie sur un
intervalle I
et a et
b deux
réels de I.
On cherche à déterminer
l’approximation d’une intégrale de
la forme 
, avec a < b,
en estimant l’aire sous la courbe
représentative de la fonction à
l’aide de rectangles situés sous la
courbe.
Pour cela, on se fixe un nombre n de rectangles de
même largeur, tracés de telle façon
que le sommet haut à gauche appartient à
la courbe représentative de f.
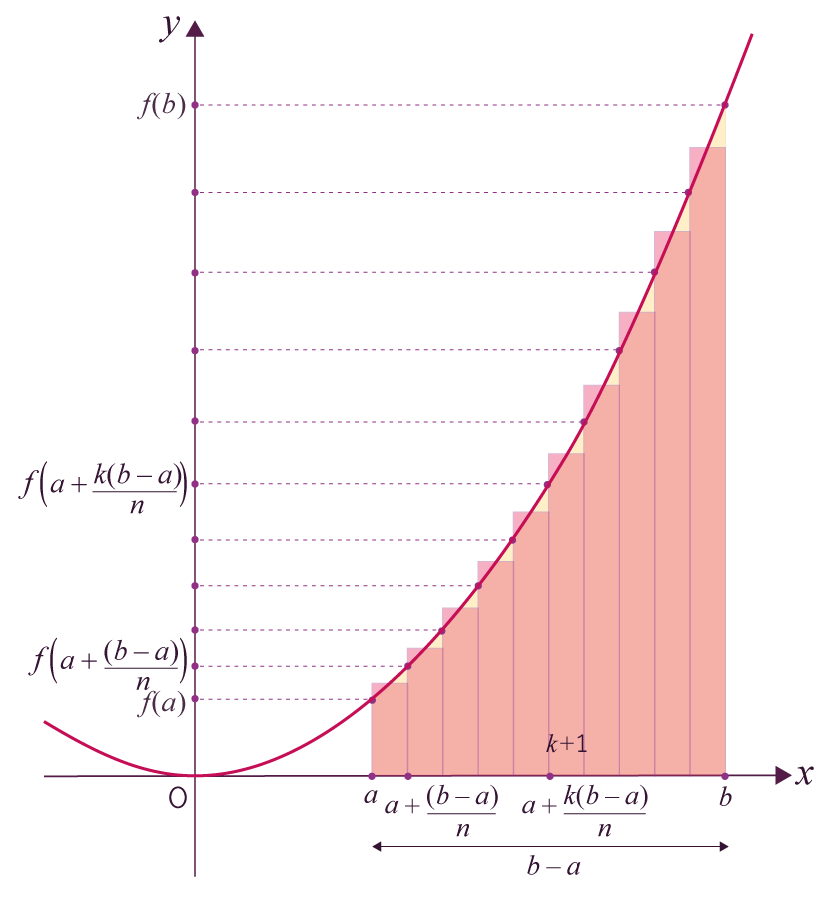
De manière similaire à la méthode
des rectangles, on va calculer l’aire du
(k + 1)e rectangle.
Il a pour largeur et pour longueur
l’image de la moyenne de 
et 
, c’est-à-dire
de 
, soit 
.
Son aire est donc égale
à 
.
On peut donc écrire que :
On calcule alors cette somme à l’aide de l’algorithme suivant, en langage naturel :
S ← 0
Pour k allant de 0 à (n–1)
S ← S+(b–a)/n×f(a+(k+1/2)×(b–a)/n)
Fin Pour
Retourner S
Fin Fonction
| Programme Python | Commentaires |
|
On déclare la fonction à
intégrer. On traduit en langage Python l’algorithme expliqué dans la partie 3.a. |
Calculons une valeur approchée de l’intégrale
en utilisant le programme
Python décrit précédemment.On peut calculer une première estimation en choisissant de prendre 10 rectangles, puis 1000, puis 10 000 :
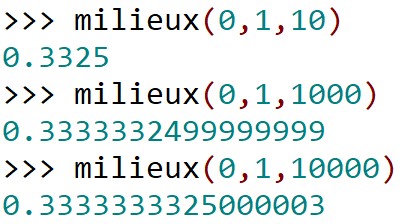
- 0,3325 avec 10 rectangles ;
- 0,333 arrondie au millième avec 1000 rectangles ;
- 0,333 arrondie au millième avec 10 000 rectangles.
Sachant que
,on peut observer
qu’à n égaux les
résultats sont plus précis qu’avec
la méthode des rectangles.
Soit f une
fonction définie sur un
intervalle I
et a et
b deux
réels de I.
On cherche à déterminer
l’approximation d’une intégrale de
la forme 
, avec a < b,
en estimant l’aire sous la courbe
représentative de la fonction f à l’aide
de trapèzes situés sous la courbe.
Pour cela, on se fixe un nombre n de trapèzes de
même hauteur, tracés comme sur la figure
suivante.
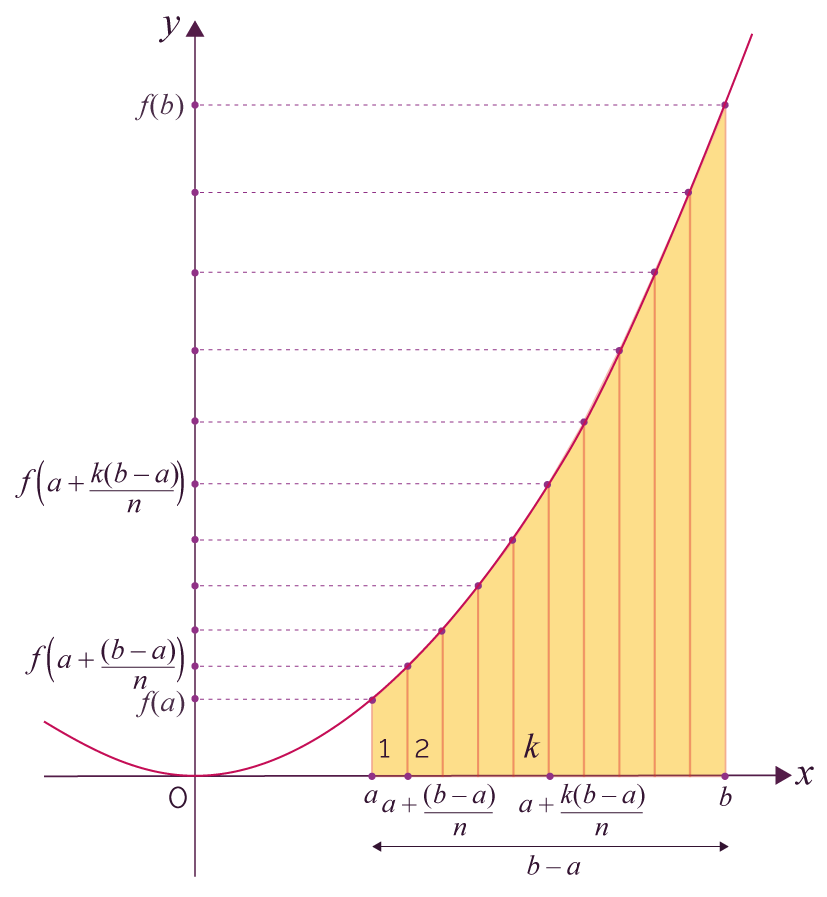
L’aire d’un trapèze est donné
par la relation : 
où h est appelé
hauteur, b petite base et
B grande base.
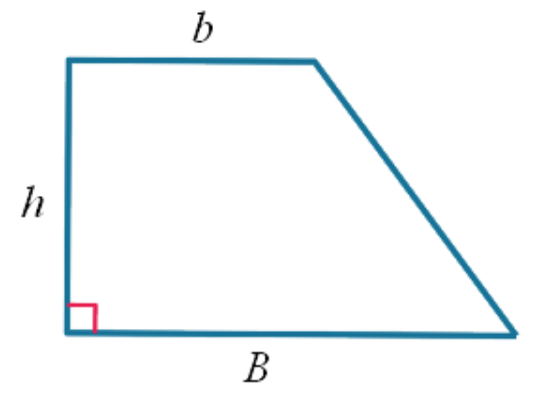
De manière similaire à la méthode
des rectangles, on va calculer l’aire du
k-ième trapèze.
Ses caractéristiques sont les suivantes :
- sa hauteur est égale à
;
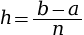- sa grande base est l’image de 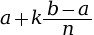, donc
;
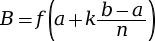- sa petite base est l’image de
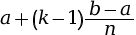, donc 
.
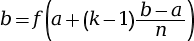Son aire est donc : 
On peut donc écrire que :
On calcule alors cette somme à l’aide de l’algorithme suivant, en langage naturel :
S ← 0
Pour k allant de 1 à n
S ← S+(b–a)/2n×(f(a+(k–1)×(b–a)/n)+f(a+k×(b–a)/n)
Fin Pour
Retourner S
Fin Fonction
| Programme Python | Commentaires |
|
On déclare la fonction à
intégrer. On traduit en langage Python l’algorithme expliqué dans la partie 4.a. |
Calculons une valeur approchée de l’intégrale
en utilisant le programme
Python décrit précédemment.On peut calculer une première estimation en choisissant de prendre 10 rectangles, puis 1000, puis 10 000 :
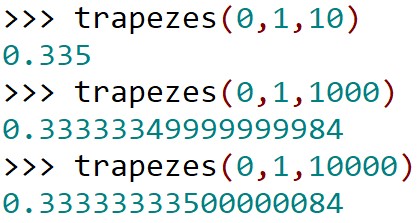
- 0,335 avec 10 rectangles ;
- 0,333 arrondie au millième avec 1000 rectangles ;
- 0,333 arrondie au millième avec 10 000 rectangles.
Soit f une
fonction définie sur un
intervalle I
et a et
b deux
réels de I.
On cherche à déterminer
l’approximation d’une intégrale de
la forme 
, avec a < b,
en estimant l’aire sous la courbe
représentative de la fonction f de manière
statistique.
On commence par déterminer un rectangle de
largeur (b – a)
et de longueur f(m) où
m est
le maximum de la fonction sur
l’intervalle [a ; b].
Comme f
est continue sur [a ; b],
le théorème des valeurs
intermédiaires assure son existence.
En reprenant l’exemple précédent,
on obtient la configuration suivante :
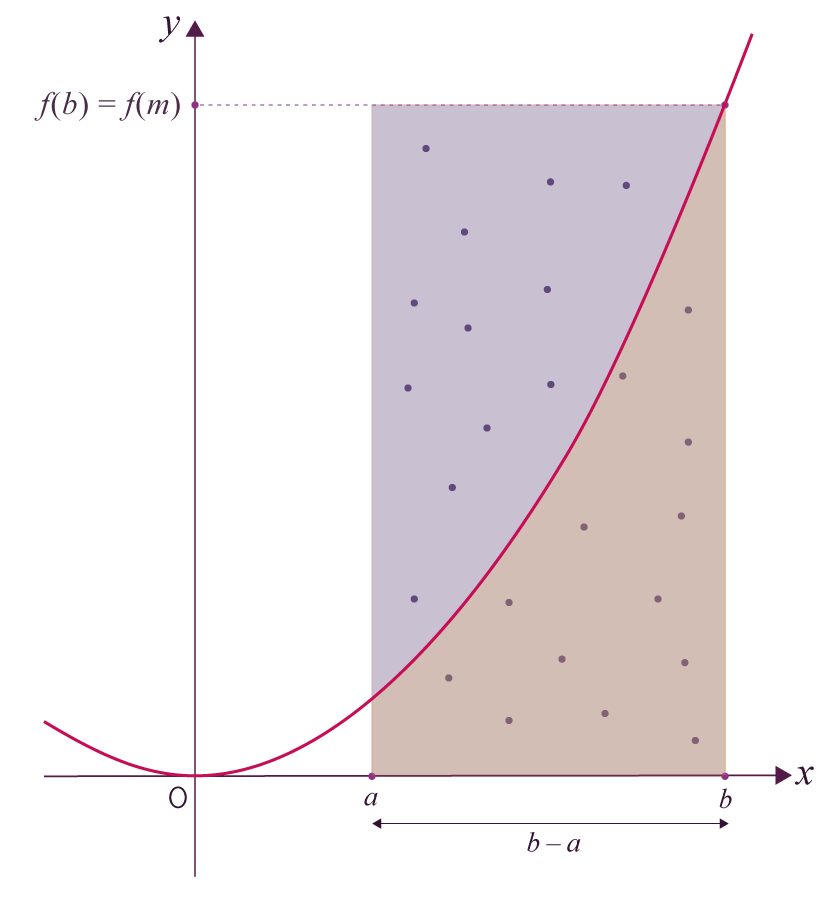
Ici, le maximum est atteint en b.
Si on prend un point au hasard dans ce rectangle, la
probabilité qu’il soit situé sous
la courbe est alors égale à 
où nous avons :
-
As est
l’aire située sous la courbe, donc
;
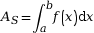- AR est l’aire du rectangle, donc AR = (b – a)f(m).
On en déduit donc que : 
Comme on ne connait pas la
probabilité p, on peut l'estimer en
prenant un nombre N de points au hasard
dans le rectangle et en comptant le
nombre n d’entre eux
situés sous la courbe.
La fréquence définie par 
est alors une approximation
de p.
Plus N
est grand, plus f est proche
de p.
On a donc 
avec f la fréquence
des points obtenus sous la courbe.
Pour générer des points au hasard dans le rectangle, il suffit de générer :
- une abscisse x comprise entre a et b avec la commande random ;
- une ordonnée y comprise entre 0 et f(m) avec la commande random.
Si y ≤ f(x), alors le point est sous la courbe, sinon il est au-dessus. Pour N points obtenus de manière aléatoire, on a donc l’algorithme suivant, en langage naturel :
n ← 0
Pour k allant de 1 à N
x ← random(a,b)
y ← random(0,f(m))
Si yf(x) alors
n ← n+1
Fin Si
Fin Pour
I ← (n/N)×(b–a)×f(m)
Retourner I
Fin Fonction
I est l’approximation de l’intégrale.
| Programme Python | Commentaires |
|
On importe la bibliothèque random. On déclare la fonction. On écrit avec la commande return l’expression de la fonction, ici la fonction carré. On traduit en langage Python l’algorithme expliqué dans la partie 5.a. La fonction uniform(a,b) génère aléatoirement un nombre réel compris entre a et b. |
Calculons une valeur approchée de l’intégrale
en utilisant le programme
Python décrit précédemment.On sait que la fonction carré admet un maximum en 1 sur l’intervalle [0 ; 1]. On peut calculer une première estimation en choisissant de prendre 10 points, puis 1000, puis 10 000 :
- 0,1 avec 10 points ;
- 0,333 arrondie au millième avec 1000 points ;
- 0,333 arrondie au millième avec 10 000 points.
La génération des points étant aléatoire, chaque usage de la fonction renverra un résultat légèrement différent. Voici un échantillon de trois approximations à l’aide de 10 000 points.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Mathématiques
Listes en Python : application aux statistiques et probabilités- Terminale- Mathématiques
Mathématiques
Listes en Python : application aux suites et aux fonctions- Terminale- Mathématiques
Mathématiques
Listes en Python : application à la géométrie plane- Terminale- Mathématiques
Mathématiques
Listes en Python : application aux ensembles
Mathématiques
Listes en Python : création et manipulation- Terminale- Mathématiques
Mathématiques
Le calcul approché de nombres remarquables avec Python
Mathématiques
L'inégalité de Bienaymé-Tchebychev
Mathématiques
Des applications de l'inégalité de Bienaymé-Tchebychev
Mathématiques
Asymptote parallèle à l'un des axes de coordonnées
Mathématiques
Fonctions dérivables
Mathématiques
Règles de dérivation
Mathématiques
Dérivée et étude d'une fonction
Mathématiques
Dérivation d'une fonction composée
Mathématiques
Les fonctions du type exp(u) et ln(u)
Mathématiques
Le raisonnement par récurrence
Mathématiques
Primitives d'une fonction
Mathématiques
Primitives et fonctions composées
Mathématiques
Intégration par parties
Fermer
Accédez gratuitement à
