Le calcul approché de nombres remarquables avec Python
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Écrire un programme Python permettant de calculer une valeur approchée de nombres remarquables.
- Les programmes Python suivants permettent de déterminer les valeurs approchées des nombres remarquables π, e, ln(2), ainsi que du nombre d’or, noté φ.
- Approximation du nombre π

- Approximation du nombre e

- Approximation du nombre ln(2)

- Approximation du nombre d’or

- Étudier des suites numériques.
- Utiliser le calcul intégral.
Le principe d’Archimède consiste à trouver géométriquement l'encadrement du nombre en considérant deux polygones réguliers : l’un inscrit (rose) et l’autre circonscrit (bleu) à un cercle de rayon 1.
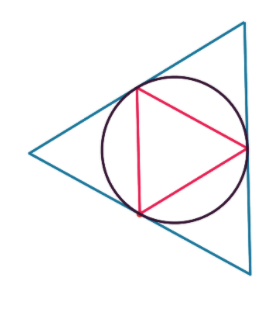 Triangle équilatéral |
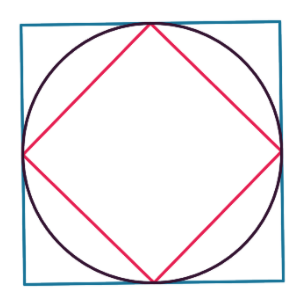 Carré |
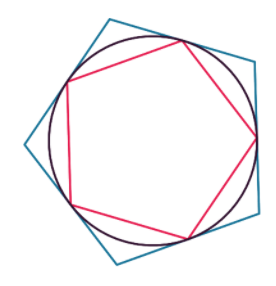 Pentagone régulier |
... |
 Dodécagone |
On remarque que les périmètres des deux
polygones convergent vers celui du cercle lorsque
n devient
grand.
On peut démontrer que, pour
tout n
entier supérieur ou égal
à 3 :
- le périmètre du polygone circonscrit
est donné par :

- le périmètre du cercle de rayon 1 est donné par : P = 2π
- le périmètre du polygone inscrit est
donné par :

On a donc l’inégalité
suivante : ![]() .
.
D’où : ![]() .
.
Soit, en posant ![]() et
et ![]() : In ≤ π ≤ Cn.
: In ≤ π ≤ Cn.
En particulier, on a pour n = 3 :
![]() et
et ![]() .
.
Pour obtenir une approximation de π avec une
erreur e, il suffit de calculer
les termes des deux suites jusqu'à ce que :
Cn – In ≤ e.
Pour résumer, cet algorithme s’écrit en langage naturel de la façon suivante :
n ← 3
C ← 3racine(3)
I ← 3racine(3)/2
Tant que C–I > e
n ← n+1
C ← n×tan(pi/n)
I ← n×sin(pi/n)
Fin Tant que
Retourner (I+C)/2
Fin Fonction
| Programme Python | Commentaires |

|
On importe la bibliothèque math. On traduit en langage Python l’algorithme expliqué dans la partie 1.a. On retourne la moyenne de C et I pour une meilleure approximation. |
En langage Python, la racine carrée se note sqrt().
On peut utiliser le programme Python décrit précédemment pour trouver la valeur approchée de π à 0,1, puis à 0,01, et enfin à 0,0001 près de π :
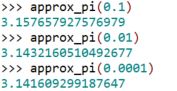
L’approximation à 0,01 près est donc 3,14.
L’approximation à 0,0001 près est donc 3,1416.
En langage Python, les nombres décimaux s’écrivent avec un point et non avec une virgule.
Une façon de trouver une approximation
de e est de
calculer la somme suivante : ![]()
avec n! = 1 × 2 × 3 × … × n,
appelé factorielle de n.
Pour trouver une approximation de e, on va écrire deux fonctions : une première qui détermine la factorielle d’un nombre, puis une seconde qui donne l’approximation de e.
En langage naturel, les deux fonctions s'écrivent de la façon suivante :
f ← 1
Pour i allant de 1 à n
f ← f×i
Fin Pour
Retourner f
Fin Fonction
e ← 0
Pour i allant de 1 à n
e ← e+1/(factorielle(i))
Fin Pour
Retourner e
Fin Fonction
| Programme Python | Commentaires |

|
On importe la bibliothèque math. On traduit en langage Python la fonction factorielle. Puis on traduit en langage Python la fonction qui donne l’approximation de e. |
On utilise le programme Python décrit précédemment pour trouver la valeur approchée de e pour n valant 10, puis 100, puis 1000 :
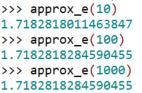
La suite converge rapidement. On voit que, pour n = 100, on a la même approximation que pour n = 1000. Il suffit de prendre n = 18 pour obtenir l’approximation.
L’algorithme de Brouncker sert à donner
une approximation de ln 2. On commence par
remarquer que : ![]() .
.
On cherche donc à déterminer l’aire
sous la courbe de la fonction inverse sur
l’intervalle [1 ; 2].
Pour déterminer cette aire, on pave
successivement l’aire sous la courbe en
plaçant des rectangles les plus grands
possibles.
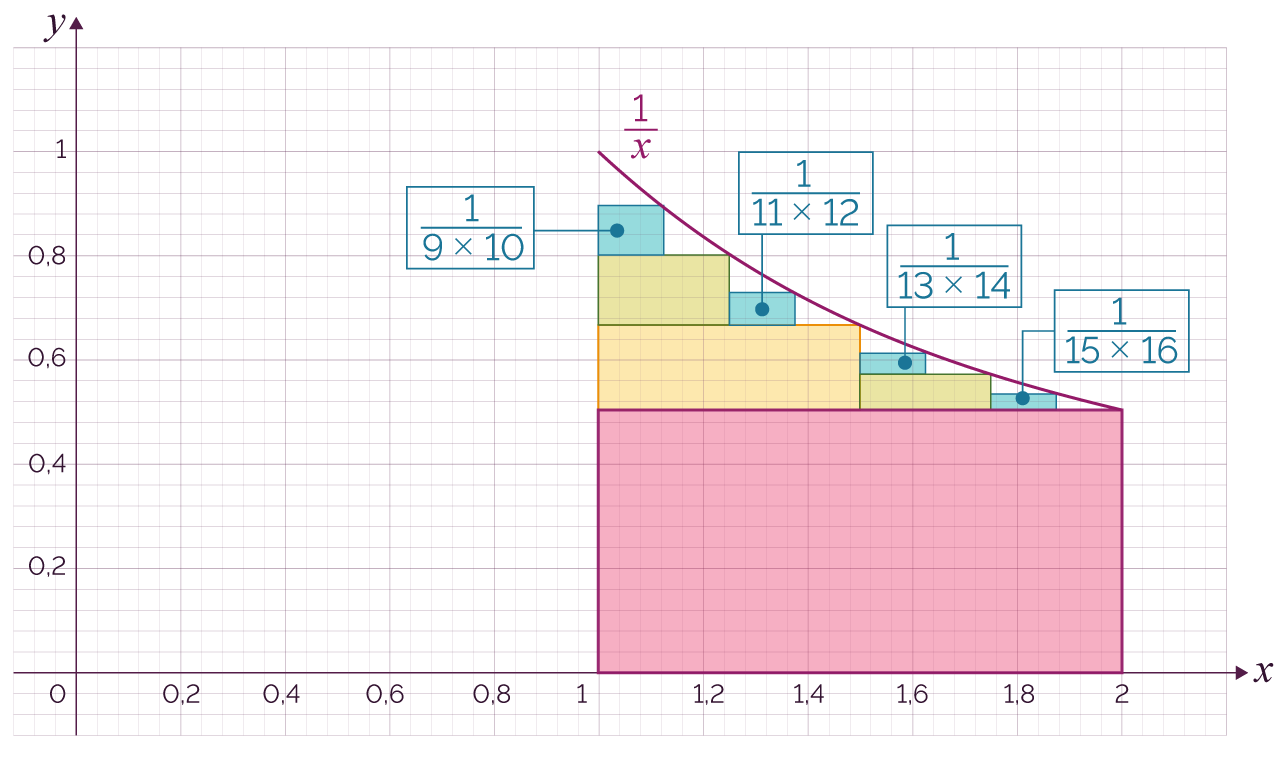
Voici les 4 premières étapes :
| Étape | Graphique | Commentaire |
| 1 |
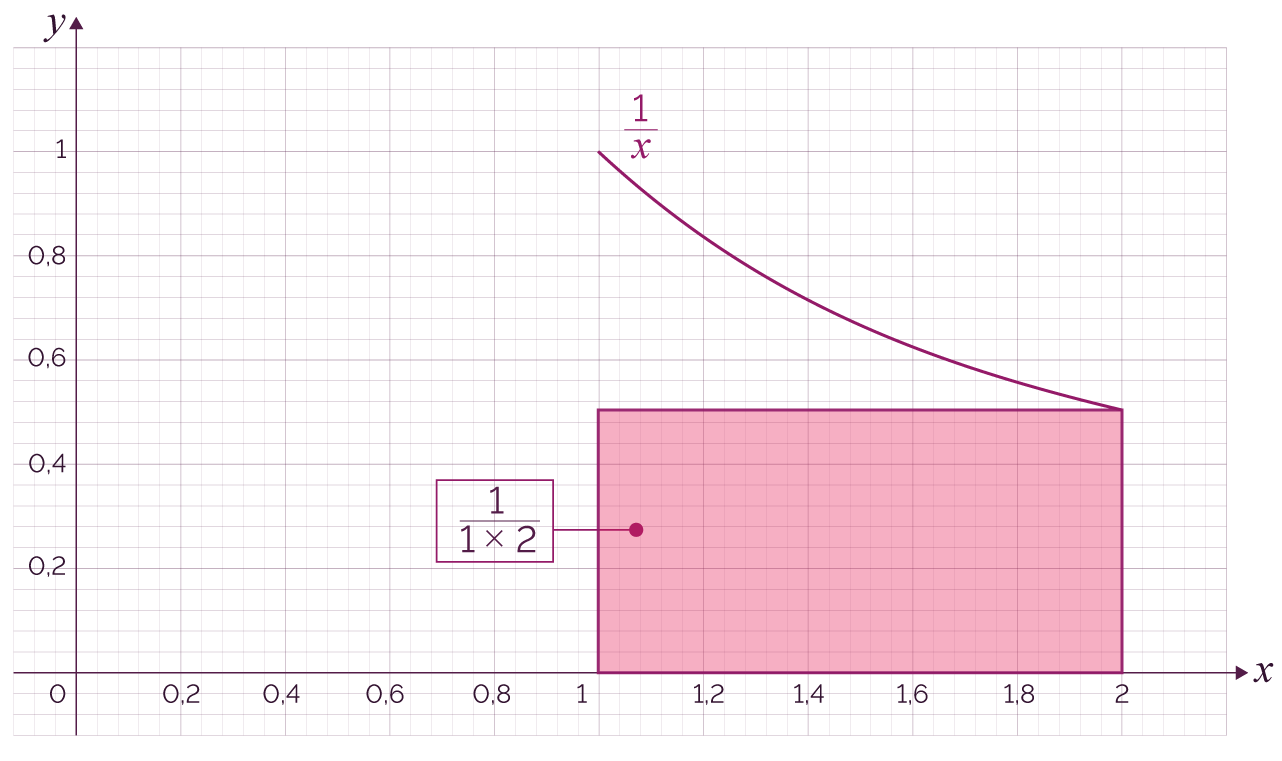
|
On construit un premier rectangle et on peut
alors estimer que ln 2 est environ
égal à |
| 2 |
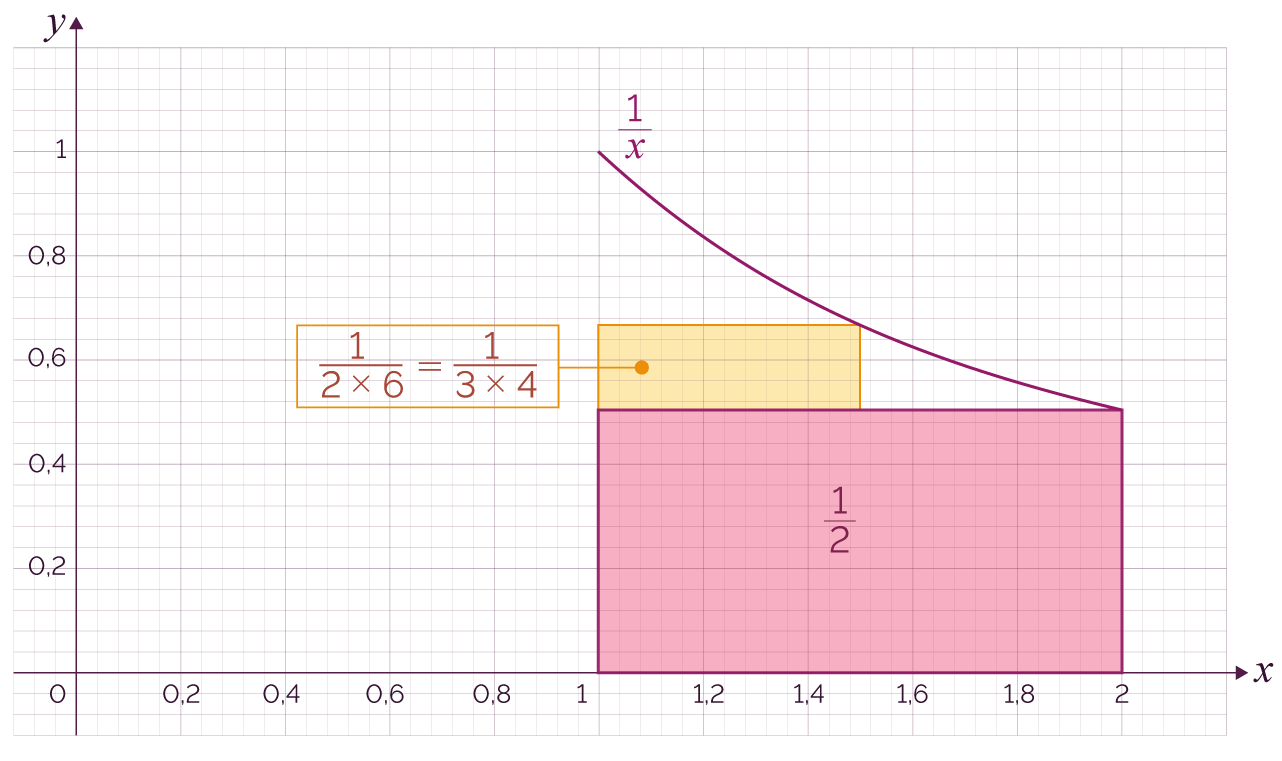
|
On complète la partie restante d’un
autre rectangle et on peut alors estimer que
ln 2 est
environ égal à |
| 3 |
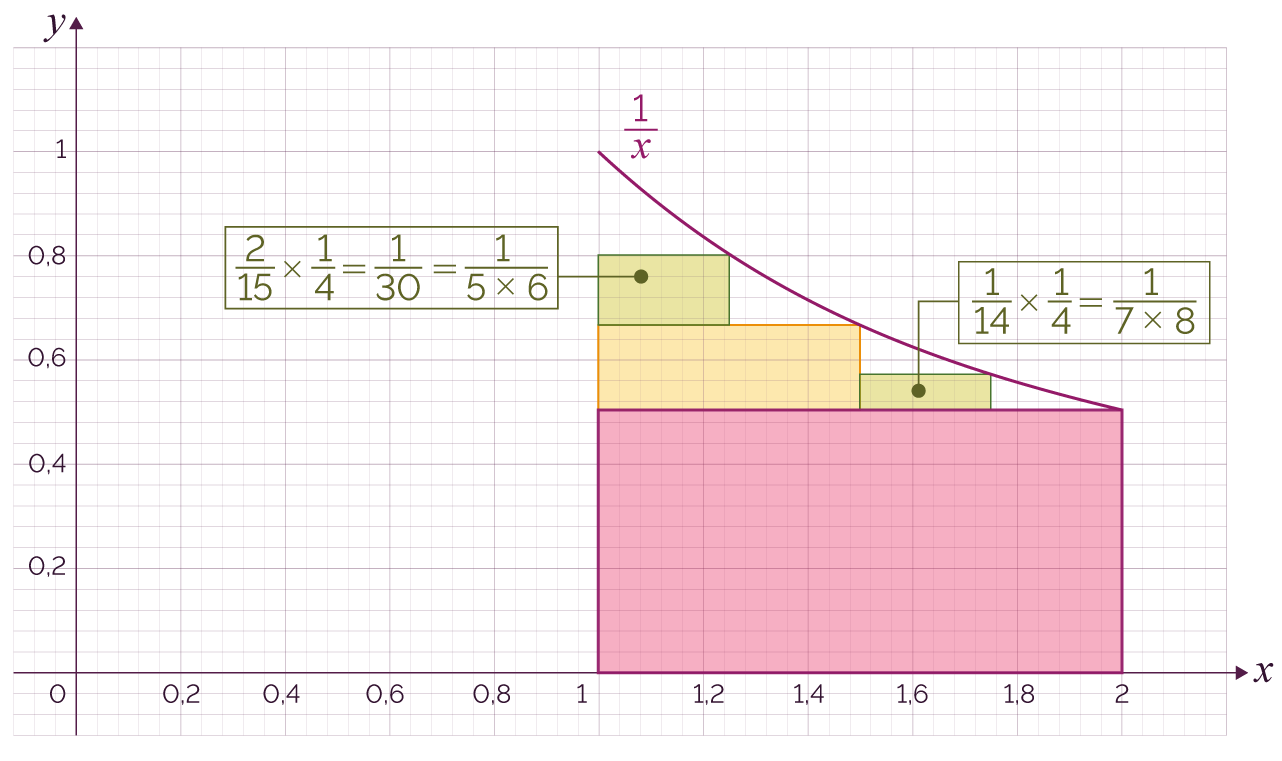
|
On complète encore chacune des deux zones
restantes par des rectangles et on peut alors
estimer que ln 2 est environ
égal à |
| 4 |
|
On complète chacune des quatre zones
restantes par des rectangles et on peut alors
estimer que ln 2 est environ
égal à |
On continue de la même manière
jusqu’à la n-ième étape.
Pour tout n entier naturel, on a
donc : ![]() .
.
On obtient donc l’algorithme suivant, en langage naturel :
S ← 0
Pour i allant de 1 à n avec un pas de 2
S ← S+1/(i×(i+1))
Fin Pour
Retourner S
Fin Fonction
| Programme Python | Commentaires |

|
On traduit en langage Python la fonction qui donne l’approximation de ln 2. |
On utilise le programme Python décrit précédemment pour trouver la valeur approchée de ln 2 pour n valant 10, puis 100, puis 1000 :
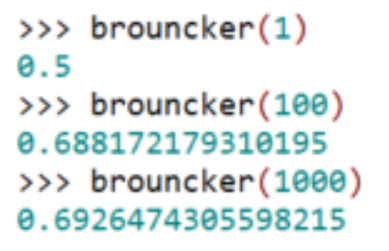
La suite converge lentement, on voit que, pour n = 1000, l’approximation fournie ne l’est qu'avec une précision de 10–2.
Deux longueurs strictement positives a et b respectent la
proportion du nombre d’or si et seulement
si : ![]() .
.
En remarquant que ![]() , et en notant
, et en notant
![]() , on obtient alors :
, on obtient alors :
![]() .
.
On appelle φ le
nombre d’or.
On pose alors la suite (φn)
définie par : φ0 = 1 et, pour tout
entier naturel n, ![]() .
.
On peut alors démontrer que (φn)
converge vers φ.
On obtient donc l’algorithme suivant, en langage naturel :
Phi ← 0
Pour i allant de 1 à n
Phi ← 1+1/Phi
Fin Pour
Retourner Phi
Fin Fonction
| Programme Python | Commentaires |

|
On traduit en langage Python la fonction qui donne l’approximation du nombre d’or. |
On utilise le programme Python décrit précédemment pour trouver la valeur approchée du nombre d’or pour n valant 10, puis 100, puis 1000 :
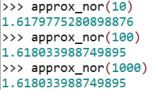

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









