Mesurer les inégalités- Première- SES
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Connaitre les différents calculs pour mesurer les inégalités.
- Il est possible de mesurer la disparité, la dispersion et la concentration des variables afin de faire ressortir la mesure des inégalités.
L'un des savoir-faire basiques consiste à calculer la disparité, la dispersion ou la concentration des variables. Plus généralement, ce qui est abordé ici est la mesure des inégalités.
La disparité mesure les écarts
entre les valeurs d'une variable. Ces
écarts peuvent être exprimés
en unités quelconques,
c'est-à-dire en euros, en kilos, en
mètres... On parle alors de
disparité absolue.
Mais la disparité peut aussi être
exprimée en valeur relative,
on parle alors de disparité
relative. Celle-ci est
généralement exprimée sous la forme
d'un coefficient multiplicateur mais
elle peut aussi être sous forme
d'indice ou de
pourcentage.
Soient les données suivantes relatives aux salaires annuels moyens en France en 2005, selon les catégories socioprofessionnelles (CSP), en euros :
| CSP | Salaires annuels moyens |
|
Cadres Professions intermédiaires Employés Ouvriers Ensemble |
45 330 23 140 16 080 16 900 22 850 |
- disparité absolue : en 2005, la disparité absolue de salaires entre les cadres et l'ensemble des salariés est de 45 330 - 22 850 = 22 480 €
- disparité relative : celle-ci est de 45 330 / 22 850 = 1,98, ce qui signifie que le salaire des cadres est 1,98 fois plus élevé que celui de l'ensemble des salariés. De la même manière, on peut montrer qu'entre les ouvriers et l'ensemble de la population concernée la disparité relative est de 16 900 / 22 850 = 0,74 (le salaire des ouvriers s'élève donc à 74 % du salaire moyen de la population).
La dispersion d'une série statistique
s'intéresse à l'étendue des
écarts entre les valeurs extrêmes d'une
série. Cependant, les valeurs maximales
et minimales sont souvent exceptionnelles et donc peu
représentatives.
Pour contourner cette difficulté, la population
est alors divisée en un nombre défini de
groupes de tailles égales délimitées
par certaines valeurs de la variable
étudiée : les
quantiles. Il s'agit de :
- quartiles si la population est répartie en quatre groupes,
- de quintiles si la population est divisée en cinq groupes,
- de déciles en dix groupes,
- et de centiles en cent groupes.
Chaque quantile est donc de taille égale. Ainsi,
par exemple, on appelle décile les seuils de la
variable entre lesquelles se situe un dixième de
la population.
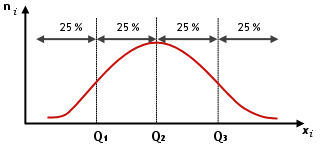
La dispersion interquartile peut
être représentée de la manière
suivante :
Soient les données relatives à la distribution des salaires annuels nets, en 2005, en euros courants :
| Déciles | Salaires annuels nets |
|
D1 D2 D3 D4 D5 ( médiane) D6 D7 D8 D9 |
12 506 13 955 15 278 16 695 18 336 20 373 23 086 27 399 36 349 |
Le tableau indique, dans le cas du premier décile (D1), que 10 % des salariés ont, en 2005, un salaire inférieur à 12 506 €. Le cinquième décile correspond à la médiane, c'est-à-dire à la valeur de la variable qui partage la population en deux groupes de tailles équivalentes. Comme vous le voyez, il y a neuf groupes ici (D1 à D9) ; le décile D9 signifie que 10 % de la population se situe à un niveau de la variable supérieure à 36 349 € (ce sont les salariés les mieux payés).
Pour mesurer le degré de dispersion, il devient
possible de mesurer l'écart entre les deux groupes
extrêmes et non entre les valeurs
extrêmes ; on utilise pour cela deux
outils :
- l'intervalle interquantile : celui-ci s'obtient en mesurant la différence entre les quantiles extrêmes. La population comprise dans l'intervalle interdécile par exemple (cas de l'exemple) est 80 % de l'ensemble, car les deux déciles extrêmes sont exclus.
Dans la distribution des salaires, on a alors :
D9 – D1 = 36 349 – 12 506 = 23 843 €.
- le rapport interquantile : celui-ci s'obtient en faisant le rapport entre les quantiles extrêmes.
Le rapport interdécile est D9 / D1, soit 36 349 / 12 506 = 2,91, ce qui signifie que les 10 % des salariés les mieux payés bénéficient au minimum d'un salaire 2,91 fois plus élevé que celui des 10 % les moins bien payés. Le calcul interdécile est très révélateur des inégalités au sein d'une population.
Contrairement aux calculs de disparités et de dispersion, les mesures de concentration cherchent à évaluer les inégalités en prenant en compte l'ensemble des valeurs que prend la variable dans la population étudiée en combinant une représentation graphique, la courbe de Lorenz, et un indicateur statistique, le coefficient de Gini :
- la représentation graphique de la dispersion et de la concentration ou la courbe de Lorenz : si l'on représente par un graphique (sur lequel l'axe des abscisses figure les pourcentages cumulés de la population et l'axe des ordonnées les pourcentages cumulés de la variable concernée) cette situation théorique où la variable est répartie de façon strictement égalitaire, on obtient une droite à 45°, dite droite d'équirépartition, bissectrice de l'angle formé par l'axe représentant les pourcentages cumulés de la population (x) et celui représentant les pourcentages cumulés de la variable (y).
La courbe, également appelée courbe de Lorenz, représente la situation la plus souvent réellement observée. Elle se situe donc en dessous, et à droite, de la droite d'équirépartition.
On dispose de données suivantes relatives à la concentration du revenu en France en 2004 :
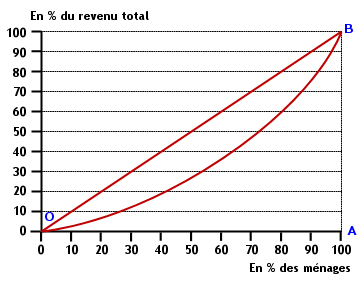
Ainsi, dans cet exemple, on peut montrer que :
- les 10 % des ménages dont les revenus sont les plus faibles se partagent 3,1 % des revenus,
- les 20 % des ménages dont les revenus sont les plus faibles se partagent 7,6 % des revenus,
- les 10 % des ménages dont les revenus sont les plus élevés se partagent 24,8 % des revenus
- et que les 90 % des ménages dont les revenus sont les plus faibles se partagent 75,2 % des revenus.
La répartition aurait été parfaitement égalitaire si la courbe de Lorenz avait été confondue avec la première bissectrice : les 10 % des ménages dont les revenus sont les plus faibles et les 10 % dont les revenus sont les plus élevés auraient alors la même part du revenu total, c'est-à-dire 10 %. Autrement dit, plus la courbe de Lorenz est éloignée de la première bissectrice, plus les inégalités sont fortes ; plus elle s'aplatit en se rapprochant de la diagonale, et plus les inégalités sont faibles.
- un indicateur statistique de la concentration ou l'indice de Gini : également appelé coefficient de Gini, l'indice de Gini mesure la concentration d'une variable au sein d'une population. Il se calcule à partir de la courbe de Lorenz et il est compris entre 0 (absence de concentration car la répartition est parfaitement égalitaire) et 1 (concentration totale car la répartition est parfaitement inégalitaire). C'est le rapport entre la surface comprise entre la courbe de Lorenz et la diagonale OB d'une part, et la surface du triangle OAB d'autre part. Plus le coefficient de Gini est proche de 1, plus la concentration de la grandeur étudiée est forte.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









