Caractériser des signaux
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Comprendre que les signaux sont porteurs d’informations.
- Caractériser un signal en fonction de son type.
- Savoir reconnaitre les caractéristiques des signaux de types logiques, analogiques et numériques.
- Un signal électrique est soit analogique soit numérique. Un signal analogique évolue de façon continue en fonction du temps, tandis qu’un signal numérique évolue de manière discontinue, en ne prenant que deux valeurs possibles.
- Lorsque le signal analogique est périodique (présence d’un motif élémentaire qui se répète), il est caractérisé par sa période, sa fréquence, sa valeur moyenne et sa valeur efficace.
- Lorsque le signal numérique est périodique, il est caractérisé par son rapport cyclique.
- L’acquisition de l’information
- Les différents capteurs
Un signal transmet une information qui peut être un son, une image, une vidéo, un texte, etc.
Un signal est porteur d’une grandeur physique variable qui contient l’information à transmettre entre un émetteur et son récepteur.
Il existe une multitude de signaux qui permettent de caractériser des informations de nature différente. On se limite ici aux signaux électriques qui peuvent être analogiques ou numériques.
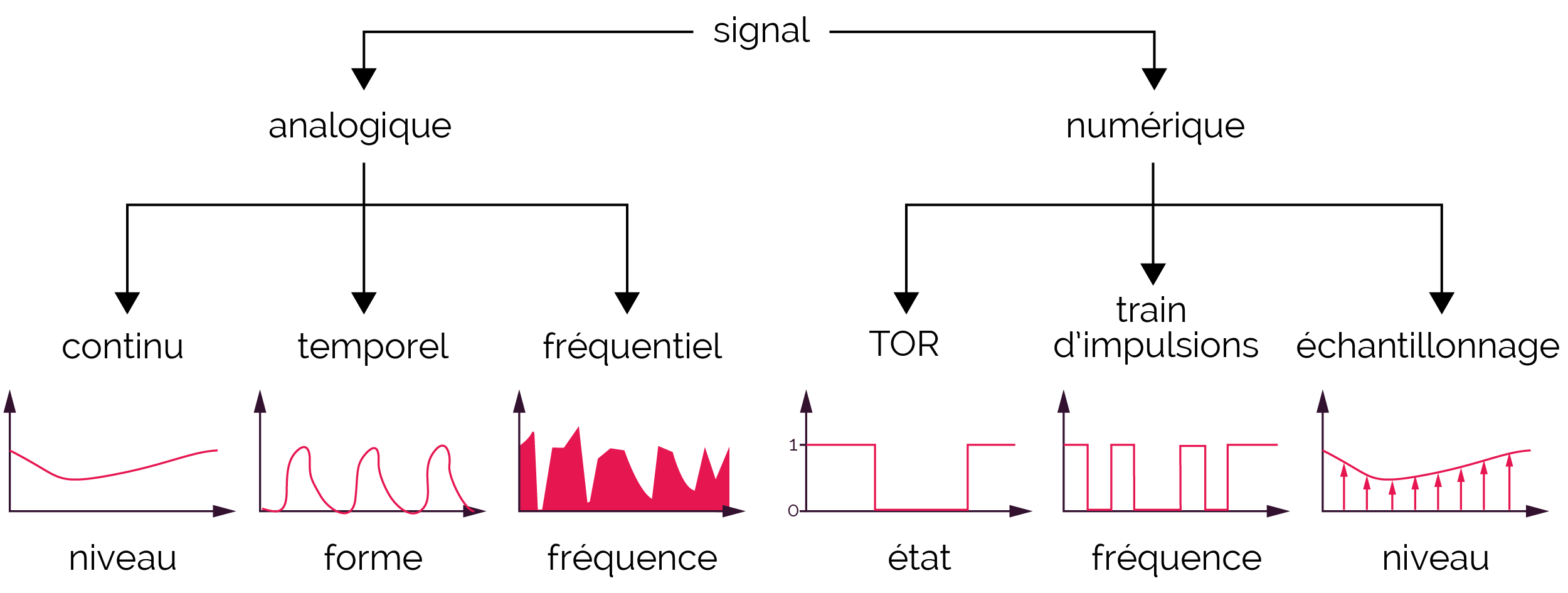
Les signaux électriques
- Un signal continu est un signal dont la variation
est relativement lente, l’information utile est
l’évolution de la grandeur dans le temps.
Exemples : température, débit
- Un signal temporel est un signal
caractérisé par sa forme, en
général cyclique (périodique).
Exemples : pression cardiaque, courant alternatif
- Un signal fréquentiel est un signal dont
l’information utile est donnée par le
spectre fréquentiel.
Exemples : analyse vocale, sonar
- Un signal TOR est un signal à deux
états stables qui représentent
l’état d’un organe.
Exemples : vanne ouverte ou fermée, fin de course activée ou non
- Un train d’impulsions est un signal à
deux états stables dont les changements
d’état dans le temps constituent
l’information utile.
Exemple : codeur incrémental
- Un échantillonnage est une image
numérique d’un signal analogique,
constituée d’échantillons
prélevés à période
constante.
Exemple : son digital
Un signal analogique peut être régulier, on dit qu’il est périodique. Le signal présente alors un motif élémentaire : une partie de la courbe se répète à intervalles de temps réguliers.
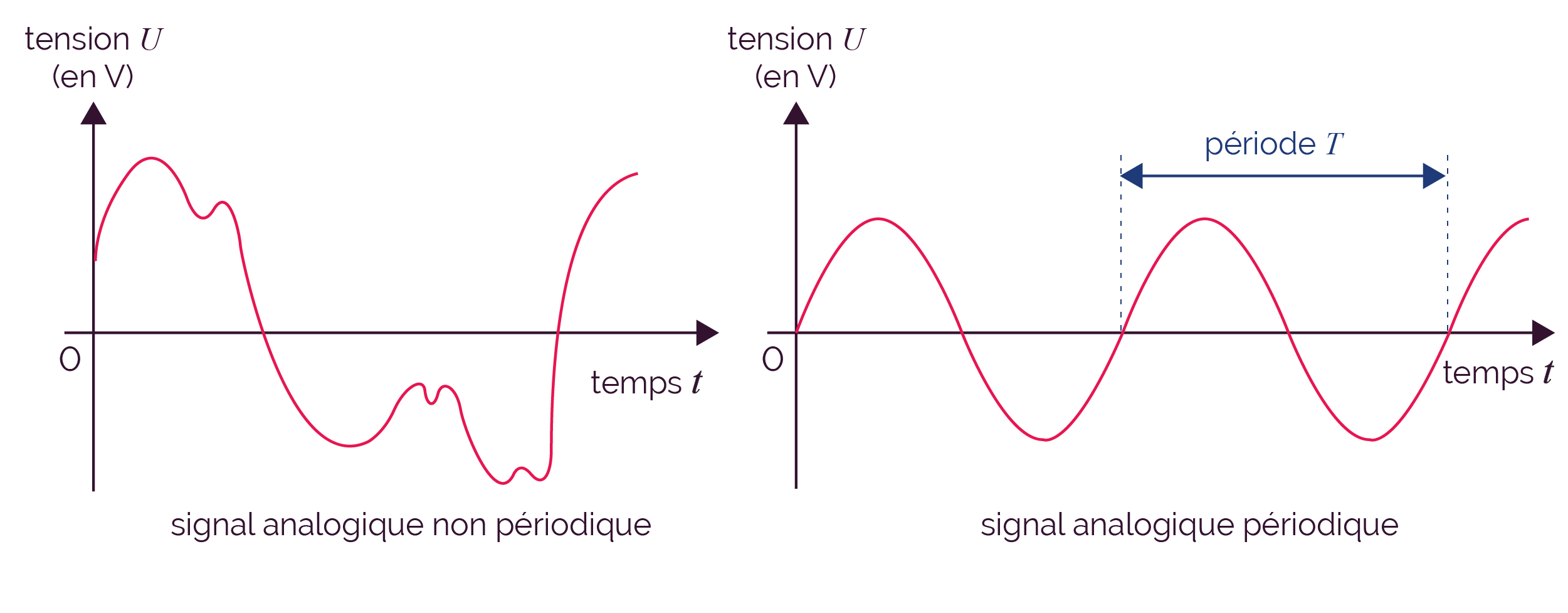
Le signal analogique périodique le plus courant est le signal sinusoïdal.
On peut déterminer la période et la fréquence d’un signal analogique périodique.
La période peut être lue comme étant la durée entre deux « sommets » de la courbe.
La fréquence f est l’inverse de la période T.
On a ainsi la relation suivante.
|
|
avec :
|
Plus un signal possède une période courte (donc un motif de durée courte), plus le motif élémentaire se répète pendant une seconde, ce qui implique une fréquence plus élevée.
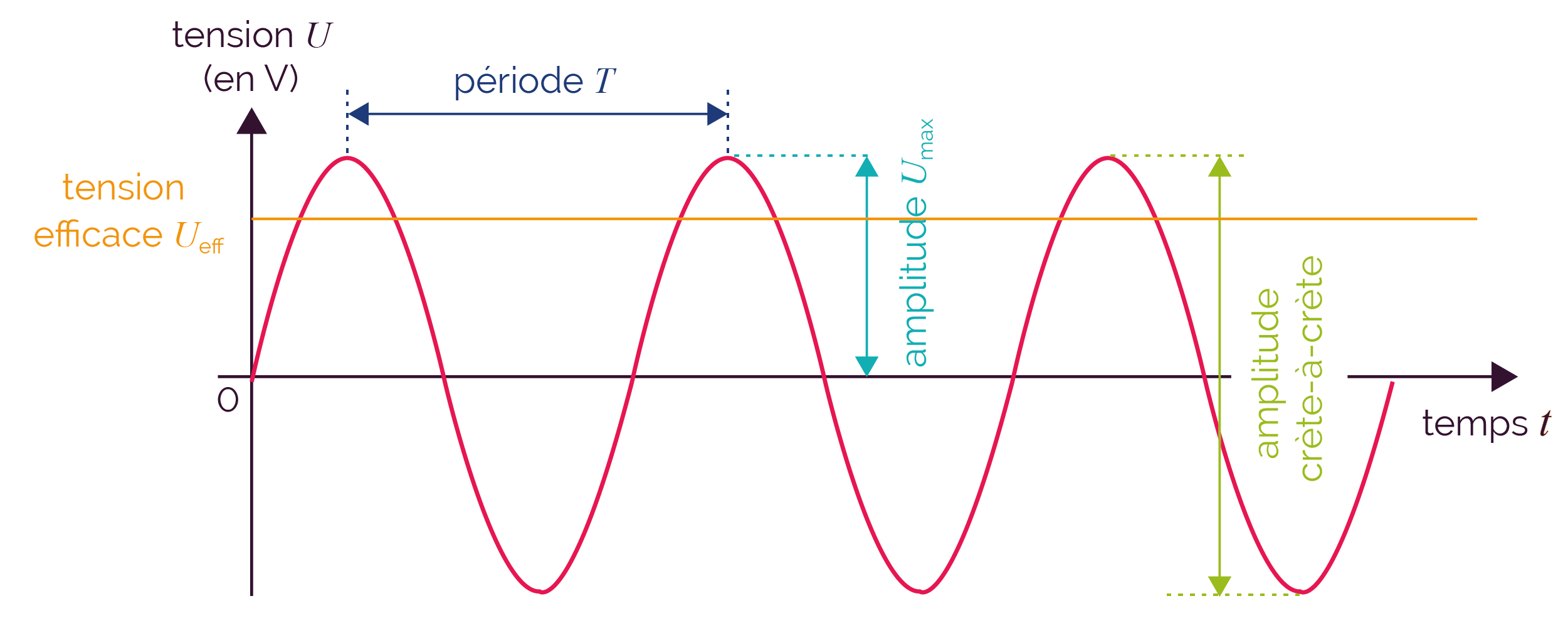
On peut déterminer l’amplitude, l’amplitude crête-à-crête et la tension efficace d’un signal analogique périodique.
La tension d’un signal sinusoïdal varie entre une valeur maximale Umax et une valeur minimale.
La valeur maximale Umax correspond à l’amplitude du signal et la différence entre les valeurs maximale et minimale correspond à l’amplitude crête-à-crête.
La tension efficace Ueff
d’une tension alternative sinusoïdale est la
valeur mesurée par un voltmètre. La
tension efficace s’exprime en volt (V) et se
calcule en divisant la valeur de la tension maximale
par une constante ![]() .
.
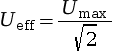
|
avec :
|
On distingue deux niveaux dans un signal numérique :
- un niveau haut : H (High), NL1, 1 ;
- un niveau bas : L (Low), NL0, 0.
On utilise un chronogramme pour représenter ces signaux.
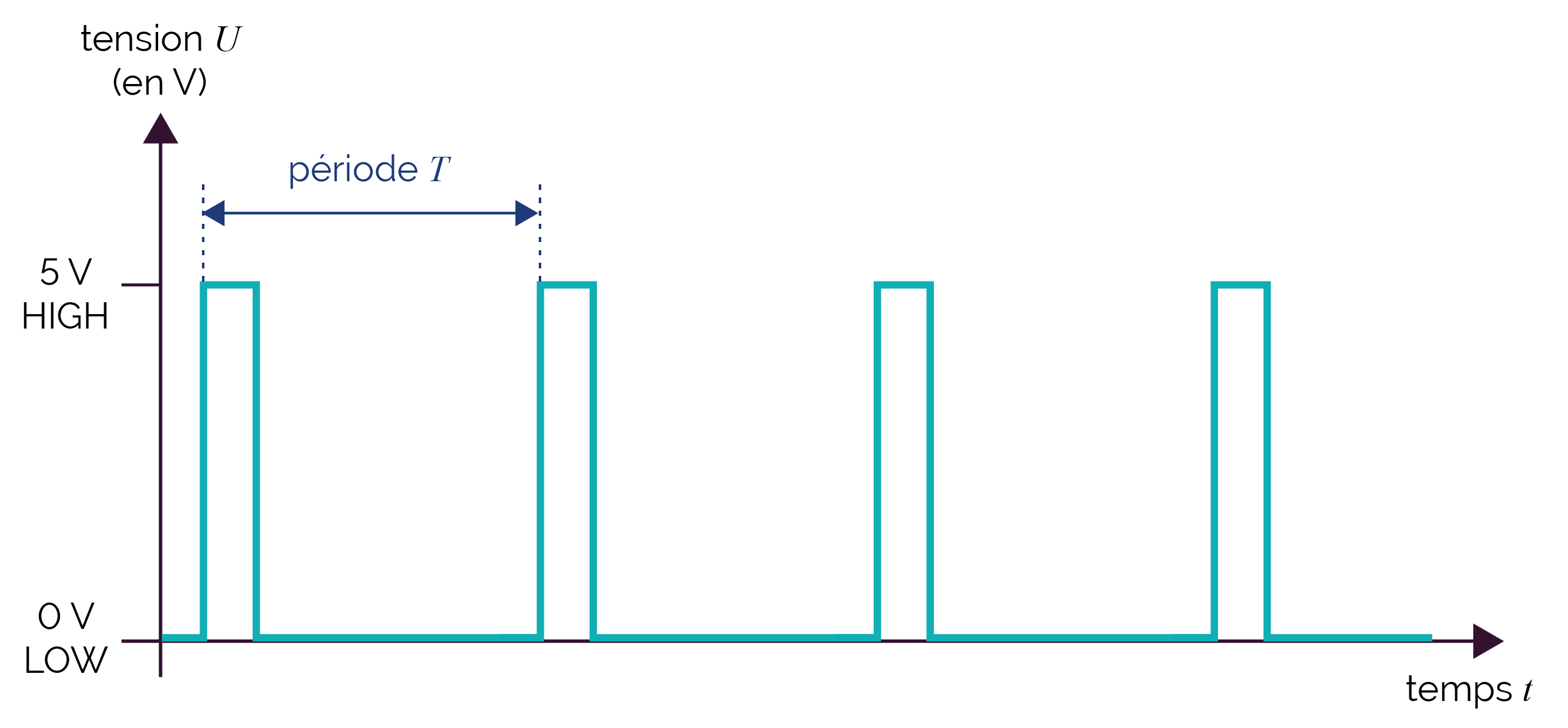
Le train d’impulsions est un signal logique qui a deux états stables, dont les changements d’état dans le temps constituent l’information utile (par exemple un codeur incrémental).
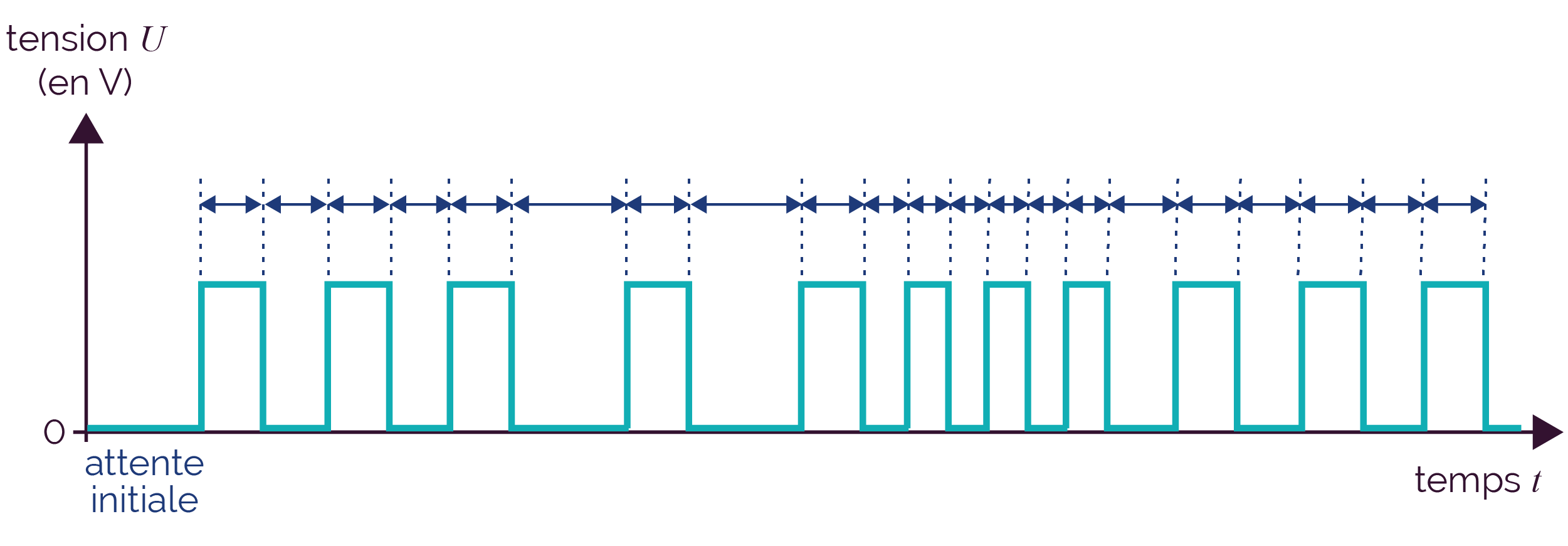
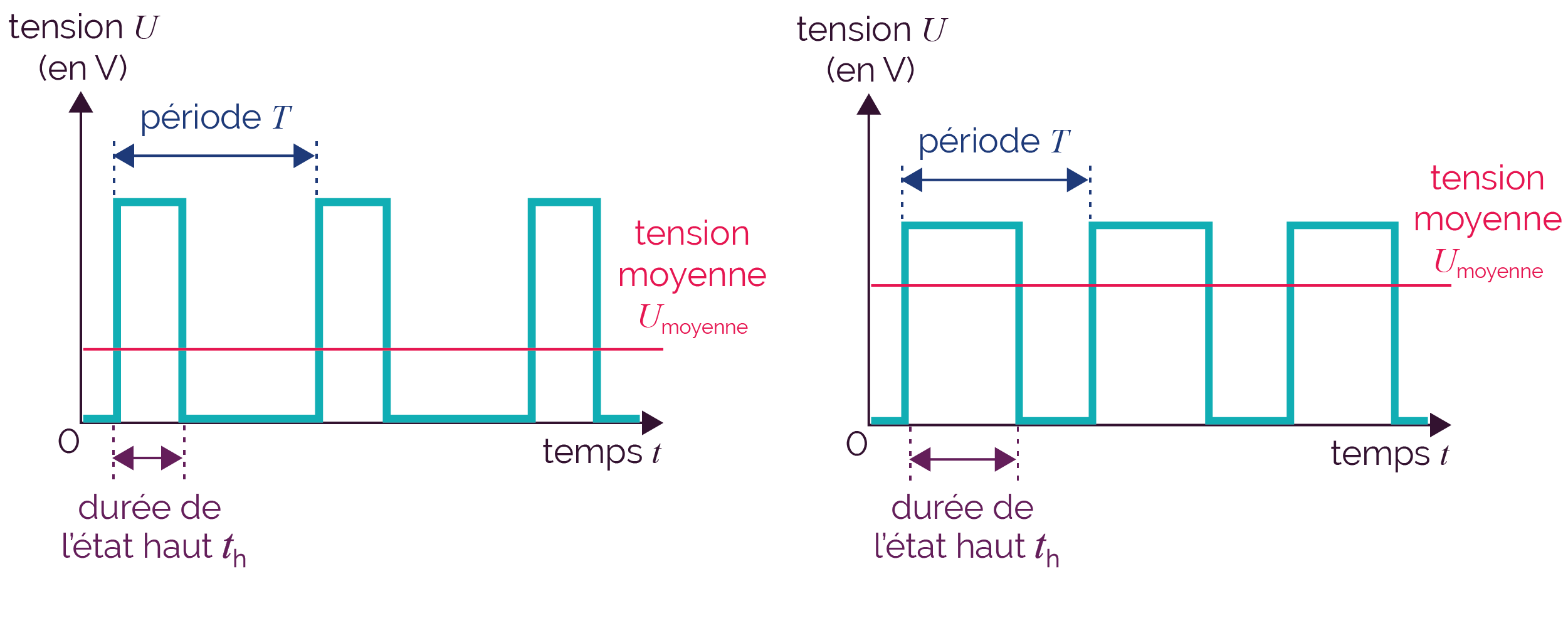
L’information utile est le temps au niveau haut
par rapport à la période.
L'information est caractérisée par le
rapport cyclique.
|
|
avec :
|
Le rapport cyclique α est compris
entre 0 et 1 mais est souvent exprimé
en pourcentage (si α = 0,2 alors
α = 20 %).
Si α = 0, la
tension moyenne est nulle et si α = 1 la
tension moyenne correspond à la valeur maximale.
On peut calculer la tension moyenne Umoyenne d’un signal périodique rectangulaire en utilisant le rapport cyclique.
![]() donc
donc ![]()

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









