La résistance des matériaux
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Comprendre les objectifs de l’étude de la résistance des matériaux.
- Connaitre les caractéristiques des sollicitations simples.
- Découvrir les apports de la modélisation par éléments finis.
- Un matériau est soumis à des efforts extérieurs divers, qui ont des caractéristiques différentes : traction, compression, flexion, cisaillement ou torsion.
- Une contrainte σ subie par le
matériau représente une pression interne dans
le matériau suite à l’un de ces efforts
extérieurs :
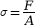avec F la force
exercée sur le matériau et A l’aire de la
surface.
- Lorsque l’on applique une contrainte sur une pièce, celle-ci commence par se déformer de façon élastique (déformation réversible) jusqu’à ce que le niveau de contraintes atteigne la limite élastique Re du matériau. Passé ce seuil, si on continue à augmenter l’intensité de l’effort appliqué, la pièce se déforme de façon irréversible (déformation plastique) et ce, jusqu’à la rupture de la pièce.
- Le module d’élasticité longitudinale E (ou module de Young) caractérise l’élasticité du matériau : σ = E × ε avec σ la contrainte et ε l’allongement relatif.
- Un matériau résiste si la contrainte
maximale σmax ne dépasse
pas la limite élastique Re du
matériau :
,
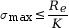avec Re la limite élastique
et K un
coefficient de sécurité.
L’étude de la résistance des matériaux a trois objectifs principaux.
- La connaissance des caractéristiques mécaniques des matériaux (comportement sous l’effet d’une action mécanique).
- L’étude de la résistance des pièces mécaniques.
- L’étude de la déformation des pièces mécaniques.
Ces études permettent de choisir le matériau et les dimensions d’une pièce mécanique en fonction des conditions de déformation et de résistance requises.
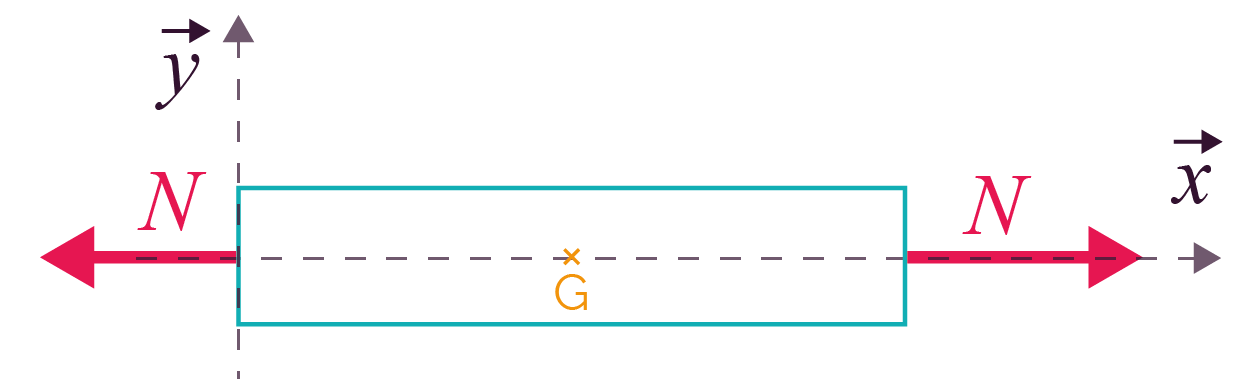
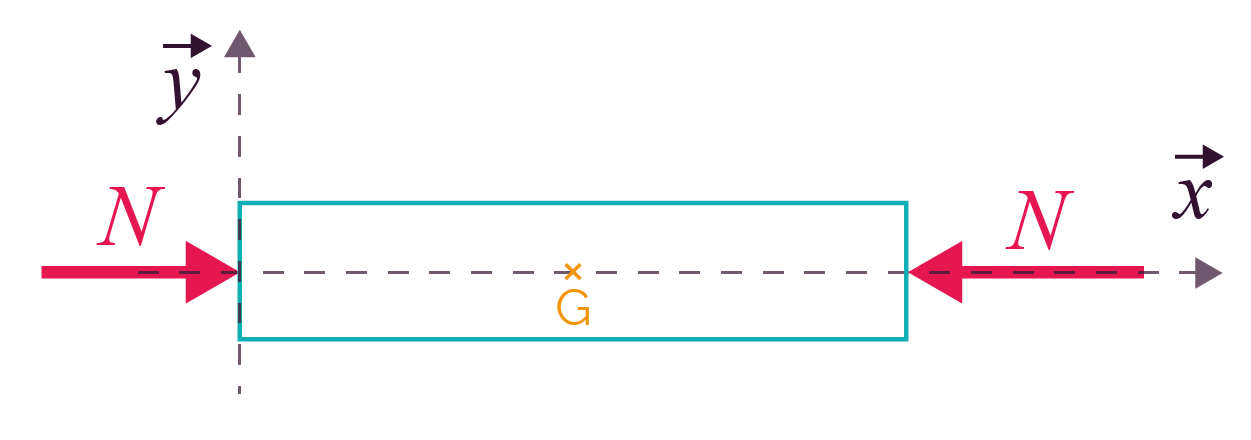
Lorsqu’une pièce est soumise à des efforts extérieurs, pour mettre en évidence les efforts transmis par la matière, on effectue une coupure imaginaire par un plan perpendiculaire à la ligne moyenne de la pièce.
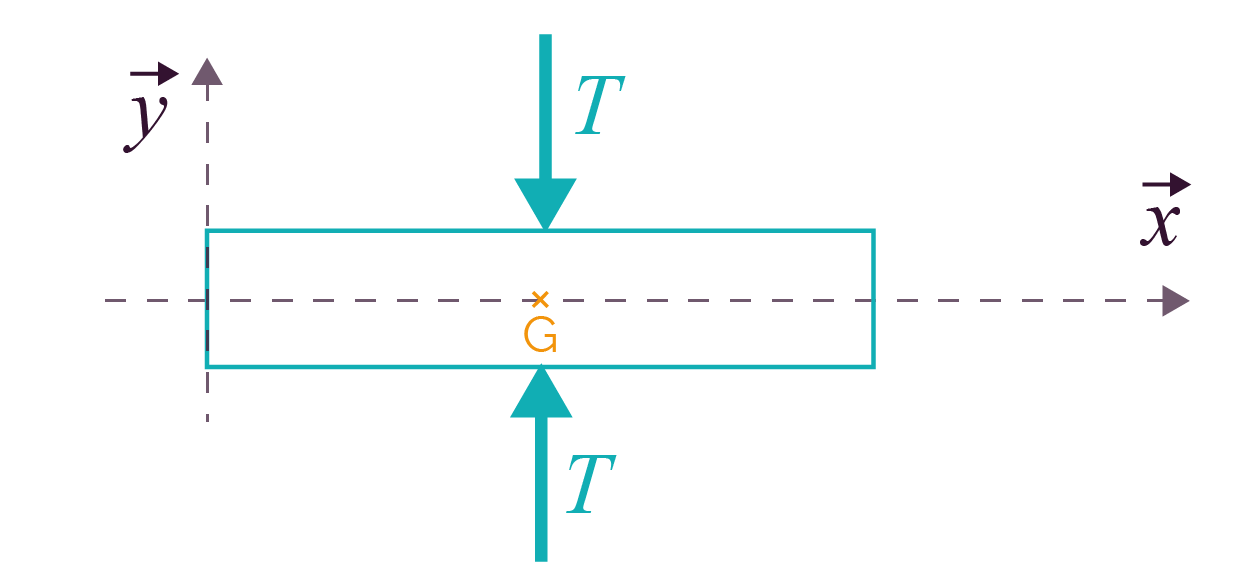
L’identification des efforts intérieurs exercés entre les deux tronçons au niveau de la coupure permet d’écrire le torseur de cohésion.
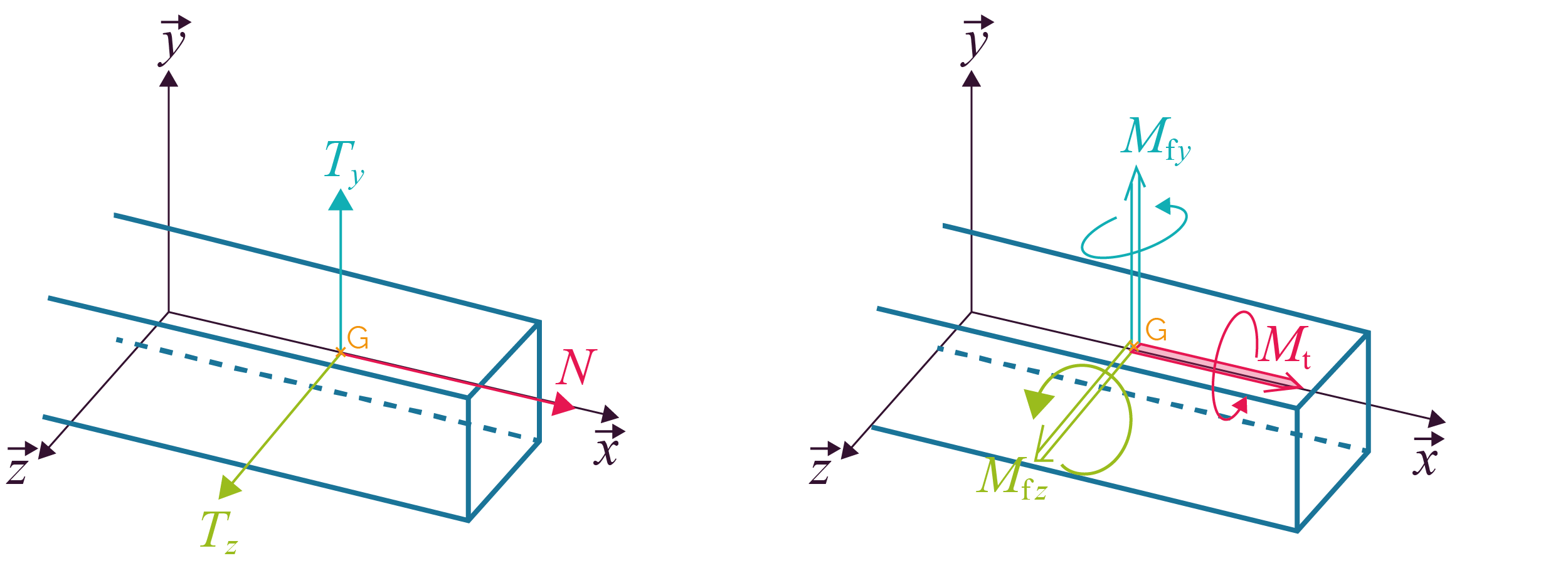
Dans le cas d'une poutre d'axe 
dans un repère
R
(
, 
, 
), ce torseur s'écrit de la manière
suivante au point G.
|
|
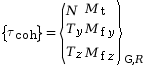
avec :
|
Le tableau suivant liste les différents efforts extérieurs possibles, avec le torseur de cohésion associé.
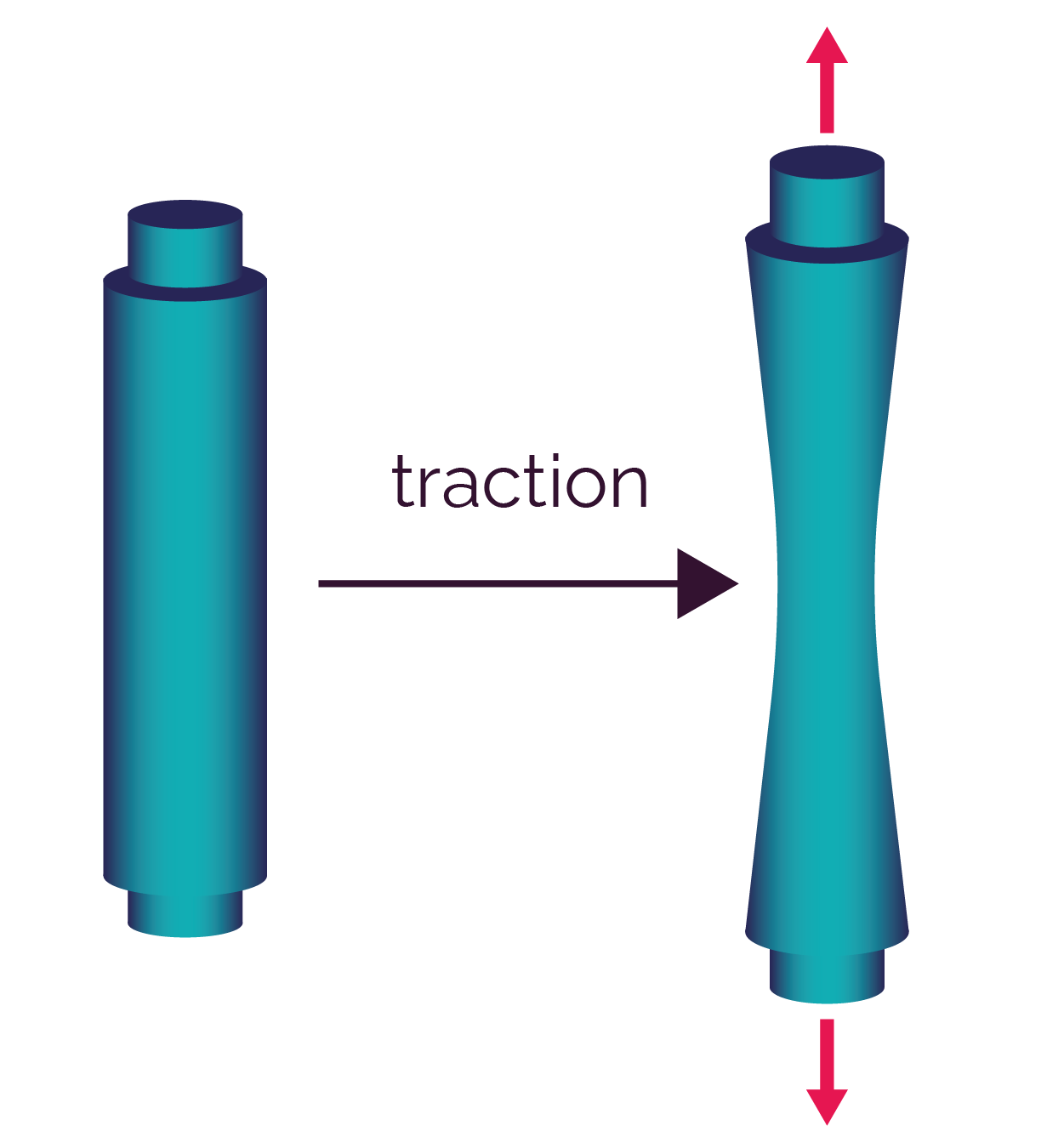
| La traction provoque un allongement qui peut entrainer la rupture du matériau. |
|
 |
|
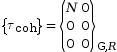
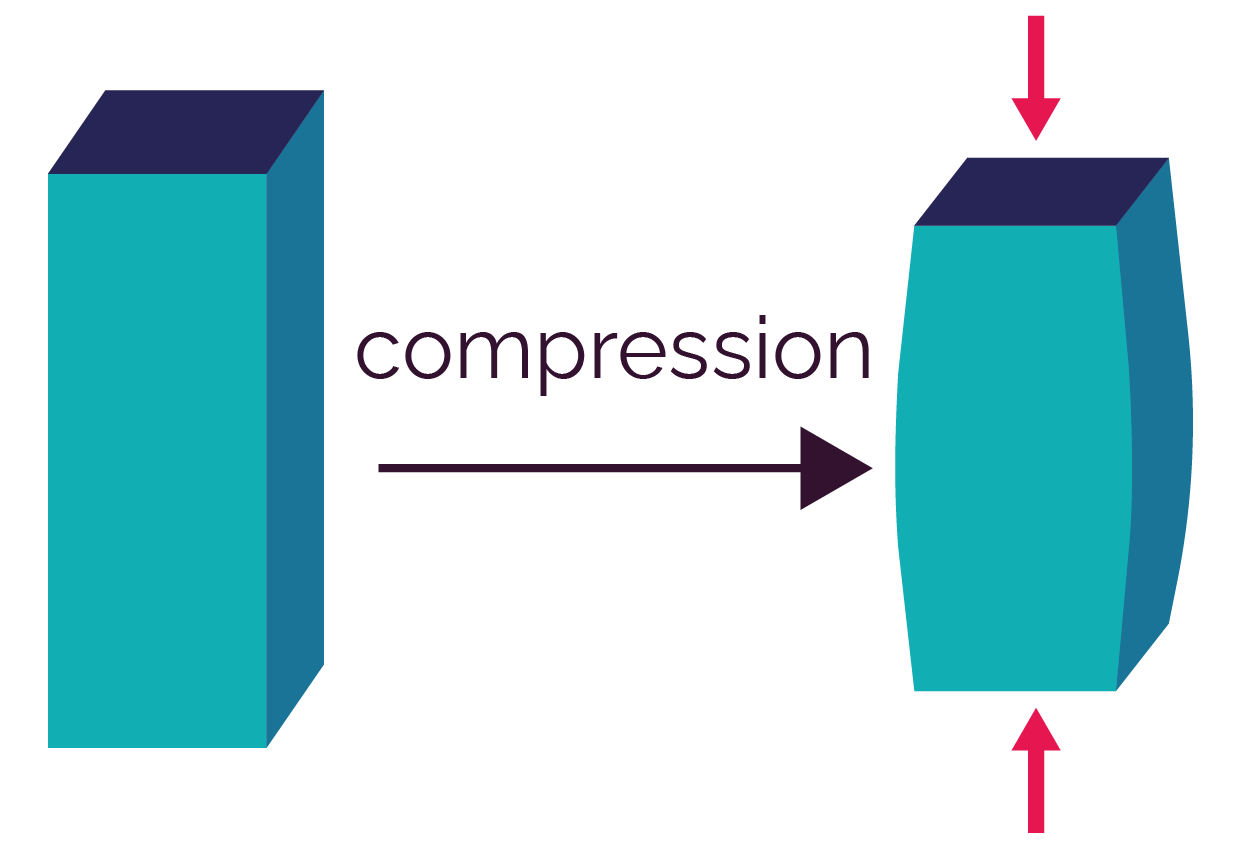
| La compression provoque un raccourcissement qui peut entrainer une pulvérisation du matériau ou un phénomène de flambage. |
|
|
|
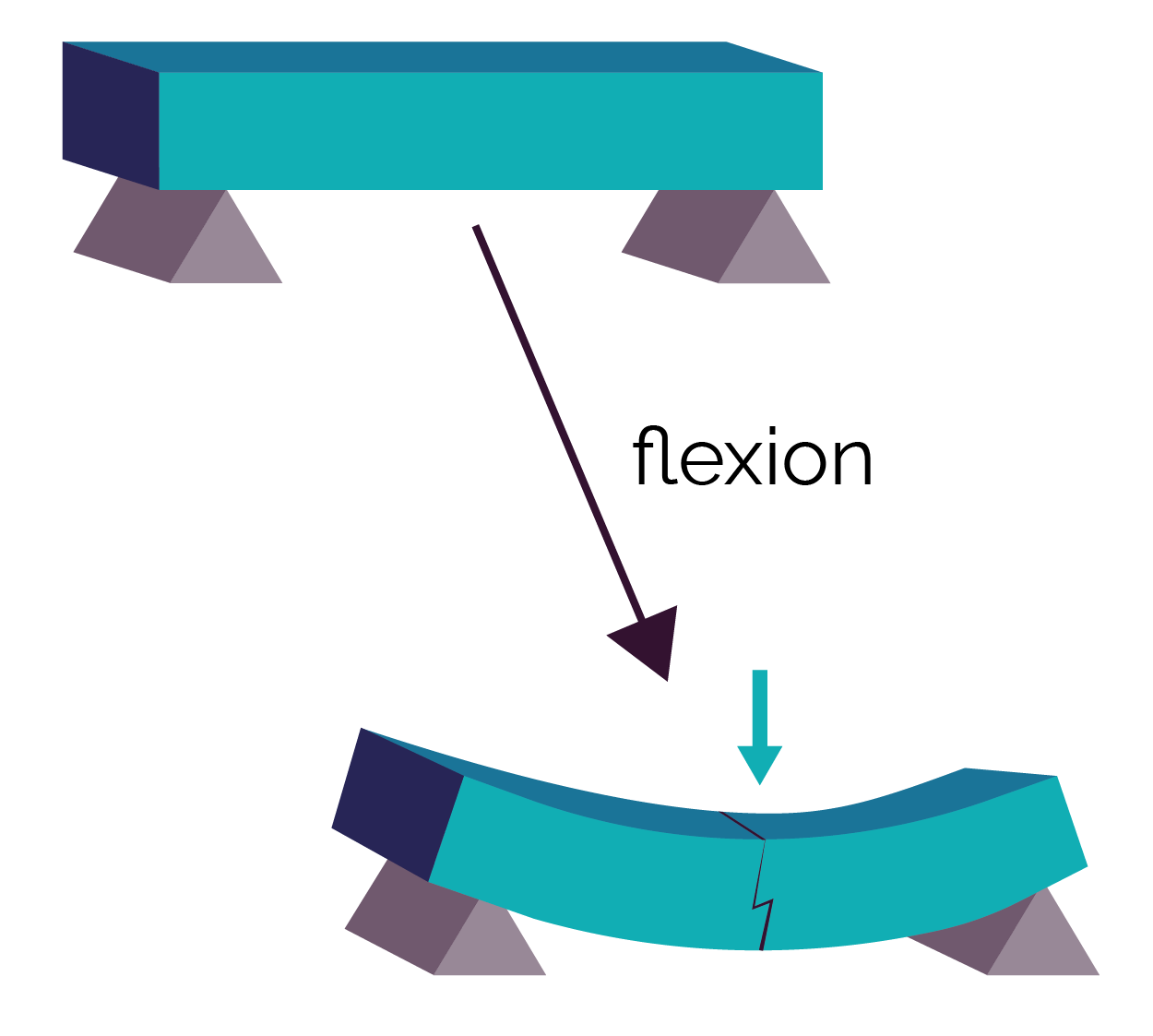
| La flexion provoque un fléchissement qui peut entrainer la rupture du matériau. |
|
 |
|
|
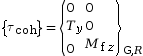
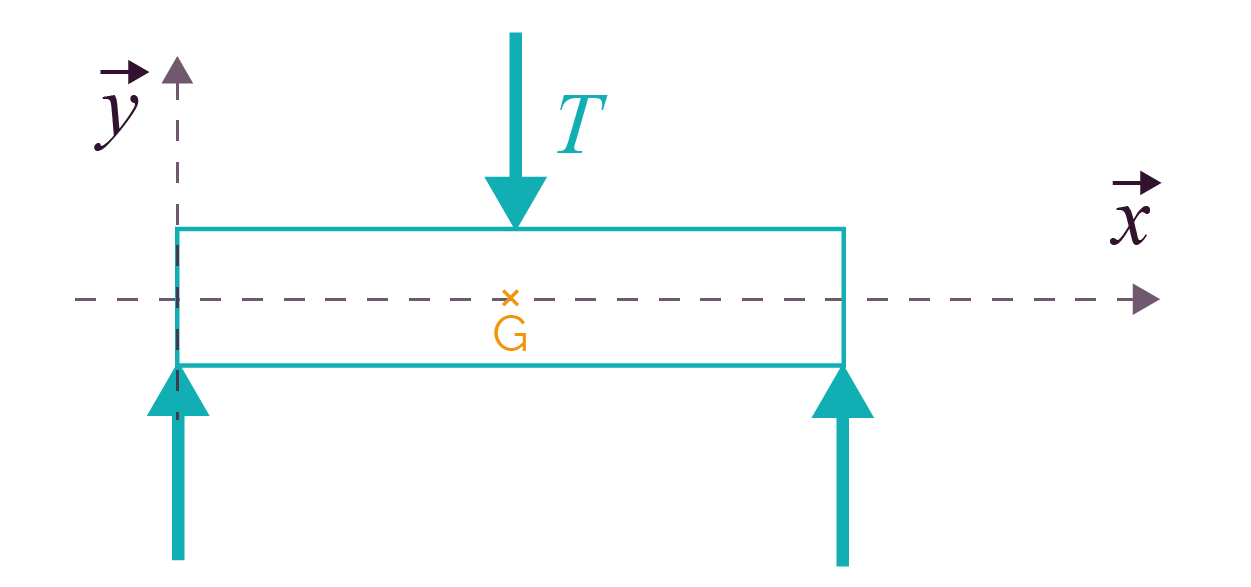
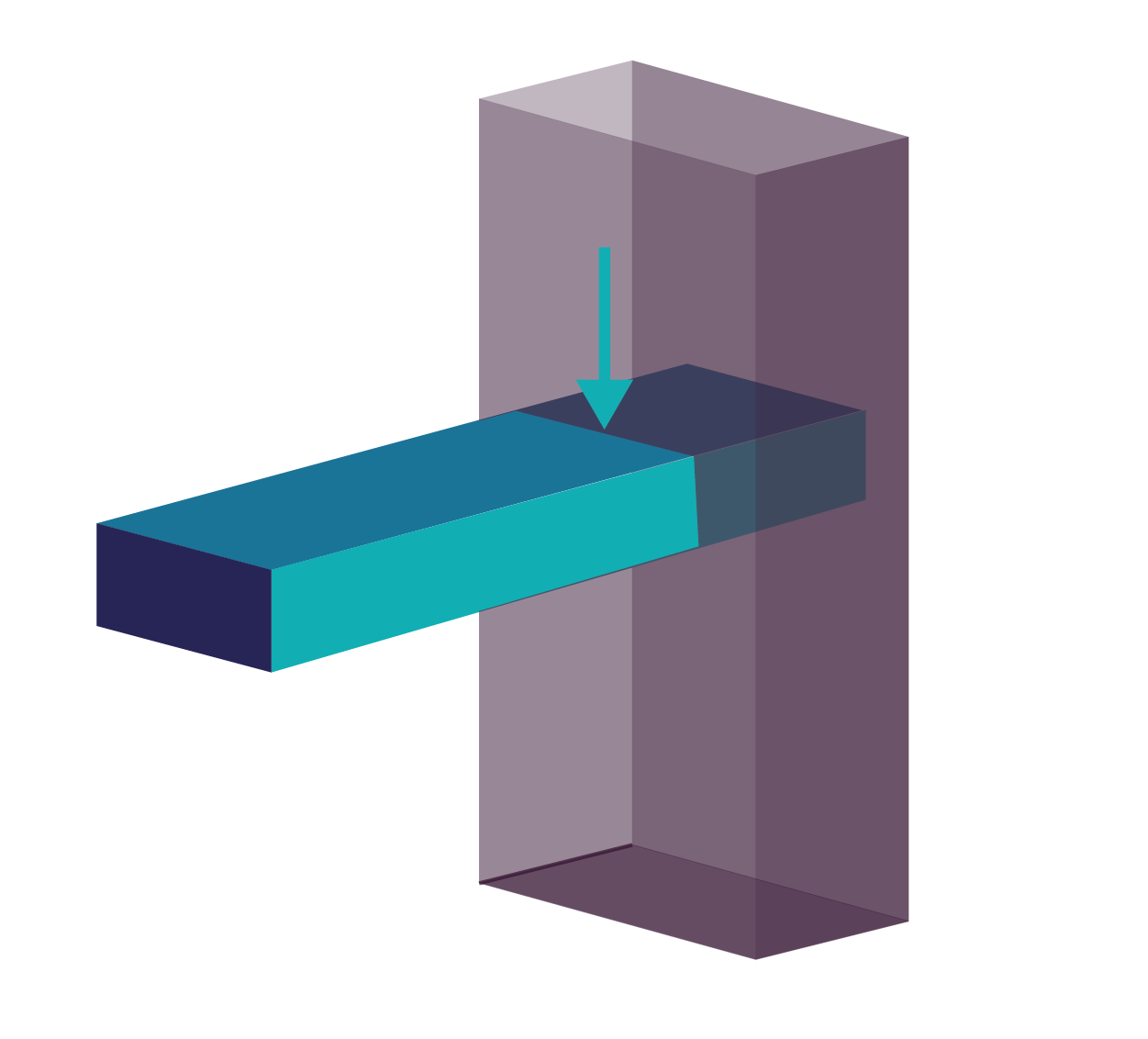
Le cisaillement est souvent rencontré quand il y a des porte-à-faux. Une installation est dite en porte-à-faux lorsqu’un élément est soutenu par un élément qui est lui-même au-dessus du vide, un balcon par exemple. Le cisaillement provoque une fissure qui peut entrainer la rupture du matériau. |
|
 |
|
| La torsion est souvent rencontrée sur les arbres de transmission. |
|
 |
|
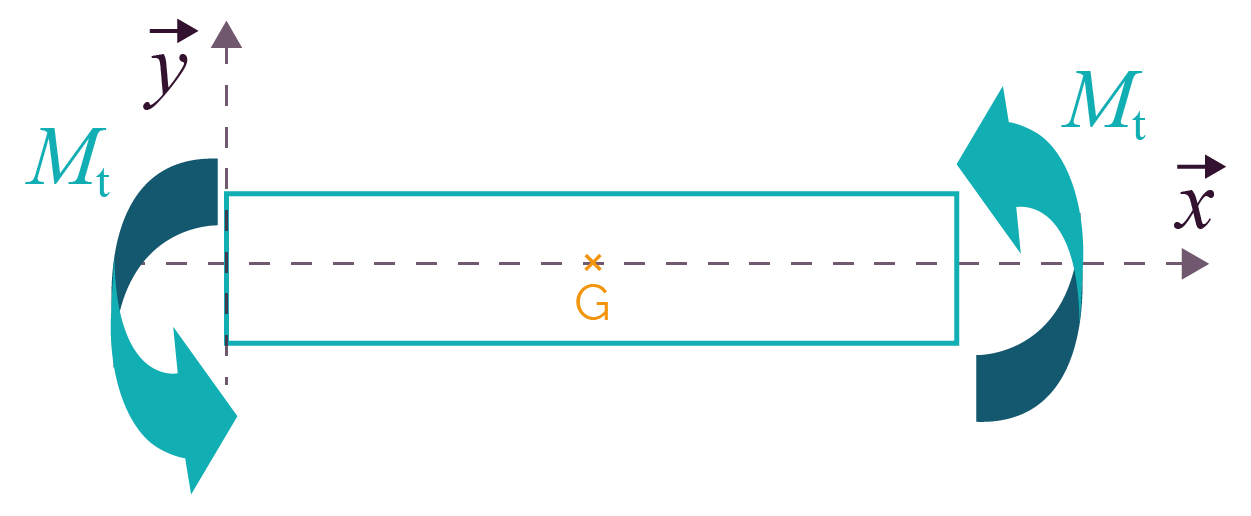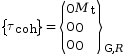
Pour mener des études de résistance des matériaux, il est nécessaire de poser des hypothèses sur le matériau.
Les hypothèses posées sont souvent les suivantes.
- Le matériau est isotrope : il possède les mêmes propriétés mécaniques dans toutes les directions. Cette propriété n’est pas vérifiée pour les matériaux tels que le bois, les matériaux composites, etc.
- Le matériau est homogène : il a la même composition en tout point.
- Le matériau est continu : il ne présente pas de fissures.
Les caractéristiques des différents matériaux sont définies à partir d’essais. Le plus classique est l’essai de traction qui permet d’établir, pour le matériau testé, la courbe de l’évolution de la déformation en fonction des contraintes appliquées à la pièce.
Lorsque l’on applique une contrainte σ sur une pièce, celle-ci commence par se déformer de manière réversible (déformation élastique), c’est-à-dire que ses dimensions changent mais que la pièce reprend sa forme initiale lorsque la sollicitation s’arrête.
Pour les matériaux dits ductiles, c’est-à-dire qui ont la capacité de se déformer sans se rompre, on déforme de manière définitive la pièce lorsque l’on augmente la sollicitation (déformation plastique). Lorsque l’on arrête la sollicitation, la pièce reste déformée.
La longévité et le bon fonctionnement des mécanismes imposent que les pièces restent dans le domaine élastique.
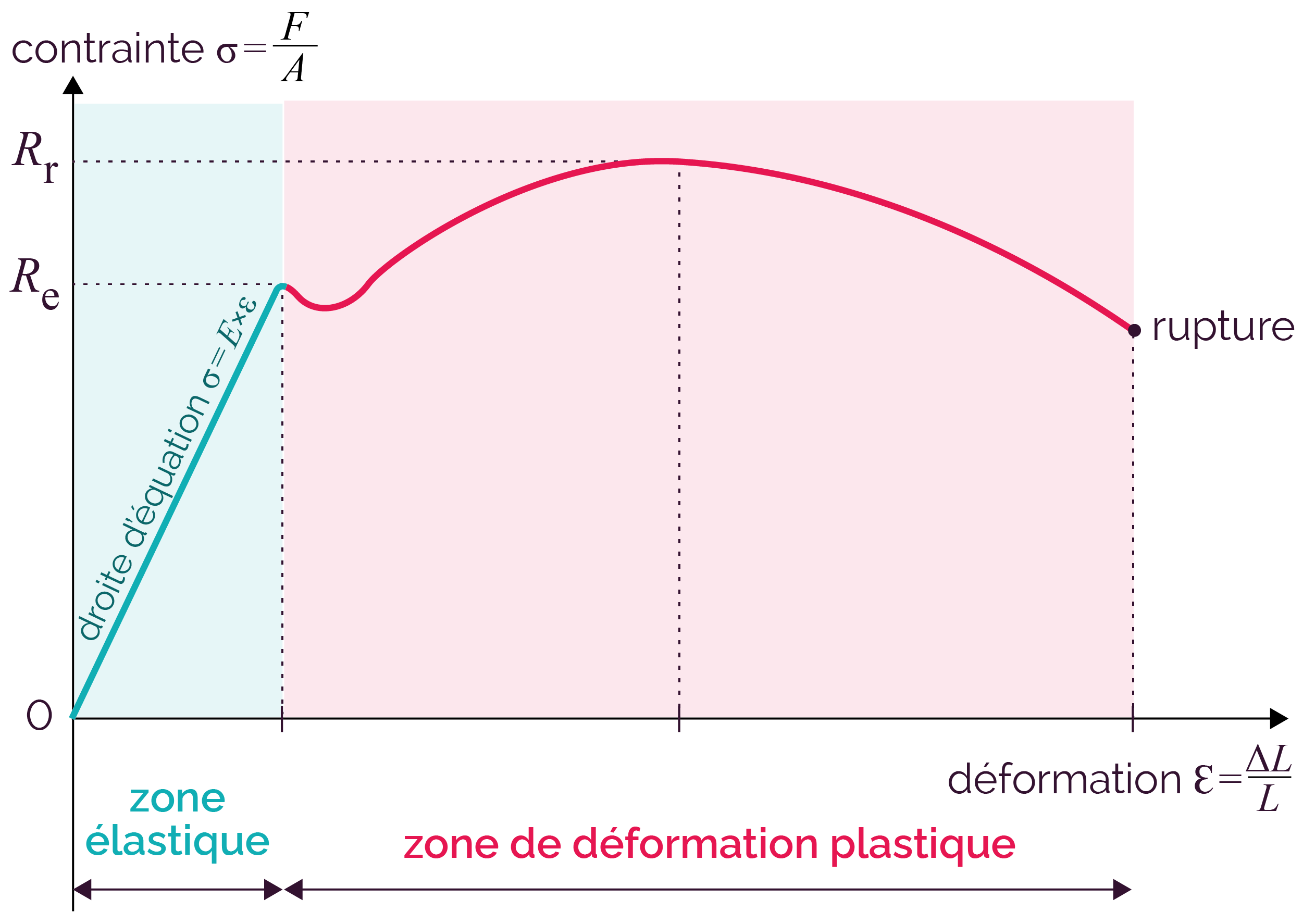
Diagramme contrainte-déformation
Sur le visuel ci-dessus :
- la limite à la rupture Rr correspond à la contrainte maximale atteinte au cours de l’essai ;
- la limite élastique Re marque la fin du domaine élastique. Au-delà de cette valeur, la pièce se déforme plastiquement.
Le module d’élasticité longitudinale E (ou module de Young) caractérise l’élasticité du matériau et correspond à la pente de la courbe dans le domaine élastique.
Plus E est grand et plus le matériau est rigide (et inversement).
- Eacier = 200 000 N/mm2
- Ecaoutchouc = 7,5 N/mm2
La loi de Hooke traduit ce principe.
| σ = E × ε |
|
avec :
|
avec :
avec :
Pour tenir compte des incertitudes liées au matériau, à la simulation, à l’intensité des efforts, on applique fréquemment un coefficient de sécurité K.
|
avec :
|
Pour calculer le coefficient de sécurité
pour une pièce pour laquelle on connait
l’intensité maximale des contraintes, on
applique la formule 
.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Sciences de l’ingénieur
Utiliser les torseurs
Sciences de l’ingénieur
Les réseaux informatiques
Sciences de l’ingénieur
Travailler en équipe - lycée
Sciences de l’ingénieur
Constituer un dossier documentaire - Sciences de l'ingénieur
Sciences de l’ingénieur
Simuler à partir d'un modèle donné
Sciences de l’ingénieur
Mettre au point un protocole expérimental
Sciences de l’ingénieur
Afficher une droite de régression et son équation dans Excel
Sciences de l’ingénieur
Les grandes familles de capteurs
Sciences de l’ingénieur
Construire un arbre de décision
Sciences de l’ingénieur
Réaliser une analyse multicritère
Sciences de l’ingénieur
Le contrôle et l'évaluation de la recherche
Fermer
Accédez gratuitement à
