Utiliser les torseurs
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Savoir lire et écrire un torseur.
- Apprendre à effectuer les calculs et opérations courantes sur les torseurs.
- Connaitre une méthode de résolution de problème qui implique les torseurs.
- Un torseur est un outil mathématique qui aide à la résolution de problèmes de mécanique.
- Un torseur est lié à un point et il
comporte deux vecteurs, la résultante et le
moment :
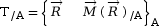
- Certains torseurs sont particuliers : le torseur nul, le glisseur et le couple.
- Plusieurs torseurs peuvent être additionnés.
- Pour changer le point par rapport auquel un torseur est
exprimé :
- on conserve la résultante ;
- on modifie le moment grâce à la
relation de Varignon :
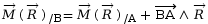 .
.
- Action mécanique
- Vecteur
En mécanique du solide indéformable, le torseur permet de simplifier la résolution de nombreux problèmes, dans un plan (2D) comme dans l’espace (3D). C’est le cas des problèmes liés à la transmission d’actions mécaniques, au déplacement, à la vitesse ou à l’accélération d’un solide.
En mécanique du solide, les corps étudiés (produit, assemblage ou pièce) sont modélisés par des solides (objets tridimensionnels). Au lycée, on considère que les solides sont indéformables lorsqu’on utilise les torseurs (les torseurs ne sont pas utilisables avec des solides déformables).
Le torseur statique permet de modéliser la manière dont les efforts sont transmis entre plusieurs solides dans un assemblage à l’équilibre statique (qui n’est pas en mouvement).
À partir de quelques données sur la situation étudiée, le torseur statique permet de déterminer toutes les inconnues du problème en résolvant quelques équations.
Voici la forme générale d’un torseur, exprimé au point A.
|
|
Un torseur est composé de deux vecteurs.
|
- La résultante résume l’action de poussée ou de traction qui résulte d’une action mécanique appliquée sur un solide.
- Le moment représente la manière dont l’action mécanique a tendance à faire tourner le solide autour d’un axe.
- La résultante du torseur est invariable : peu importe le point du plan ou de l'espace utilisé pour écrire le torseur, elle est toujours la même.
- Le moment dépend du point du torseur : le moment est différent si on change le point d’écriture du torseur.
Soit une voiture qui est en contact avec le sol en A.
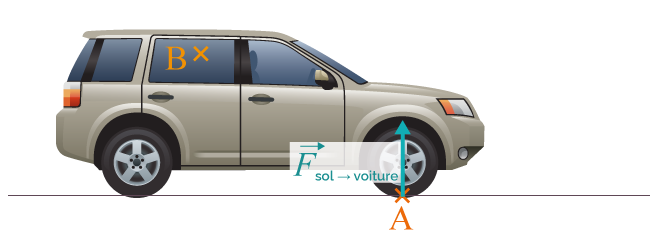
On utilise pour cela le torseur suivant.
Comme les deux éléments qui composent le torseur sont des vecteurs, on peut aussi écrire un torseur sous sa forme décomposée.
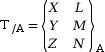
|
avec :
|
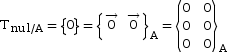
Le torseur nul est invariable, peu importe le point utilisé pour exprimer le torseur.
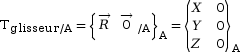
Bien que le moment soit nul au niveau du point où le glisseur est exprimé, ce n’est pas le cas par rapport à tous les points du plan/espace. En changeant le point à partir duquel on exprime le torseur, un moment peut apparaitre.
Un torseur glisseur est produit par une action mécanique qui « pousse » ou « tire » le solide qui la subit.
Le nom glisseur vient du fait que le torseur fait simplement « glisser » (« pousse » ou « tire ») le solide sans le faire tourner.
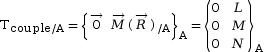
Un torseur couple est produit par une action mécanique qui ne tend qu’à mettre en rotation le solide qui la subit.
- La résultante est invariable, la résultante reste donc nulle, peu importe le point du plan/espace par rapport auquel on exprime le torseur.
- Comme un torseur quelconque, le moment d’un couple est variable en fonction du point où le torseur est exprimé.
Il suffit alors d’additionner leurs composantes
une à une.
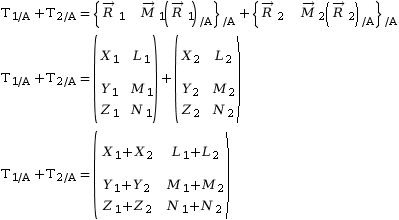
Soit les deux torseurs suivants, exprimés en A.

Il est possible, de la même manière, d’additionner plus de deux torseurs ou de soustraire des torseurs.
Il est nécessaire de savoir s’en servir lorsque l’on manipule des torseurs.
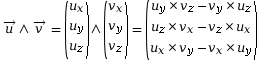
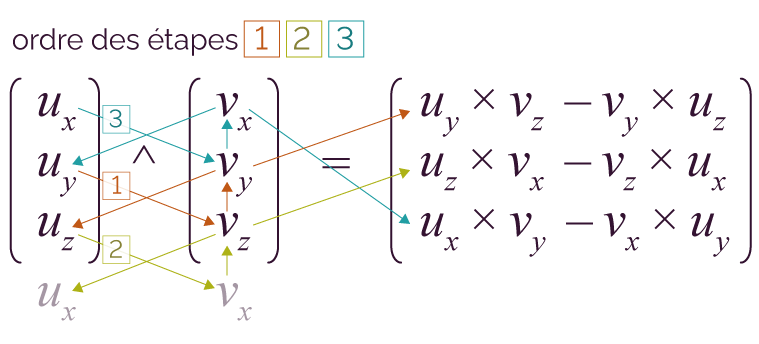
Soient les deux vecteurs
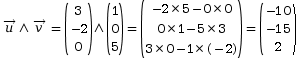
Il est souvent nécessaire de changer le point par rapport auquel un torseur est écrit. C’est notamment le cas lorsqu’on doit additionner des torseurs qui sont au départ exprimés par rapport à des points différents.
- on conserve la résultante telle quelle ;
- on se sert de la relation de Varignon pour déplacer le moment.
La relation de Varignon s’exprime de la manière suivante.
|
|
avec :
|
Soit un torseur T, dont on connait les
composantes au point A.
On veut déterminer ses composantes au
point B.
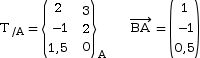
On commence par calculer le moment en B en
appliquant la relation de Varignon, ce qui
donne :
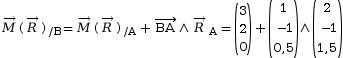
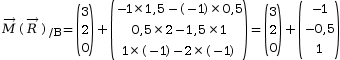
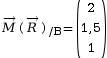
Pour écrire le torseur au
point B, on
associe :
- la résultante qu’on avait pour le torseur au point A ;
- le moment qu’on vient de trouver au point B.
Ce qui donne finalement 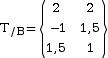 .
.
Un problème qui se sert des torseurs part
toujours d’une égalité.
On essaie dans un premier temps de simplifier au
maximum les deux membres de cette
égalité, afin d’obtenir ensuite une
série d’équations qu’on
résoudra.
Le PFS, principe fondamental de la statique, dit par exemple que la somme des torseurs des actions mécaniques d’un système statique est égale au torseur nul.
Cela donne l’égalité,
Voici les étapes à suivre pour résoudre un problème avec les torseurs, en partant d’une égalité entre les torseurs.
On choisit un point. On déplace ensuite tous les torseurs pour qu’ils soient exprimés en ce point grâce à la relation de Varignon.
On simplifie au maximum les deux membres de l’égalité. Cela revient souvent à additionner tous les torseurs de chaque côté de l’égalité.
On extrait de l’égalité un système d’équations. On se retrouve avec un système d’au maximum 6 équations : une par composante des torseurs.
Plusieurs équations ne sont souvent pas utilisables, ou alors elles s’annulent. On a ainsi seulement 2 ou 3 équations dans le système.
On résout les équations afin de déterminer les valeurs de toutes les inconnues.
On écrit les torseurs en remplaçant les inconnues par leurs valeurs.
On souhaite résoudre un problème qui implique les trois torseurs suivants.
![]()
On connait la plupart de leurs composantes.
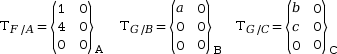
Les résultantes ![]() et
et ![]() comportent des
inconnues : a, b et c.
La résolution du problème consiste
à déterminer les valeurs de ces
inconnues. Les torseurs de ce problème sont
liés par l’égalité :
comportent des
inconnues : a, b et c.
La résolution du problème consiste
à déterminer les valeurs de ces
inconnues. Les torseurs de ce problème sont
liés par l’égalité :
![]()
Cette égalité est donnée au point A, mais elle fonctionne par rapport à n’importe quel autre point. Il faut juste que les trois torseurs soient exprimés par rapport au même point pour qu’elle soit valable.
On donne également les valeurs des vecteurs qui relient les points A, B et C.
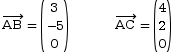
On choisit un point parmi les trois qu’on connait (A, B et C) pour exprimer les trois torseurs. On choisit ici le point A, mais on pourrait aussi bien résoudre le problème avec les deux autres points.
Écriture du torseur TF en A
Ce torseur est déjà écrit
en A, il
n’y a donc pas de transformation à
faire.
Le torseur TF au point A
est 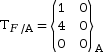
Écriture du torseur TG en A
Comme on ne connait que l’écriture du torseur en B, on se sert de la relation de Varignon pour déplacer le moment en A.
![]()
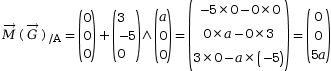
Le torseur TG au
point A est 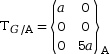 .
.
Écriture du torseur TH en A
Comme on ne connait que l’écriture du torseur en C, on se sert de la relation de Varignon pour déplacer le moment en A.
![]()
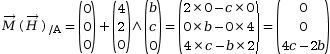
Le torseur TH au
point A
est 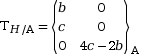
L’équation de départ
est ![]() .
.
On additionne les trois torseurs à gauche de l’équation.
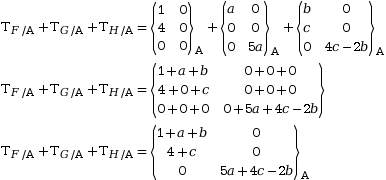
L’équation de
départ, ![]() ,
devient :
,
devient :
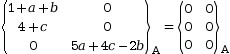
Ce qui donne le système de trois équations suivant.
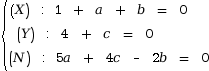
- L’équation (Y) donne immédiatement c = –4
- L’équation (X) peut s’écrire a = –1 – b
- On injecte la valeur de c et l’expression
de a
dans (N) :
5 × (–1 – b) + 4 × (–4) – 2b = 0
–5 – 5b – 16 – 2b = 0
–7b – 21 = 0
–7b = 21
On obtient finalement b = –3. - En reprenant l’équation (X), on a a = –1 – (–3), soit a = 2.
On remplace a, b et c par leurs valeurs, dans les expressions des torseurs.
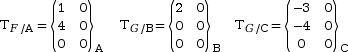

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









