Conditionner des signaux

Le conditionnement permet de mettre en forme le signal mesuré en vue d’un traitement et d’une transmission.

Le conditionnement d’un signal peut être le résultat de plusieurs opérations, comme le montre la chaine d’acquisition ci-dessous.

L’amplification

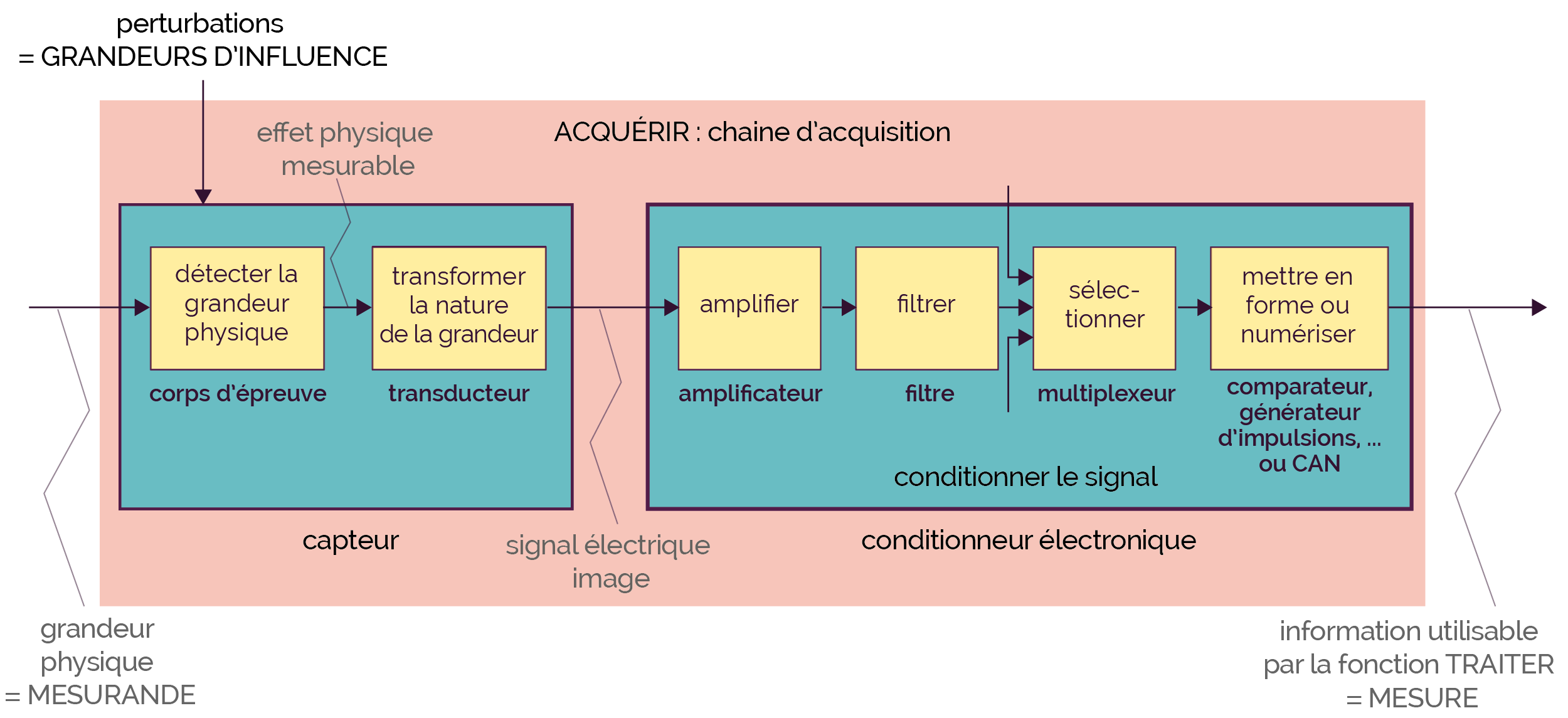
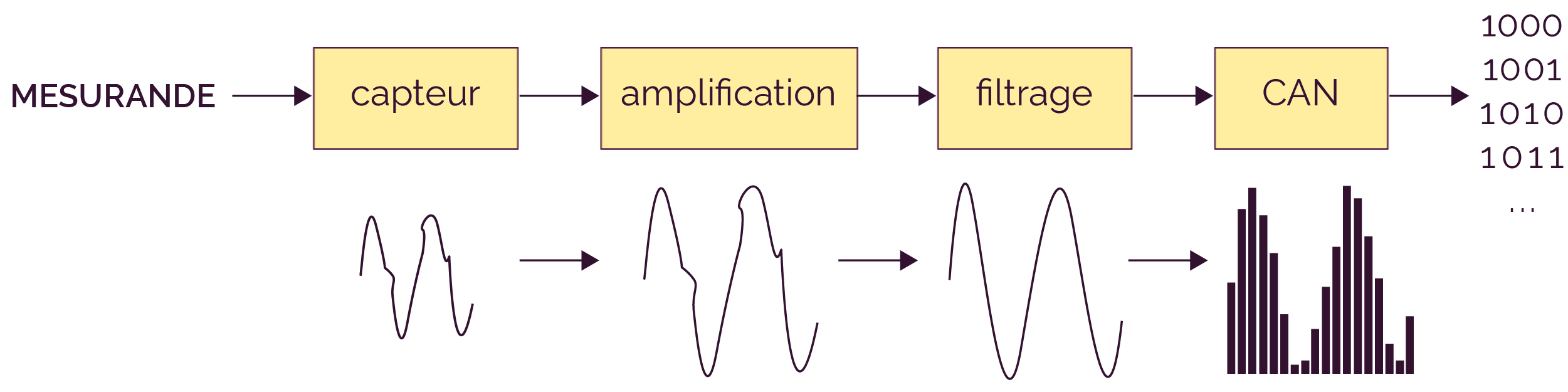
Les amplificateurs élèvent le niveau du signal d'entrée pour mieux correspondre à la gamme du convertisseur analogique/numérique (CAN), ce qui permet d’augmenter la résolution et la sensibilité de la mesure.

L’atténuation

L'atténuation, le contraire de l'amplification, s'impose lorsque les tensions à numériser sont supérieures à la gamme d'entrée du numériseur. Cette forme de conditionnement de signaux diminue l'amplitude du signal d'entrée pour que le signal conditionné se situe dans la gamme d'entrée du CAN. L'atténuation est nécessaire pour les mesures de hautes tensions.

Le multiplexage

En multiplexant, le système de mesure peut router plusieurs signaux de manière séquentielle vers un seul numériseur, ce qui est une manière économique d'augmenter fortement le nombre de voies du système. Le multiplexage est nécessaire pour toute application avec un nombre élevé de voies.

Le filtrage

Les filtres permettent de supprimer certaines fréquences (choisies) d’un signal.

Il est pratique de visualiser les signaux en fonction de la fréquence et non en fonction du temps. C’est ce que l’on appelle le spectre.

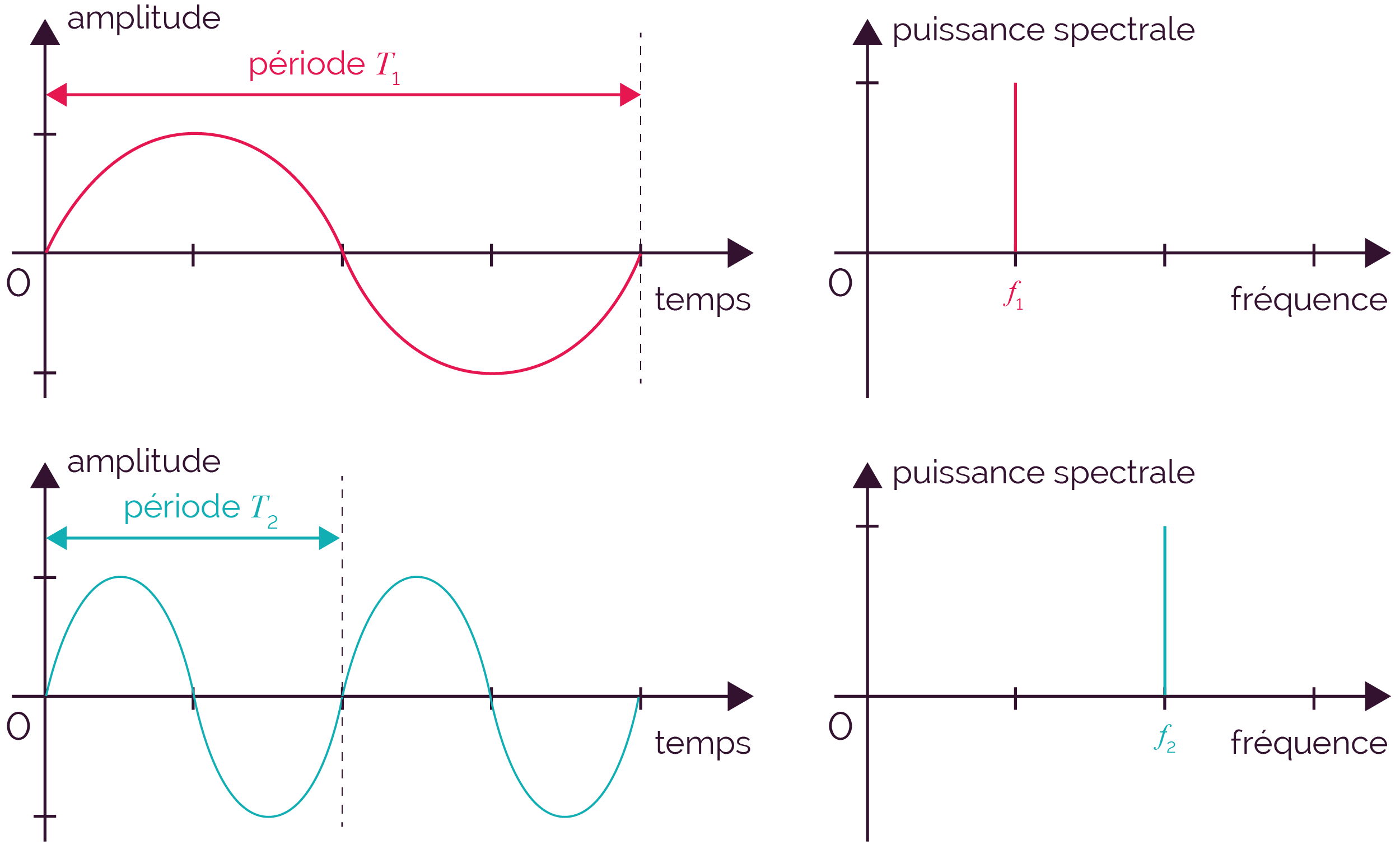
La courbe suivante résulte de la combinaison des deux fonctions précédentes ; elle est donc caractérisée par deux composantes périodiques. L’analyse spectrale permet de retrouver les deux fréquences du signal : f₁ et f₂.

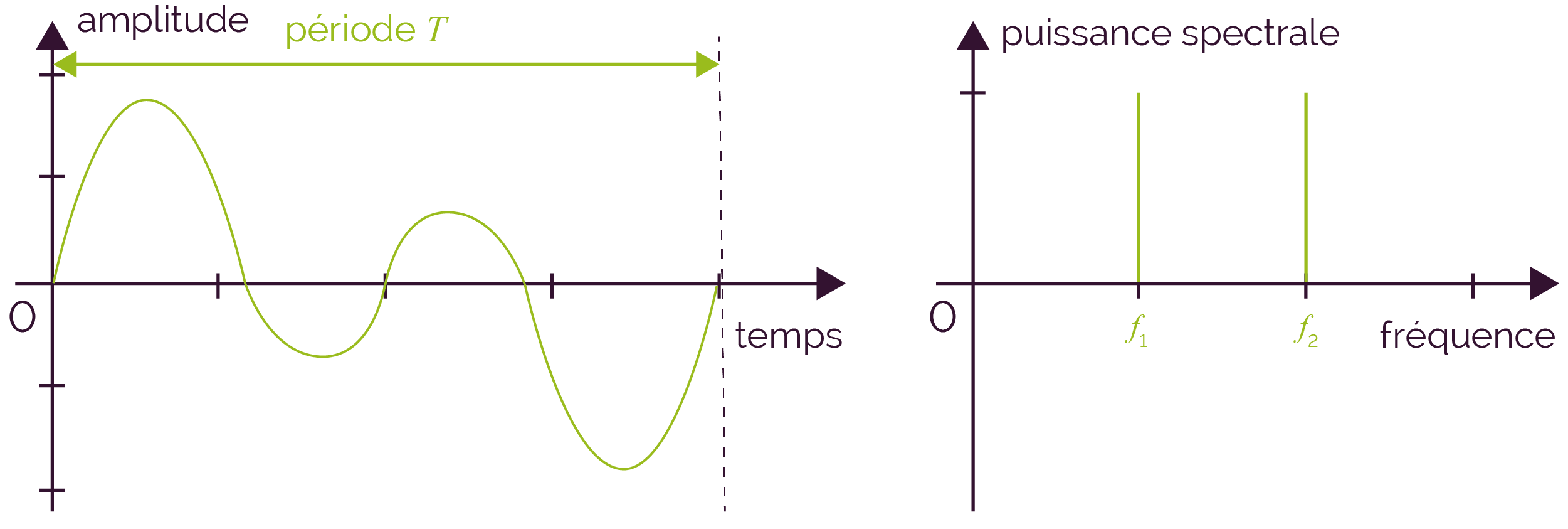
Le théorème de Fourier montre que tout signal périodique de fréquence f₁ et de forme quelconque peut être considéré comme la somme d’un signal sinusoïdal de même fréquence f₁, appelé fondamental, et de signaux de fréquences 2 f₁, 3 f₁, 4 f₁, etc, qui sont appelés harmoniques du signal fondamental.

Exemple
Le visuel ci-dessous montre comment on construit un signal carré : la somme des sinusoïdes de couleurs donne le signal de couleur noire.

Le signal n’est pas tout à fait carré car il n’est construit qu’avec cinq sinusoïdes :

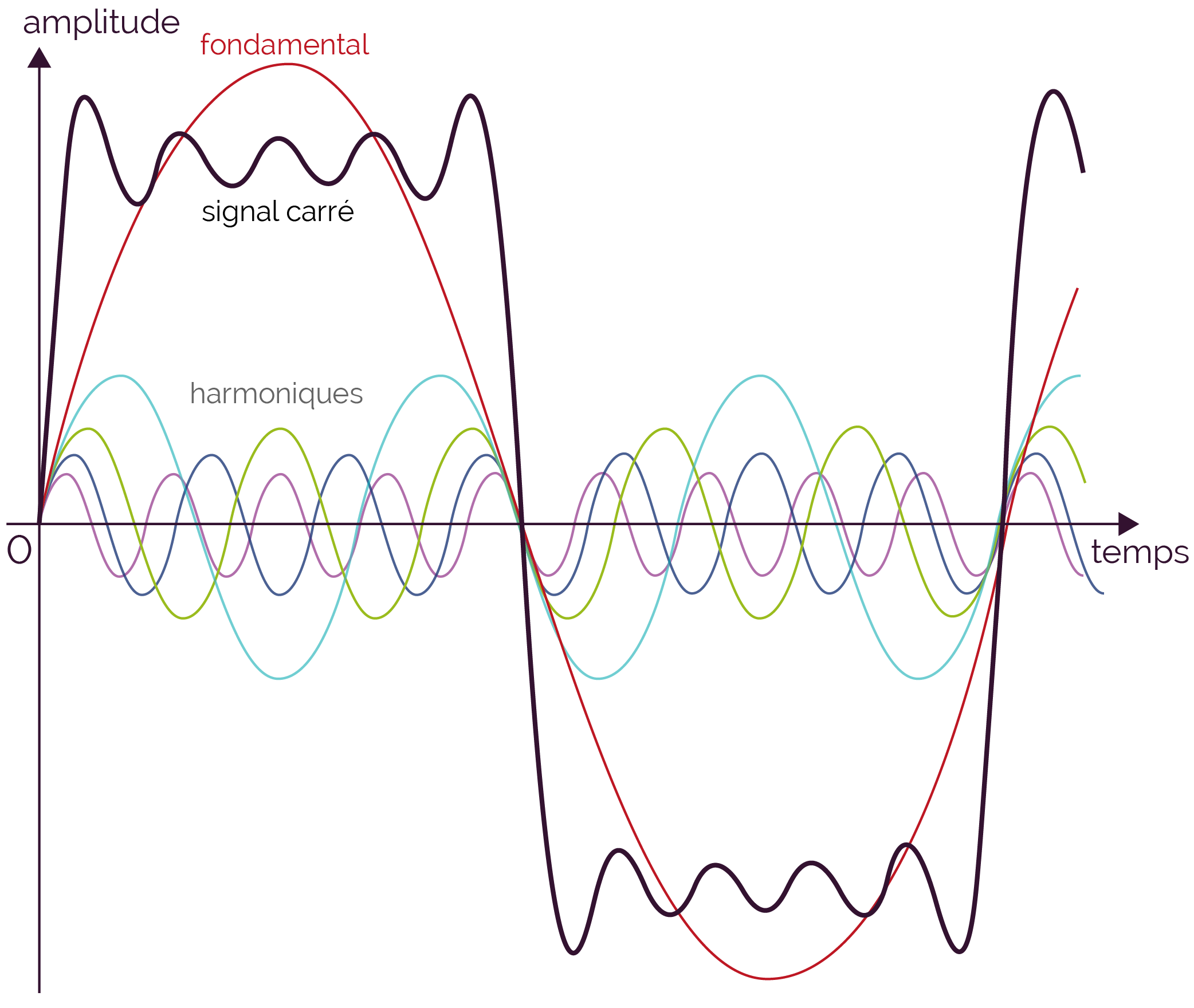
• Le fondamental (courbe rouge) a la même fréquence que le signal carré.
• Les harmoniques ont des fréquences multiples du fondamental.

Selon les fréquences à exclure, les filtres peuvent être de quatre types, qui sont caractérisés par leur gabarit.

Le filtre passe-bas laisse passer les fréquences en dessous de la fréquence de coupure f_c et atténue celles au dessus, d’autant plus qu’elles s’éloignent de f_c.

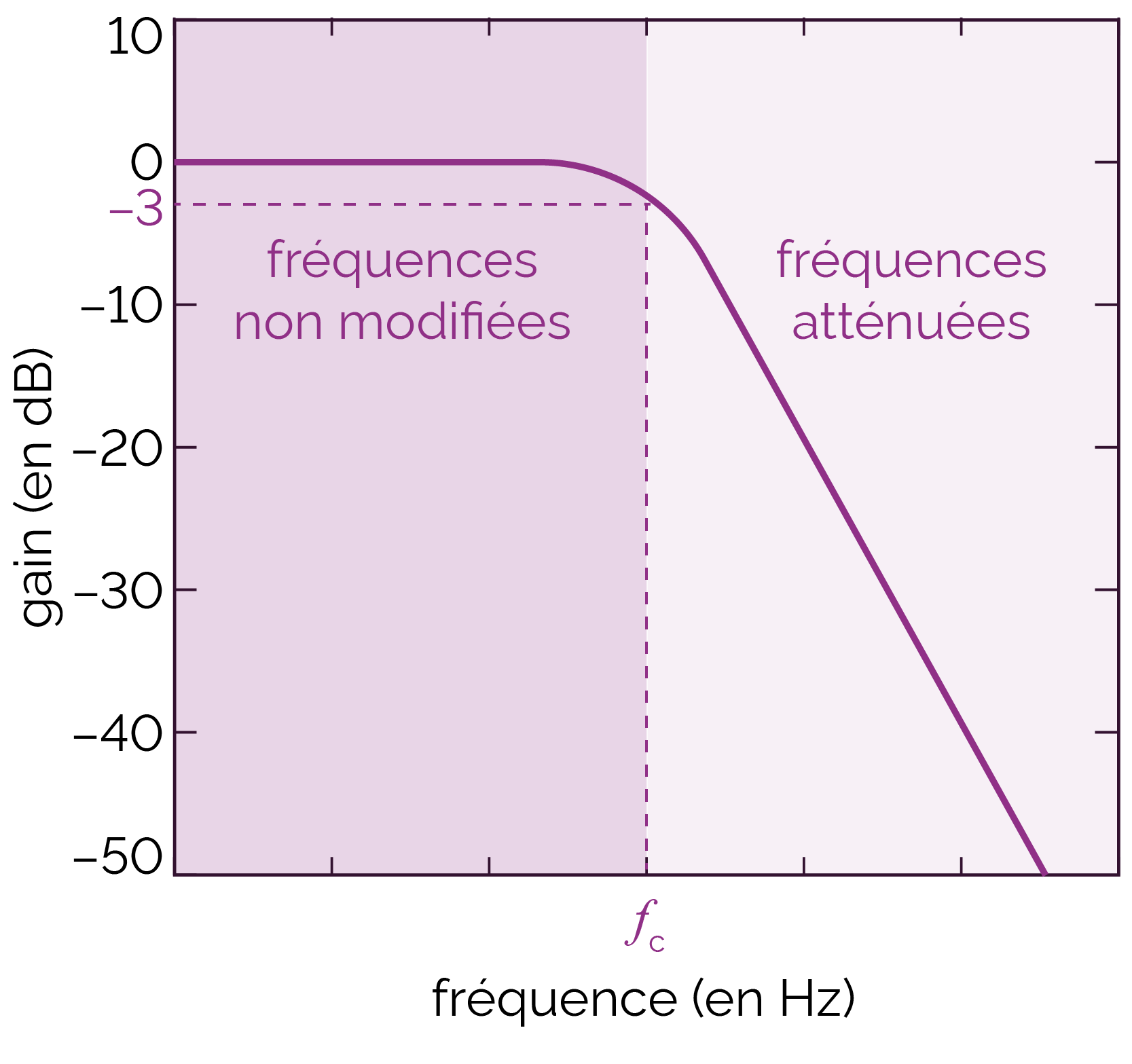
Le filtre passe-haut agit de manière inverse au passe-bas : il laisse passer les fréquences supérieures à f_c mais atténue les fréquences qui lui sont inférieures : il bloque les basses fréquences.

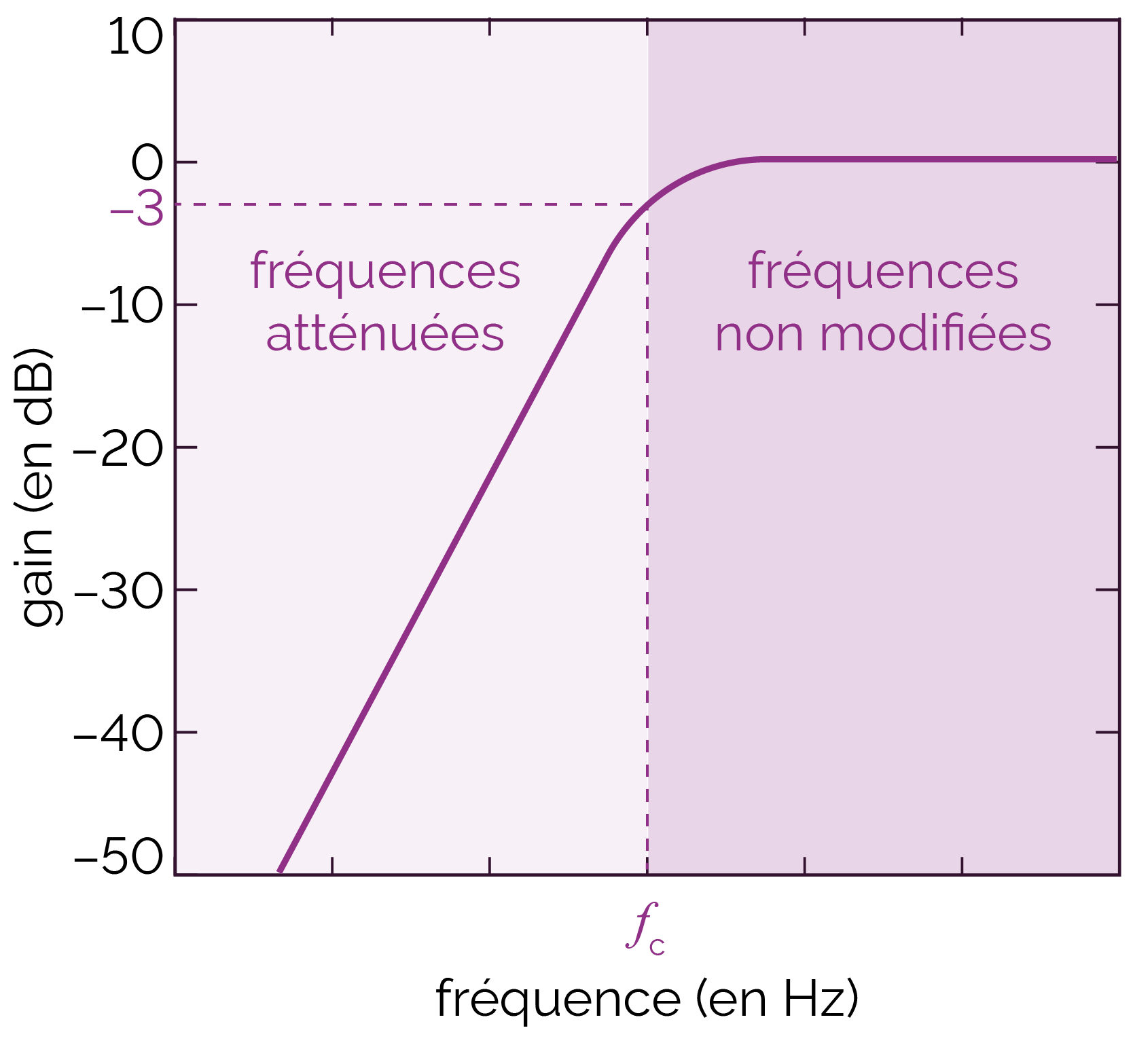
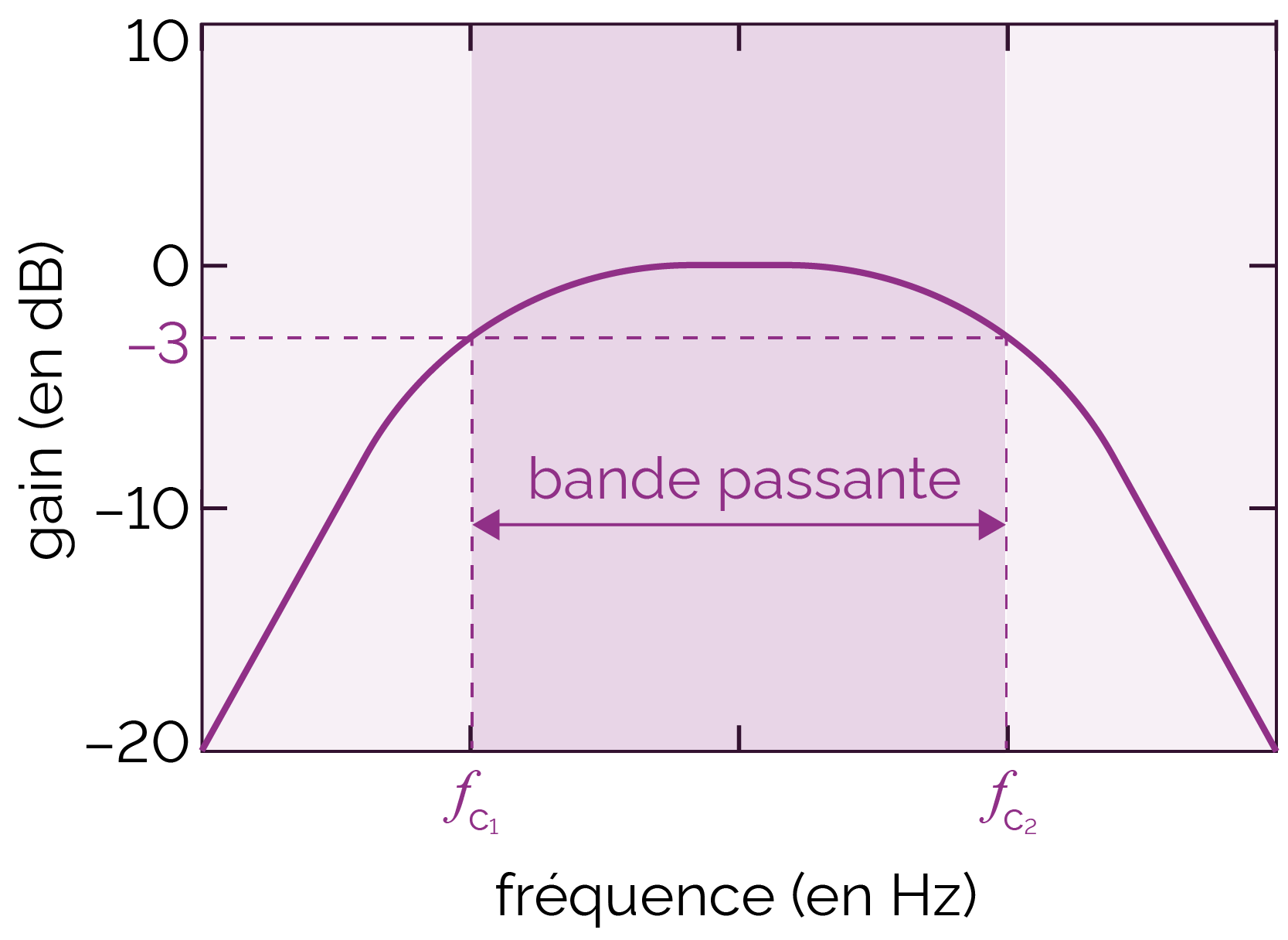
Le filtre passe-bande agit comme un filtre passe-bas et passe-haut simultanément. Ce type de filtre, ainsi que les filtres suivants, font appel à deux fréquences de coupure  et . Le filtre ne laisse passer que la gamme de fréquences située entre ces deux fréquences de coupure, les autres fréquences étant atténuées.

Le filtre coupe-bande fait le contraire d'un filtre passe-bande en bloquant un domaine de fréquences.

Exemple de filtrage d’un signal carré

Signal carré en entrée.
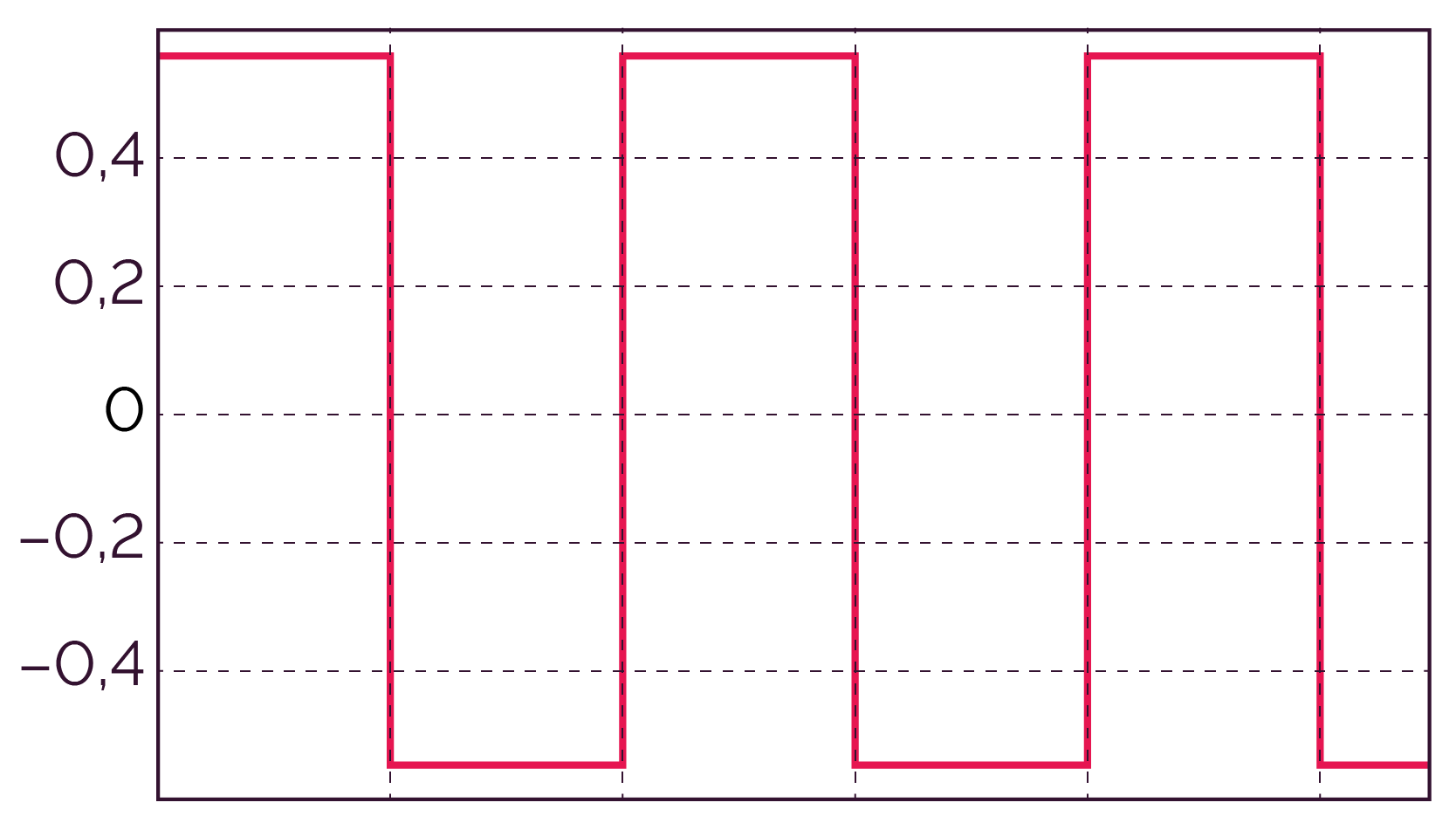
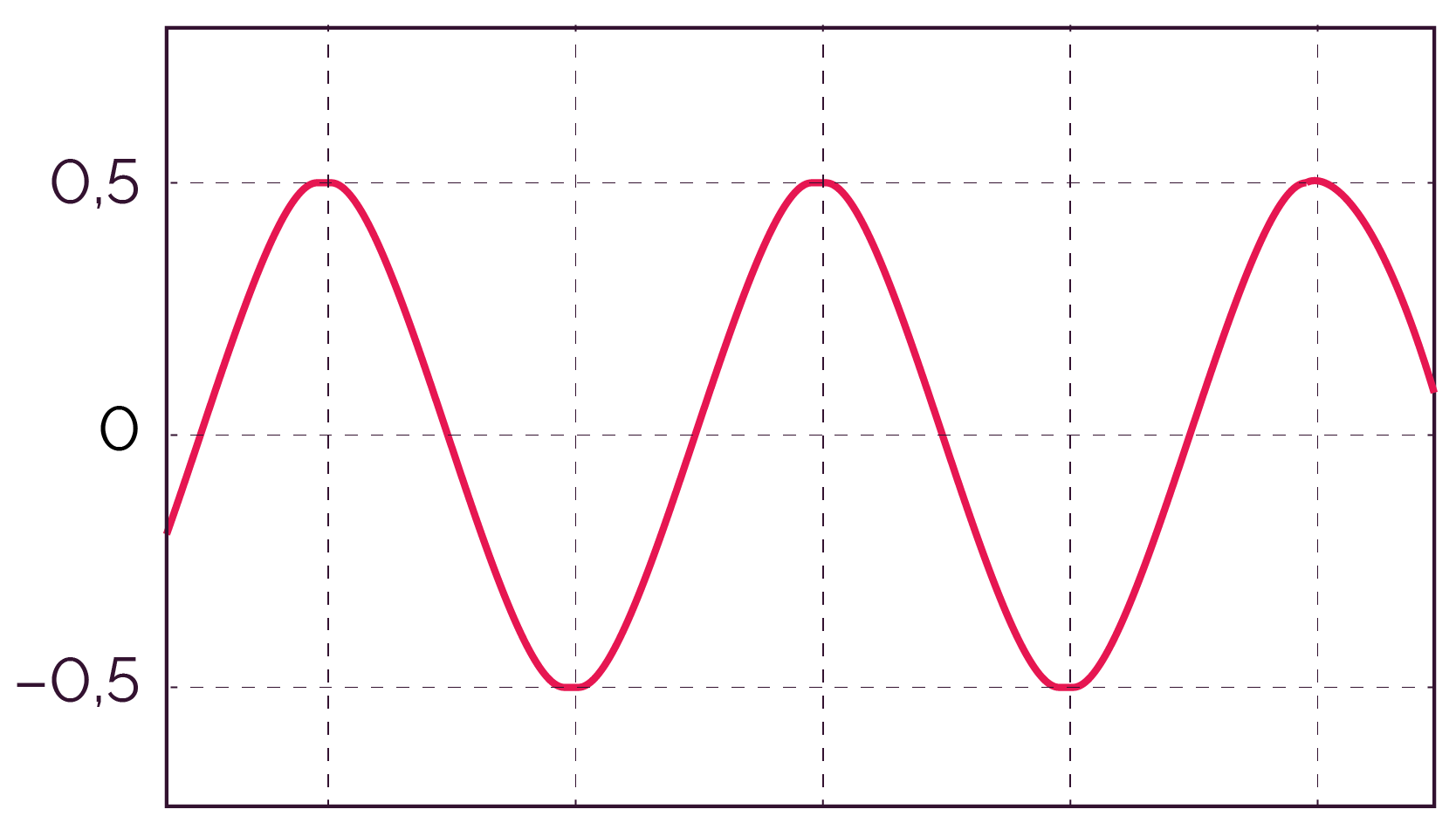
Filtrage passe-bas. Ce filtre ne laisse passer que le fondamental : une sinusoïde de même fréquence que le signal carré.
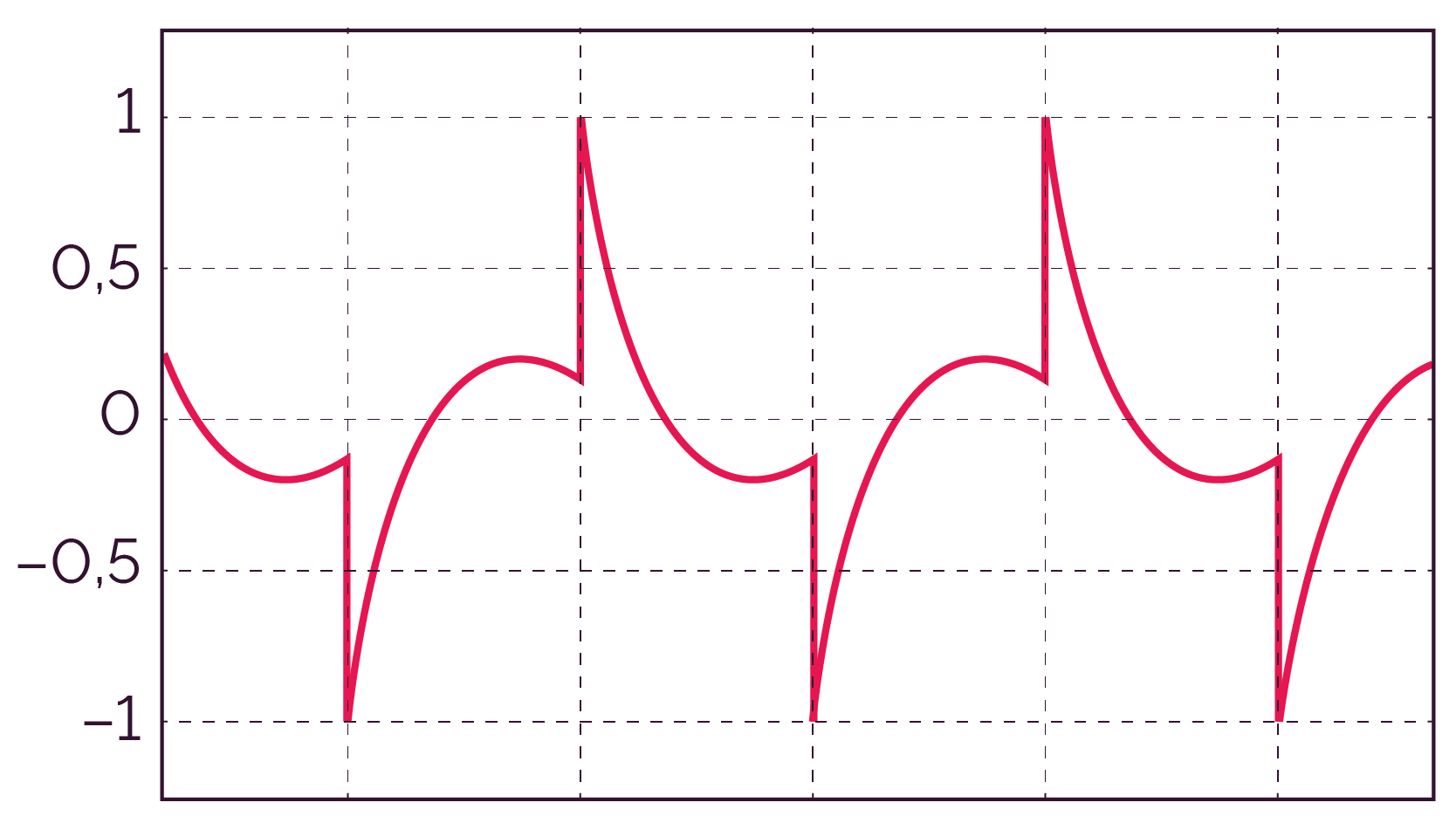
Filtrage passe-haut. Ce filtre ne réagit que lorsque le signal carré varie rapidement, ici sur les fronts, ce qui génère les pics visibles sur le signal.