Fiche de cours

Utilisation de la proportionnalité : les échelles

Collège   >   5eme, 4eme, 3eme   >   Mathématiques   >   Utilisation de la proportionnalité : les échelles

  • Fiche de cours
  • Quiz et exercices
    1
  • Vidéos et podcasts
Objectifs
La recherche ou l’utilisation d’une échelle sur un plan est un cas particulier de la proportionnalité.
Qu’est ce qu’une échelle sur un plan ? Comment utiliser l’échelle d’un plan pour calculer des distances ? Comment calculer l’échelle d’un plan ?
1. Echelles

a. Définition
S’il y a proportionnalité entre les dimensions d’un objet dessiné sur un schéma et ses dimensions réelles, on appelle échelle le rapport de la longueur sur le schéma par la longueur réelle correspondante ; les deux longueurs étant exprimées dans la même unité :

On exprime souvent l’échelle sous la forme d’une fraction avec le numérateur égal à 1 (réduction) ou le dénominateur égal à 1 (agrandissement).

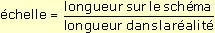
Exemples
• Si une carte est à l'échelle 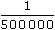, cela signifie que 1 cm sur la carte représente 500 000 cm en réalité :

Les distances sur une carte et sur le terrain sont proportionnelles.
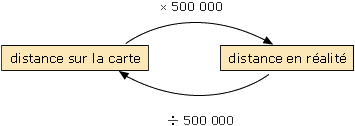
Cette échelle peut aussi s'écrire 1 : 500 000 ou 1 / 500 000.

• Si un croquis est à l'échelle 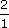, cela signifie que 2 cm sur le dessin correspondent à 1 cm en réalité.
b. Utiliser une échelle
• Calcul d'une longueur réelle 
Sur la carte à l'échelle 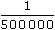, deux villes sont distantes de 9,5 cm.
Quelle distance à vol d'oiseau les sépare en réalité ?
On utilise un tableau de proportionnalité :

x = ( 500 000 × 9,5 )  1 = 4 750 000.
Or  4 750 000 cm = 47,5 km, donc la distance réelle est de 47,5 km.

• Calcul d'une longueur sur une représentation 
Un insecte mesure environ 9 mm de long. On le dessine à l'échelle .
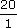Quelle sera la longueur du dessin de cet insecte ?
On peut soit construire un tableau de proportionnalité soit calculer directement.
L'échelle 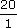signifie que 20 mm sur le dessin correspondent à 1 mm en réalité. Les longueurs sont donc multipliées par 20 sur le dessin, d'où 9 × 20 = 180 mm.
9 mm dans la réalité sont représentés par 180 mm sur le dessin, c'est-à-dire par 18 cm.

• Calculer une échelle
Sur un plan, la largeur d'une cuisine est de 1,7 cm. En réalité, elle est de 3,40 m.
Quelle est l'échelle de ce plan ?

Attention ! les deux dimensions doivent être exprimées avec la même unité : 3,40 m = 340 cm.

On complète le tableau de proportionnalité suivant :

x = ( 340 × 1 )  1,7 = 200 .
1 cm sur le plan représente 200 cm en réalité.
L'échelle de ce plan est   .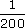

2. Agrandissement et réduction
Si l'échelle est supérieure à 1, il s'agit d'un agrandissement.
Si l'échelle est inférieure à 1, il s'agit d'une réduction.

• Exemple 1
Le négatif d'une photographie est un rectangle de 24 mm sur 36 mm. La photographie est un agrandissement du négatif ; sa longueur est 16,2 cm.
Calculer l'échelle, puis la largeur de la photographie.

16,2 cm = 162 mm.

Conseil : Pour calculer une échelle, mettre le 1 de référence dans le tableau de proportionnalité au niveau des longueurs les plus petites.

 x = ( 162 × 1 )  36 = 4,5 .
4,5 mm sur la photo représentent 1 mm sur le négatif.
L'échelle est 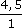 > 1, il s'agit donc bien d'un agrandissement.
La largeur du négatif est égale à 24 mm, donc la largeur de la photographie est 24 × 4,5 = 108 mm = 10,8 cm.

• Exemple 2
Un monument de longueur 110 m est représenté par une maquette de longueur 44 cm.
Calculer l'échelle.

110 m = 11 000 cm.

 x = ( 11 000 × 1 )  44 = 250 .
1 cm sur la maquette représente 250 m en réalité.
L'échelle est x < 1, il s'agit bien d'une réduction.

Évalue ce cours !

 

Note 3.6 / 5. Nombre de vote(s) : 780

Teste dès maintenant tes nouvelles connaissances dans notre quiz

Question 1/5

La médiane de 6 notes est 13. Cela signifie que :
Question 2/5

On a obtenu la série statistique suivante :

Combien vaut la médiane ?
Question 3/5

On a obtenu la série ci-dessous :

Quelle est la médiane de cette série ?
Question 4/5

On a relevé les tailles en cm des élèves d’une classe :

 

Parmi les propositions suivantes, laquelle est vraie ?
Question 5/5

Les notes en français de deux classes littéraires sont données dans le tableau suivant :

Quelle est la note médiane ?

Vous avez obtenu75%de bonnes réponses !

Reçois l’intégralité des bonnes réponses ainsi que les rappels de cours associés

Une erreur s'est produite, veuillez ré-essayer

Consultez votre boite email, vous y trouverez vos résultats de quiz!

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

 

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

 

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT

Fiches de cours les plus recherchées

Mathématiques

Utilisation de la proportionnalité : durée et vitesse

Mathématiques

Utilisation de la proportionnalité : pourcentages

Mathématiques

Calculs enchaînés sur les nombres

Mathématiques

Comparaison des nombres relatifs

Mathématiques

Equations-produits

Mathématiques

Équations du premier degré à une inconnue

Mathématiques

Mise en équation ou en système d'équations d'un problème

Mathématiques

Fractions irréductibles

Mathématiques

Fonctions linéaires

Mathématiques

Notions de fonctions