Fiche de cours

Tracer une droite du plan- Seconde- Mathématiques

Lycée > Seconde > Mathématiques > Tracer une droite du plan- Seconde- Mathématiques

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectifs

Tracer une droite du plan connaissant son équation réduite.
Tracer une droite du plan connaissant son équation cartésienne.

Points clés

Toutes les droites du plan sont caractérisées par leur équation, qui peut s’écrire de deux façons différentes : on parle d’équation réduite ou d’équation cartésienne d’une droite.
Il existe différentes méthodes pour tracer une droite connaissant son équation, qu’elle soit réduite ou cartésienne.
Pour tracer une droite dont on connait l’équation réduite, on peut utiliser une méthode à partir de deux points de la droite.
Pour tracer une droite dont on connait l’équation réduite, on peut utiliser une méthode à partir de la valeur de l’ordonnée à l’origine et du coefficient directeur.
Pour tracer une droite dont on connait une équation cartésienne, on peut utiliser une méthode à partir de deux points de la droite.
Pour tracer une droite dont on connait une équation cartésienne, on peut utiliser une méthode à partir de la valeur de l’ordonnée à l’origine et d’un vecteur directeur.

Pour bien comprendre

Connaitre l’équation réduite d’une droite, de la forme y = ax + b, où a est la pente (ou coefficient directeur) et b est l’ordonnée à l’origine.
Savoir que le coefficient directeur a de la droite qui passe par les points A(x_A ; y_A) et B(x_B ; y_B) est donné par la formule 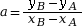. Il représente le déplacement qu’il faut faire, en suivant les axes du repère, pour passer du point A au point B.
Connaitre l’équation cartésienne d’une droite.
Trouver un vecteur directeur d’une droite dont on connait une équation cartésienne.

Dans tout ce cours, le plan est muni d’un repère orthonormé .

1. Équation réduite et équation cartésienne d'une droite

Toutes les droites du plan sont caractérisées par leur équation, qui peut s’écrire de deux façons différentes : on parle d’équation réduite ou d’équation cartésienne d’une droite.

Une équation réduite est de la forme :

y = mx + p, où m et p sont des nombres réels (m ≠ 0), si elle n’est pas parallèle à l’axe des ordonnées ;
x = c, où c est un nombre réel, si elle est parallèle à l’axe des ordonnées ;
y = p, où p est un nombre réel, si elle est parallèle à l’axe des abscisses.

Une équation cartésienne est de la forme ax + by + c = 0 (a, b et c ∈ ℝ et au moins l’un des nombres a et b non nul).

On peut facilement passer d’une écriture sous la forme d’une équation réduite à une écriture sous la forme d’une équation cartésienne, et inversement.

Il existe différentes méthodes pour tracer une droite connaissant son équation, qu’elle soit réduite ou cartésienne.

2. Tracer une droite connaissant son équation réduite y = mx + p

a. En calculant les coordonnées de deux points

Méthode en calculant les coordonnées de deux points

Pour tracer une droite à partir de son équation réduite, on peut :

choisir de manière arbitraire deux valeurs de x et calculer, à l’aide de l’équation réduite, les valeurs correspondantes de y ;
placer alors les deux points obtenus dans le repère ;
relier les deux points pour obtenir la droite souhaitée.

Remarque
À la première étape de la méthode, il est souvent plus facile de choisir 0 et 1 comme valeurs de x. Ces valeurs simplifient les calculs.

Exemple
Dans le repère

, tracer la droite (d₁) d’équation y = 2x + 1.

On choisit arbitrairement deux valeurs de x, par exemple 0 et 1. On calcule les valeurs de y correspondantes.
Pour x = 0, on a : y = 2 × 0 + 1 = 1. (d₁) passe donc par le point A(0 ; 1).
Pour x = 1, on a : y = 2 × 1 + 1 = 3. (d₁) passe donc par le point B(1 ; 3).
On place ces deux points dans le repère.
On trace la droite qui relie les deux points. On obtient la représentation graphique de (d₁) :

Remarque
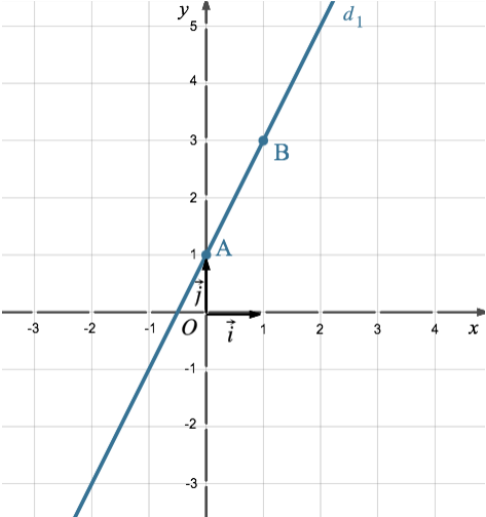
Parfois, la recherche des coordonnées de deux points de la droite se présente sous la forme d’un tableau. Pour l’exemple précédent, on aurait pu présenter la démarche sous la forme suivante :

x	0	1
y	2 × 0 + 1 = 1	2 × 1 + 1 = 3

Avec cette présentation, les coordonnées des deux points se lisent dans les colonnes du tableau. Le premier point a pour coordonnées (0 ; 1) et le deuxième (1 ; 3).

b. En calculant la valeur de l'ordonnée à l'origine et en utilisant le coefficient directeur

Méthode à partir de l’ordonnée à l’origine et du coefficient directeur

Pour tracer une droite à partir de son équation réduite, on peut :

calculer la valeur de l’ordonnée à l’origine, c’est-à-dire la valeur de y pour laquelle x = 0. Soit A ce premier point de coordonnées (0 ; y(0)) ;
placer le point A dans le repère ;
à l’aide du déplacement que représente le coefficient directeur, placer un second point de la droite à partir du point A ;
relier les deux points pour obtenir la droite souhaitée.

Exemple 1
Dans le repère

, tracer la droite (d₂) d’équation

On calcule la valeur de l’ordonnée à l’origine, c’est-à-dire la valeur de y pour laquelle x = 0.
On a :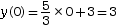 donc (d₂) passe par le point A de coordonnées (0 ; 3).
On place le point A(0 ; 3) dans le repère.
Dans l’équation 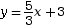, on lit que le coefficient directeur de la droite vaut 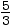. Donc en partant de A, il faut faire un déplacement de + 3 horizontalement et de + 5 verticalement. On place ainsi un second point dans le repère.
On trace la droite qui relie les deux points. On obtient la représentation graphique de (d₂) :

Remarque
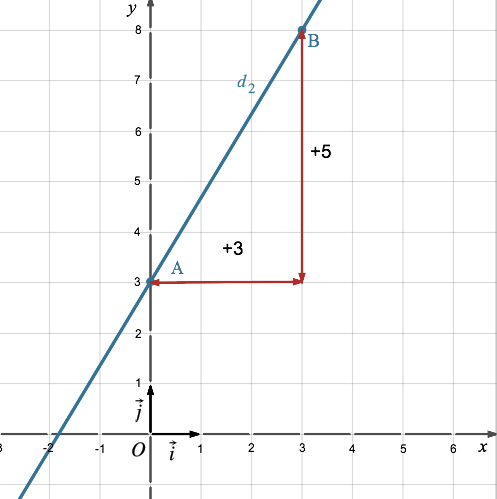
Une pente a donnée en écriture décimale correspond à un déplacement de 1 horizontalement pour a verticalement.

Exemple 2
Dans le repère

, construire la droite (d₃) d’équation y = −2x + 4.

On calcule la valeur de l’ordonnée à l’origine, c’est-à-dire la valeur de y pour laquelle x = 0.
On a : y(0) = −2 × 0 + 4 = 4 donc (d₂) passe par le point A de coordonnées (0 ; 4).
On place le point A(0 ; 4) dans le repère.
Dans l’équation y = −2x + 4, on lit que le coefficient directeur de la droite vaut −2 qui peut s’écrire 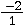. En partant de A, il faudra donc faire un déplacement de + 1 horizontalement et de − 2 verticalement. On place ainsi un second point dans le repère.
On trace la droite qui relie les deux points. On obtient la représentation graphique de (d₃) :

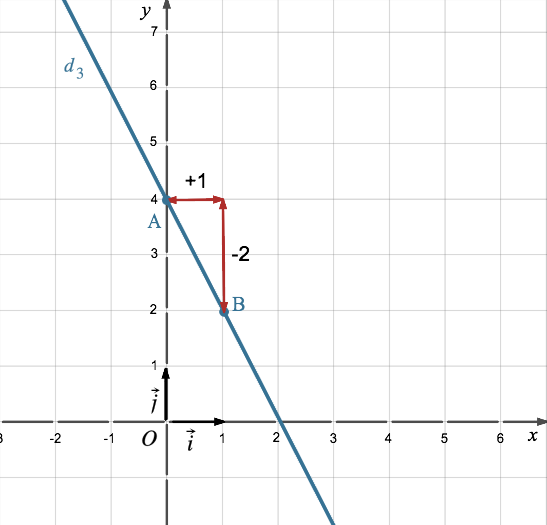
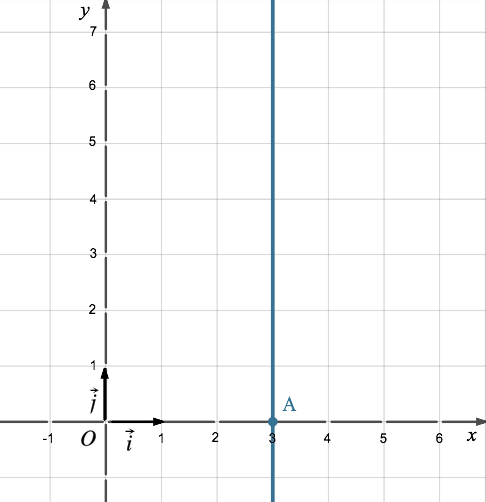
c. Cas particulier des droites d'équation x = c

Rappel
Une droite d’équation x = c (c

) est parallèle à l’axe des ordonnées et passe par le point A(c ; 0).

Exemples

Voici la représentation graphique de la droite d'équation x = 3 :
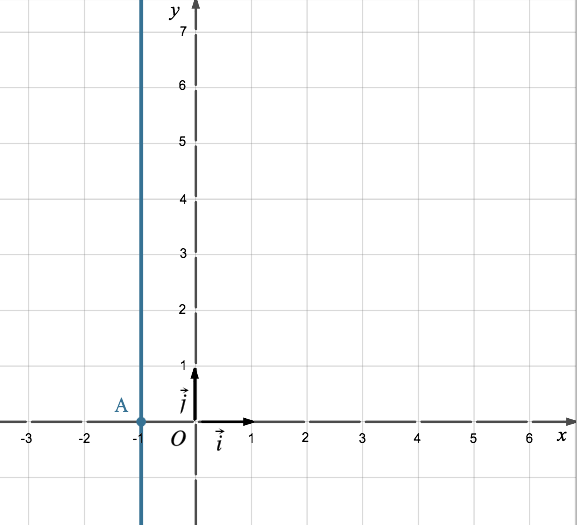
Et celle de la droite d'équation x = –1 :

3. Tracer une droite connaissant son équation cartésienne ax + by + c = 0

a. En calculant les coordonnées de deux points

Méthode en calculant les coordonnées de deux points

Pour tracer une droite à partir de son équation cartésienne, on peut :

choisir de manière arbitraire deux valeurs de x et calculer, à l’aide de l’équation cartésienne, les valeurs correspondantes de y ;
placer alors les deux points obtenus dans le repère ;
relier les deux points pour obtenir la droite souhaitée.

Exemple
Dans le repère

, tracer la droite (d₄) d’équation −3x + 2y − 6 = 0.

On choisit arbitrairement deux valeurs de x, par exemple 0 et 2. On calcule les valeurs de y correspondantes.
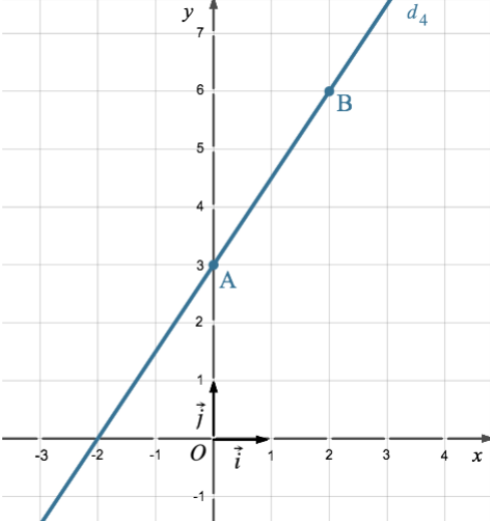
Pour x = 0, on a : −3 × 0 + 2y − 6 = 0 soit 2y − 6 = 0 d’où y = 3. (d₄) passe donc par le point A(0 ; 3).
Pour x = 2, on a : −3 × 2 + 2y − 6 = 0 soit −6 + 2y −6 = 0 d’où y = 6. (d₄) passe donc par le point B(2 ; 6).
On place ces deux points A(0 ; 3) et B(2 ; 6) dans le repère.
On trace la droite qui relie les deux points. On obtient la représentation graphique de (d₄) :

b. En calculant la valeur de l'ordonnée à l'origine et en utilisant un vecteur directeur

Méthode à partir de l’ordonnée à l’origine et d’un vecteur directeur

Pour tracer une droite à partir de son équation cartésienne, on peut :

calculer la valeur de l’ordonnée à l’origine, c’est-à-dire la valeur de y pour laquelle x = 0. Soit A ce premier point de coordonnées (0 ; y(0)) ;
placer le point A dans le repère ;
identifier les coordonnées d’un vecteur directeur 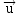de la droite.
D’après un théorème du cours, si ax + by + c = 0 est une équation cartésienne d’une droite (d), alors le vecteur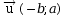 est un vecteur directeur de (d) ;
à l’aide du vecteur directeur 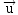, placer un second point de la droite à partir du point A ;
relier les deux points pour obtenir la droite souhaitée.

Exemple
Dans le repère

, tracer la droite (d₅) d’équation −x + 3y − 6 = 0.

On calcule la valeur de l’ordonnée à l’origine, c’est-à-dire la valeur de y pour laquelle x = 0.
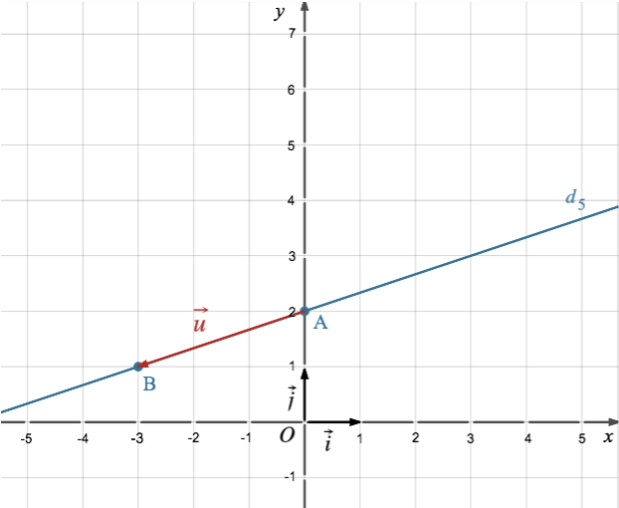
On a : y(0) = −0 + 3y − 6 = 0 soit 3y − 6 = 0 d’où y = 2. (d₅) passe par le point A de coordonnées (0 ; 2).
On place le point A(0 ; 2) dans le repère.
On identifie les coordonnées d’un vecteur directeur 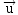de (d₅) à partir des coefficients de l’équation −x + 3y − 6 = 0 : .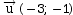
On place B, un second point de la droite, dans le repère, à l’aide de la relation .
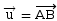On trace la droite qui relie les deux points. On obtient la représentation graphique de (d₅) :

Évalue ce cours !

Note 3.6 / 5. Nombre de vote(s) : 21

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT