Les structures répétitives ou itératives (boucles)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
• Utiliser, créer un algorithme.
• Traduire un algorithme sur une machine (calculatrice ou autre).
Par habitude, on utilise :
• I, J, K entiers utilisés comme compteurs (boucles).
• N, M entiers d’utilisations diverses (suites…).
• X, Y, Z réels pour des coordonnées (géométrie) ou en auxiliaires de calcul.
Pour cette fiche, on considérera principalement trois structures.
Remarque
Cette boucle s’utilise chaque fois que l’on connaît le nombre d’itérations à effectuer.
Exemple
Somme des n + 1 premiers entiers (de 0 à n cela en fait n + 1).
Le principe
On demande l’entier jusqu’où la somme doit être effectuée, puis par une boucle itérative réalisée n fois, on additionne les entiers successifs les uns après les autres. Afficher le résultat.
Algorithme
| SOMENT (Version 1) |
|
Variables I, N entiers, S nombre Entrées Lire N Traitement Afficher « Somme des entiers jusqu’à N » Afficher « Entrer un nombre entier » Entrer N Affecter S de 0 POUR I variant de 0 jusqu’à N Affecter S de S+I FINPOUR Sorties Afficher « Somme de 0 jusqu’à », N Afficher S |
Traduction sur calculatrice
|
TI- 84 TI-82 Stat TI-82 |
|
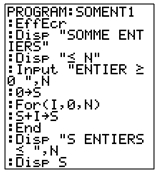
Utilisation
|
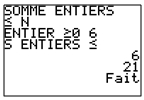
| Casio Graph 35+ |
|
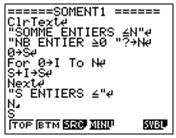
Utilisation
|
| TI-Nspire CAS |
|
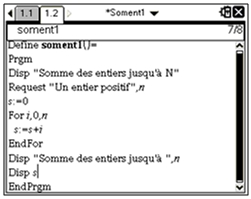
Utilisation
|
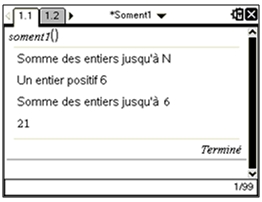
Remarque
Parfois dans la boucle Pour… on utilise un « pas » différent de 1, c'est-à-dire que la variable augmente, par exemple de 2 en 2 ou de 0,1 en 0,1 ou autres...
Par exemple, les valeurs successives d’une fonction peuvent se faire de 0,5 en 0,5.
Le principe
Cette boucle conditionnelle est très utile. Il est demandé de réaliser un traitement, Tant Que une certaine condition est vraie.
Exemple
S’il faut ranger des livres, on dira : « tant qu’il reste des livres, ranger ». C’est une boucle qui sera très souvent utilisée.
Raisonnement
Nous avons vu (Fiche d’introduction) un petit programme permettant de dire si un entier est pair ou impair. La méthode utilisée demandait de connaître la partie entière d’un nombre et de faire la recherche de la moitié du nombre donné. Alors que si la question nous était posée, nous ne regarderions que le dernier chiffre du nombre pour répondre.
Une idée… si un nombre est plus petit que dix (strictement), nous pouvons immédiatement le comparer à 0, 2…
Et si ce nombre est plus grand que dix (sens large), en lui enlevant dix Tant Qu’il a plus qu’un seul chiffre, on finira forcement par obtenir un nombre entre 0 et 9.
Cette idée permet de réaliser l’algorithme suivant.
Algorithme
| Pair Impair (Version 3) |
|
Variables N, M entiers Entrées Lire N Traitement Afficher « Pair-Impair Version 3 » Afficher « Entrer un nombre entier » Entrer N Affecter M de N TantQue 10<M Affecter M de M-10 FinTantQue Si M=0 ou M=2 ou M=4 ou M=6 ou M=8 Alors Afficher N, ‘ Pair’ Sinon Afficher N, « Impair » FinSi Sorties Affichages du traitement |
Traduction sur calculatrice
|
TI- 84 TI-82 Stat TI-82 |
|
Utilisation
|
| Casio Graph 35+ |
|
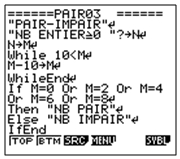
Utilisation |
| TI-Nspire CAS |
|
Utilisation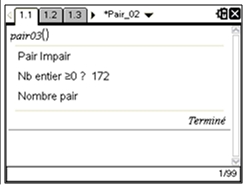
|
Remarques
• La condition est analysée à l’entré de la boucle, si la condition n’est pas réalisée, la boucle ne sera jamais parcourue.
• La boucle est parcourue tant que la condition est vraie.
• On ne connaît pas à l’avance le nombre de fois où cette boucle sera réalisée.
Le principe
Cette boucle conditionnelle ressemble un peu à la précédente. Son principe est identique. Répéter un traitement jusqu’à ce que une certaine condition devienne vraie.
Exemple
Dans l’exemple signalé précédemment pour le rangement de livres, cette instruction deviendrait :
« Ranger les livres Jusqu’à ce qu’il n’y en ait plus à ranger ».
Il vous est conseillé de bien chercher et comprendre ce qui différencie ces deux boucles.
Un exemple d’application a déjà été vu. Vouloir vérifier que le nombre entré au clavier de la machine est bien un nombre entier positif correspond exactement à ce type de boucle.
Remarques
La boucle à utiliser est la boucle « répéter… jusqu’à ce que ».
Sur la Graph35+ cette instruction n’existe pas, on utilise alors, avec un changement dans la condition, la boucle « tant que ».
De même sur la TI-Nspire CAS, cette boucle existe en LUA à partir du logiciel ordinateur. Sur la calculatrice on utilisera aussi la boucle « tant que ».
Algorithme (uniquement la partie à rajouter au précédent)
| Pair Impair (Version 3bis) | Commentaires éventuels |
|
Répéter Afficher « Entrer un nombre entier positif » Entrer N Jusqu’à ce que PartieEntière (N)=N ET 0  N |
Version Répéter JusquàCeQue |
Traduction sur calculatrice
|
TI- 84 TI-82 Stat TI-82 |
|
Quand cette instruction n’existe pas, on utilise la boucle TantQue. Elle demande de changer la condition et de faire en sorte que cette condition soit réalisée AVANT d’entrer dans la boucle.
Exemple pour les deux calculatrices indiquées
| Pair Impair (Version 3ter) | Commentaires éventuels |
|
Affecter N par -1 TantQue PartieEntière (N)≠N OU N<0 Afficher « Entrer un nombre entier positif » Entrer N FinTantQue |
Version TantQue Il est nécessaire d’initialiser la variable sur qui porte la condition. |
Traduction sur calculatrice
| Casio Graph 35+ | TI-Nspire CAS |
|
|
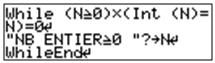
Remarques
• La condition est analysée à la fin de la boucle, si la condition n’est pas réalisée, la boucle sera tout de même parcourue une fois.
• La boucle est parcourue jusqu'à ce que la condition devienne vraie (elle est donc parcourue Tant Que la condition est fausse).
• On ne connaît pas à l’avance le nombre de fois où cette boucle sera réalisée.
Exemple
Calculer la somme des n + 1 premiers entiers (de 0 à n).
Un algorithme à déjà été utilisé, traduit en programmes pour les calculatrices indiquées. C’est un algorithme itératif ou impératif (les instructions à effectuer sont écrites les une après les autres et à effectuer comme tel).
LE PRINCIPE RECURSIF
Si n = 0 alors la somme c’est 0. Sinon, la somme c’est n + la somme des (n-1) premiers entiers.
Faisons tourner (à la main) cela pour la somme des entiers jusqu’à 2 :
• Étape 1 : Somme des entiers jusqu’à n = 2.
Est-ce que n = 0 ? non. Il faut donc calculer 2 + Somme des entiers jusqu’à 2-1 = 1.
• Étape 2 : Somme des entiers jusqu’à n = 1.
Est-ce que n = 0 ? non. Il faut donc calculer 1 + Somme des entiers jusqu’à 1-1 = 0.
• Étape 3 : Somme des entiers jusqu’à n = 0.
Est-ce que n = 0 ? Oui. Donc (à ce stade) S=0, il n’y a plus d’appel récursif, c’est terminé (ou presque).
Il faut alors additionner les résultats de chaque étape (c’est automatique).
0 (étape 3) + 1 (étape 2) + 2 (étape 1) = 3. Ce qui est le bon résultat.
Le programme a réalisé des calculs grâce à une boucle qui (apparemment) ne nous a pas demandé de gérer les différentes étapes.
Voici un algorithme récursif de ce programme (seule la fonction est récursive, le programme n’est là que pour la présentation).
| SOMENT (Version récursive) | Commentaires éventuels |
|
Variables I, N entiers, S nombre Entrées Lire N Traitement Afficher « Somme des entiers jusqu’à N » Affecter N par -1 TantQue PartieEntière (N)≠N OU N<0 Afficher « Entrer un nombre entier positif » Entrer N FinTantQue Affecter S de Somentrecf(n) Sorties Afficher « Somme de 0 jusqu’à », N Afficher S |
Ceci n’est que pour la présentation et
pour introduire le nombre dans la machine. Appel de la fonction récursive. |
| Somentrecf(n) (La fonction récursive) | Commentaires éventuels |
|
Variables N entier Entrées N Traitement Si n=0 alors Retourner 0 Sinon Retourner n + Somentrecf(n-1) FinSi Sorties S |
Si n vaut 0 alors S vaut 0, valeur qu’il faut
faire remonter (Return). Sinon, la somme c’est n + (la somme des entiers jusqu’à n-1). |
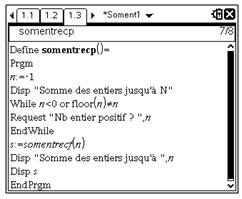
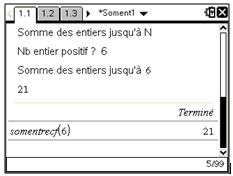
Traduction sur calculatrice TI-Nspire Cas (programmation récursive)
| TI-Nspire CAS |
 
|
On remarquera qu’il est possible de n’appeler QUE la fonction récursive pour obtenir le résultat demandé (sans vérifier la validité du nombre entré).
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Mathématiques
Puissance n-ième d'une matrice carrée d'ordre 2 ou 3
Mathématiques
Écriture matricielle d'un système d'équations linéaires
Mathématiques
Suites de matrices colonnes
Mathématiques
Étude asymptotique d'une marche aléatoire
Mathématiques
Positions relatives de droites et de plans
Mathématiques
Orthogonalité de deux droites, d'une droite et d'un plan
Mathématiques
Caractérisation d'un plan
Mathématiques
Nombres premiers : questionnements et nombres premiers particuliers (application RSA)
Mathématiques
Représentation paramétrique d'une droite et d'un plan
Mathématiques
Comparaison de suites
Fermer
Accédez gratuitement à
