Représentation paramétrique d'une droite et d'un plan
- Fiche de cours
-
Quiz et exercices
1
- Vidéos et podcasts
un
repère de l'espace.
(u ; v ; w).
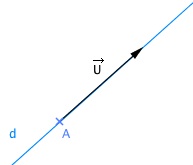
.Les coordonnées de M vérifient donc le système suivant :
(S) =
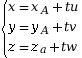avec t ∈ 
.
Le nombre t est appelé le paramètre de cette représentation.
pour obtenir une nouvelle représentation
paramétrique de la droite (d).(-1 ; 2
; 1) est 
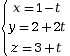avec t ∈ .
et 
non colinéaires et
d'un point A permet de définir entièrement
un plan. On l'appelle le plan passant par A et de
vecteurs directeurs et.Un point M (x ; y ; z) appartient au plan P passant par A (xA ; yA ; zA) et de vecteurs directeurs
(u1 ; u2 ; u3)
et (v1 ; v2 ; v3)
signifie qu'il existe des nombres réels t
et t' tels que 
.Les coordonnées de M vérifient dont le système suivant :
(S) =
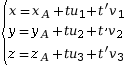avec t et t'
∈ .
Les nombres t et t' sont appelés les paramètres de cette représentation.
pour obtenir une autre
représentation paramétrique.
(1 ; 0 ;
1) et(1 ;
2 ; 5) est 
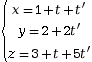avec t et t'
∈ .
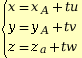.• La représentation paramétrique d'un plan est
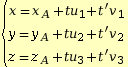.• Il existe une infinité de représentations paramétriques pour une même droite ou un même plan.
Évalue ce cours !
Teste dès maintenant tes nouvelles connaissances dans notre quiz
Vous avez obtenu75%de bonnes réponses !
Reçois l’intégralité des bonnes réponses ainsi que les rappels de cours associés
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Mathématiques
Les différents raisonnements mathématiques- Première- Mathématiques
Mathématiques
Construire un arbre de probabilité- Première- Mathématiques
Mathématiques
Le vocabulaire de la logique- Première- Mathématiques
Mathématiques
Bases et repères de l'espace
Mathématiques
Coordonnées dans une base et applications
Mathématiques
Les suites numériques : comparaison, théorème des gendarmes
Mathématiques
Les limites de fonctions usuelles
Mathématiques
La primitive comme solution d'une équation différentielle y'=f
Mathématiques
L'intégration par parties
Mathématiques
Droites de l'espace : vecteurs directeurs d'une droite, vecteurs colinéaires
Fermer
Accédez gratuitement à
