Terminale > Mathématiques > Fonction convexe et fonction concave sur un intervalle

Fonction convexe et fonction concave sur un intervalle

Fiche de cours Vidéos Quiz Profs en ligne Télécharger
le pdf

Objectif(s)

• Reconnaître graphiquement les fonctions convexes et concaves.
• Utiliser le lien entre convexité et sens de variation de la dérivée.
• Reconnaître graphiquement un point d’inflexion.
• Croissance comparée et positions relatives des courbes représentatives des fonctions :

Rappel : on considère que toute fonction (définie) dérivable sur un intervalle est continue sur cet intervalle.

1. Définitions : fonction convexe, fonction concave

• Une fonction f, définie, dérivable (donc continue) sur un intervalle I est convexe sur I si sa représentation graphique est entièrement située au-dessus de chacune de ses tangentes.

• Une fonction f, définie, dérivable (donc continue) sur un intervalle I est concave sur I si sa représentation graphique est entièrement située en-dessous de chacune de ses tangentes.

Exemples

• La fonction carrée

est une fonction convexe sur

• La fonction racine carrée

est une fonction concave sur

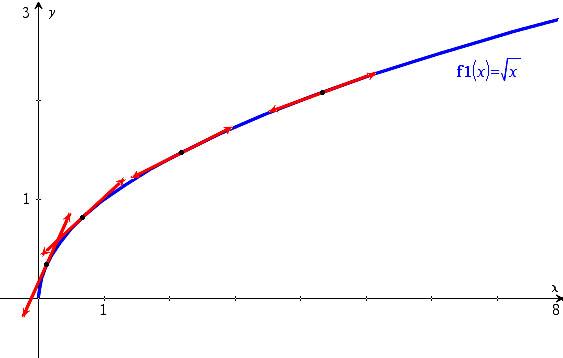
• La fonction cube

est concave sur

et convexe sur

2. Reconnaître une fonction convexe et une fonction concave

Pour une fonction f définie dérivable sur un intervalle I, f ’ sa fonction dérivée.

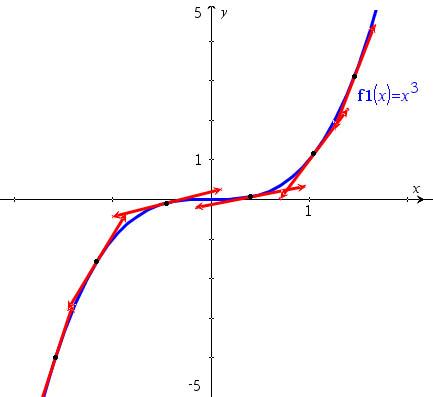
• f est convexe sur I si et seulement si sa dérivée f ’ est croissante sur I.
• f est concave sur I si et seulement si sa dérivée f ’ est décroissante sur I.

Remarque : une fonction est croissante lorsque sa dérivée est positive. Il apparaît donc logique de s’intéresser au signe de la dérivée de f ’(x).

3. Propriétés

a. Définition de la dérivée seconde d'une fonction

Soit f dérivable sur I, dont la fonction dérivée f ’ sur cet intervalle est dérivable, on appelle fonction dérivée seconde de f sur I la dérivée de f ’.

Notation :

Exemple : soit

définie sur

. Sa dérivée est

définie sur

, alors sa dérivée seconde, définie sur

, s’écrit :

b. Propriétés des fonctions convexe et concave

• Si f ’’(x)

0 sur I, alors f est convexe sur I.

On remarquera que dans ce cas puisque la dérivée de la dérivée est positive cela veut dire que la dérivée est croissante, donc le coefficient directeur des tangentes augmente de plus en plus, la croissance de la fonction est donc de plus en plus forte.

• Si f ’’(x)

0 sur I, alors f est concave sur I.

On remarquera que dans ce cas puisque la dérivée de la dérivée est négative cela veut dire que la dérivée est décroissante, donc le coefficient directeur des tangentes devient de plus en plus faible, la croissance de la fonction est donc de moins en moins forte.

Exemple : Soit

définie sur

. Sa dérivée première est

et sa dérivée seconde :

avec

pour x = 1.

D’où le tableau de variations, de signe de la dérivée seconde et de convexité de la fonction :

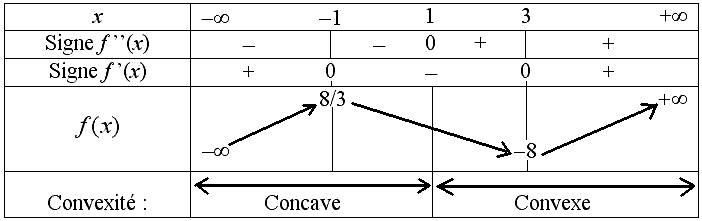
On remarquera que la convexité change pour x = 1. Au point

, la courbe traverse sa tangente (elle passe dessous alors qu'elle était située au-dessus de la tangente).

Sa représentation graphique :

4. Définition et propriété du point d'inflexion

Un point d’inflexion est un point où la représentation graphique d’une fonction coupe sa tangente (et donc change de convexité).

Soit f une fonction définie sur I, deux fois dérivable sur I et soit a un réel de I.
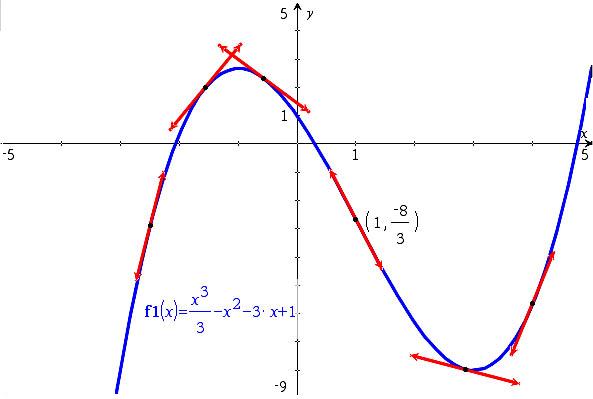
Si f ’’ s’annule pour a et change de signe, alors la représentation graphique de f admet un point d’inflexion de coordonnées (a ; f(a)).

Dans l’exemple précédent, la représentation graphique de f admet un point d’inflexion au point

5. Convexité et croissance comparée

a. Exemple

Sur l’intervalle I = [1 ; +∞[, les fonctions

sont définies dérivables deux fois.

qui est strictement négative sur I.

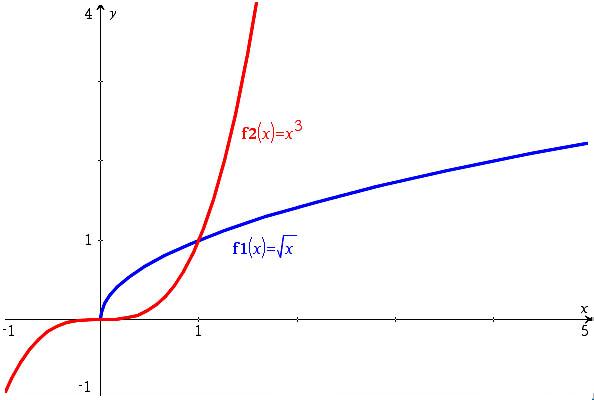
f ’’(x) strictement négative, f ’(x) strictement décroissante. Donc la fonction est concave, toujours située en dessous de ses tangentes, avec une pente de plus en plus faible.

.
Comme 1 < x nous avons g’’(x) strictement positive, g’(x) strictement croissante. Donc g est convexe, située au-dessus de toutes ses tangentes, avec une pente de plus en plus forte.

De plus, f(1) = g(1) = 1. On peut donc en conclure que pour 1 < x, on aura f(x) < g(x).

Ce que l'on constate sur la représentation graphique ci-contre :

Remarque : pour le point suivant il est nécessaire d’avoir étudié les fonctions logarithme et exponentielle.

b. Croissance comparée et positions relatives des courbes représentatives des fonctions x, logarithme et exponentielle

• La fonction

est définie sur

et est deux fois dérivable :

. Cette fonction n’est ni convexe ni concave (ou les deux si l’on veut). La pente de ses tangentes est constante et vaut 1.

• La fonction

est définie sur [0 ; +∞[, deux fois dérivable :

.

Cette fonction est concave, toujours située en-dessous de ses tangentes, avec une pente de plus en plus faible.
Au point d’abscisse x = 1, l’équation réduite de sa tangente est y = x - 1. Donc en-dessous de la droite y = x.
On peut en conclure que la courbe représentative de la fonction ln est toujours en-dessous de la droite y = x.

• La fonction

est définie sur

, deux fois dérivable :

.

Cette fonction est convexe, toujours située au-dessus de ses tangentes, avec une pente de plus en plus forte. Au point d’abscisse x = 0, l’équation réduite de sa tangente est y = x + 1. Donc au-dessus de la droite y = x.

On peut en conclure que la courbe représentative de la fonction e^x est toujours au-dessus de la droite y = x.

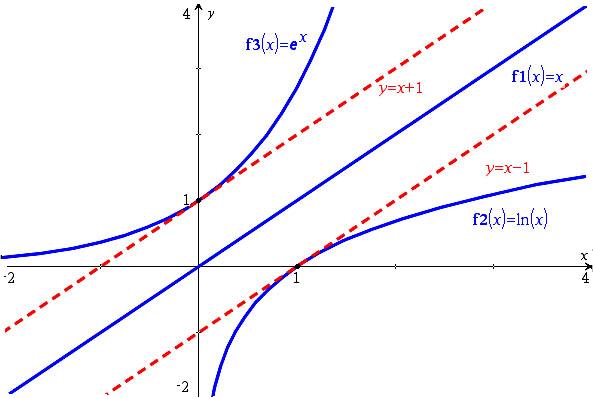
Le schéma ci-dessous permet de visualiser tout ce qui vient d'être énoncé :