Fiche de cours

Exploiter l'atténuation d'une onde sonore

Lycée > Terminale > Physique Chimie > Exploiter l'atténuation d'une onde sonore

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectifs

Exploiter l'expression qui donne le niveau d'intensité sonore du signal.
Illustrer l'atténuation géométrique et l'atténuation par absorption

Points clés

L’intensité sonore I est la puissance sonore reçue par unité de surface.
On associe l’intensité sonore au niveau sonore L par 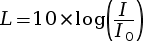, avec I₀ = 10^–¹² W·m^–², l’intensité sonore de référence.
Lorsqu’une onde sonore est émise par une source, elle parvient à un récepteur en ayant subi une atténuation géométrique et une atténuation par absorption (si un matériau se trouve entre les deux éléments).
L’atténuation A est liée à la perte d’intensité du signal lors de sa transmission.

Pour bien comprendre

Onde sonore, onde mécanique, puissance
log 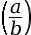= log(a) – log(b)
log(aⁿ) = n × log(a)

1. Les ondes sonores (rappels)

Une onde sonore (ou son) correspond à la propagation d’une perturbation sans transport de matière, mais avec transport d’énergie.

Pour une onde sonore qui se propage dans l’air, la perturbation consiste en des variations locales de pression. Cette variation de pression exerce une action sur les obstacles qu’elle rencontre, y compris le tympan de l’oreille, en lui transmettant une énergie.

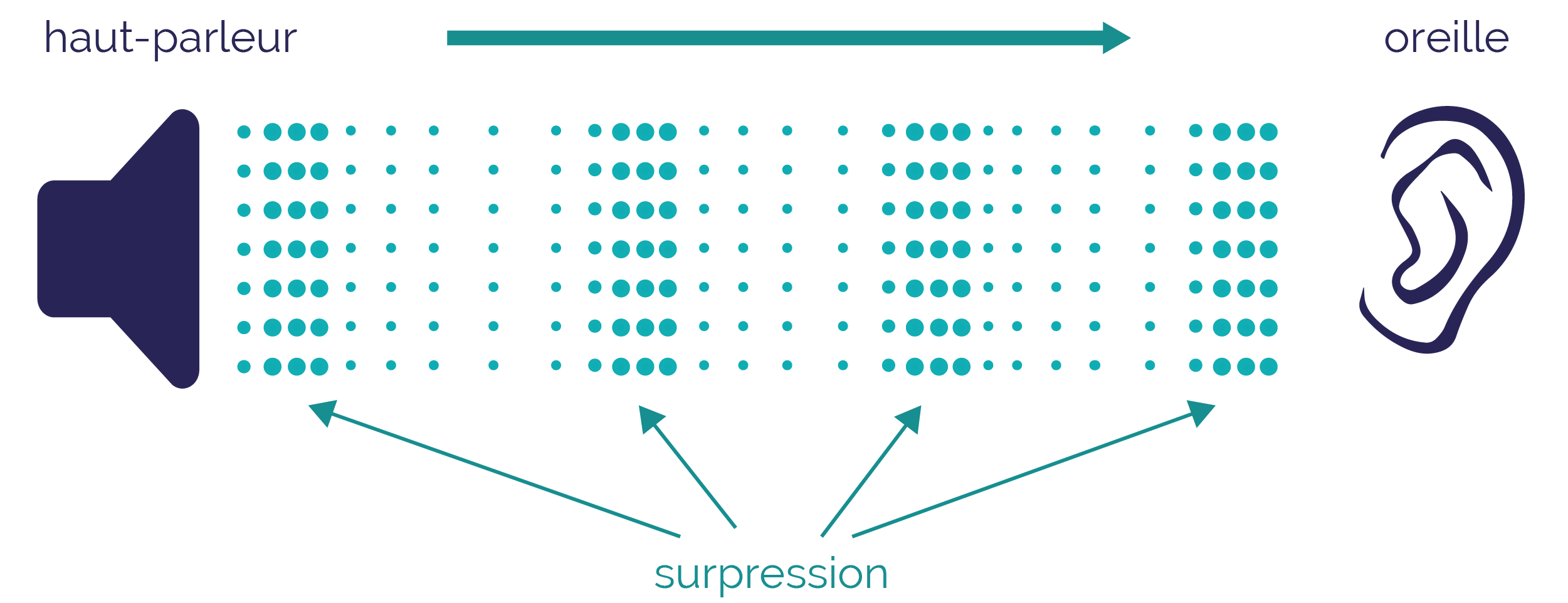
Transmission d’une onde sonore

2. Le niveau d'intensité sonore

a. Intensité sonore

Les ondes sonores véhiculent de l’énergie.

L’intensité sonore, notée I, est la puissance par unité de surface transmise par une onde sonore.

L’intensité sonore correspond donc à une puissance surfacique et s’exprime par la relation suivante.

avec :

P la puissance de l’onde sonore, en watt (W)
S la surface, en mètre carré (m²)
I l'intensité sonore, en watt par mètre carré (W·m^–²)

b. Perception des ondes sonores

Une oreille humaine est susceptible d’entendre des ondes sonores de fréquences comprises entre 20 Hz et 20 kHz.

Dans cette gamme, l’oreille est capable d’entendre une onde sonore dont l’intensité acoustique est supérieure ou égale à I₀ = 10^–¹² W·m^–².

La valeur I₀ = 10^–¹² W·m^–² correspond au seuil d’audibilité, ou intensité sonore de référence.

c. Le niveau d'intensité sonore

Lorsque plusieurs instruments de musique émettent une onde sonore, les intensités sonores dues à chaque instrument s’ajoutent, pourtant l’onde sonore résultante de cet ensemble ne correspond pas à la somme des intensités sonores.

On fait donc appel à une nouvelle grandeur qui traduit cette perception sonore : c’est le niveau sonore, noté L, qui se mesure avec un sonomètre.

Un sonomètre

Le niveau sonore L est relié à l’intensité acoustique I par la relation suivante.

avec :

L le niveau sonore, en décibel (dB)
I l’intensité sonore, en watt par mètre carré (W·m^–²)
I₀ l’intensité sonore de référence : I₀ = 10^–¹² W·m^–²
log la fonction logarithme décimal

La finalité du niveau sonore L est de comparer une intensité acoustique I (en W·m^–²) avec l’intensité acoustique du seuil d’audibilité I₀ = 10^–¹² W·m^–² en utilisant une échelle logarithmique.

Remarque
Il faut connaitre les propriétés vérifiées par le logarithme décimal.

log(10ⁿ) = n
log(1) = 0
log(10) = 1

Exemples

Si une onde sonore a une intensité sonore
I = 2 × 10^–⁵ W·m^–², son niveau d’intensité sonore vaut :
L = 10 × log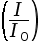= 10 × log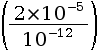
L = 10 × log(2 × 10⁷) ≈ 73 dB
Si une onde sonore a un niveau d’intensité sonore L = 85 dB, puisque 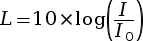, son intensité acoustique vaut :

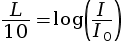
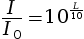
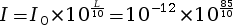≈ 3,16 × 10^–⁴ W·m^–²
Si I = I₀, alors L = 0 dB car 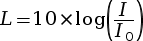= 10 × log(1) = 0 (log 1 = 0).
Si I = 10 × I₀, alors L = 10 dB car log(10) = 1.

d. Échelle de niveau d'intensité sonore

L’échelle ci-dessous donne les niveaux sonores de quelques sons courants.

Échelle des niveaux sonores

On remarque que des sons de niveaux sonores supérieurs à 85 dB sont dangereux, car ils sont potentiellement nocifs pour les oreilles. Ceux au dessus de 120 dB peuvent occasionner des pertes d’audition, parfois irréversibles. Le seuil de perception des sons est à 0 dB.

3. L'atténuation sonore

On considère un émetteur qui produit une onde sonore d’intensité sonore I. Un récepteur perçoit une intensité sonore inférieure à celle émise par l’émetteur.

La perte d’intensité sonore à son arrivée au récepteur résulte de plusieurs phénomènes d’atténuation.

L’atténuation géométrique.
L’atténuation par l’absorption d’un matériau qui se trouve entre l’émetteur et le récepteur.

a. L'atténuation géométrique

Quand une onde sonore émise par une source ponctuelle se propage dans l’air sans rencontrer d’obstacle, elle évolue selon des sphères concentriques centrées sur la source.

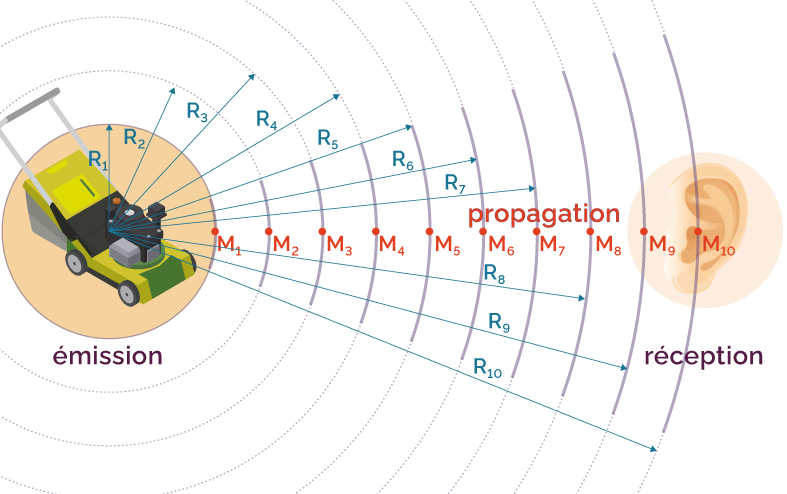
Propagation de l’onde sonore

La puissance P sonore émise par la source à un instant donné est ainsi répartie sur toute la surface S d’une sphère dont le rayon R augmente.

Or, la surface d’une sphère vaut S = 4πR² et puisque la puissance P de cette onde sonore est constante au cours du temps, l’intensité sonore va dépendre de R.

Ainsi, si l’émetteur se situe en M₂, il recevra une intensité sonore inférieure à celle reçue en M₁ car le rayon R₁ est plus petit que le rayon R₂.

L’intensité sonore décroit au fur et à mesure que l’on s’éloigne d’une source, c’est l’atténuation géométrique.

b. L'atténuation par absorption

Lorsqu’une onde sonore rencontre un matériau (incidence supposée normale à la paroi), l’onde transporte une intensité sonore I_incidente, dont :

une partie est réfléchie et transporte une intensité sonore I_réfléchie ;
une partie est absorbée par le matériau et transporte une intensité sonore I_absorbée ;
une partie est transmise par la matériau et transporte une intensité sonore I_transmise.

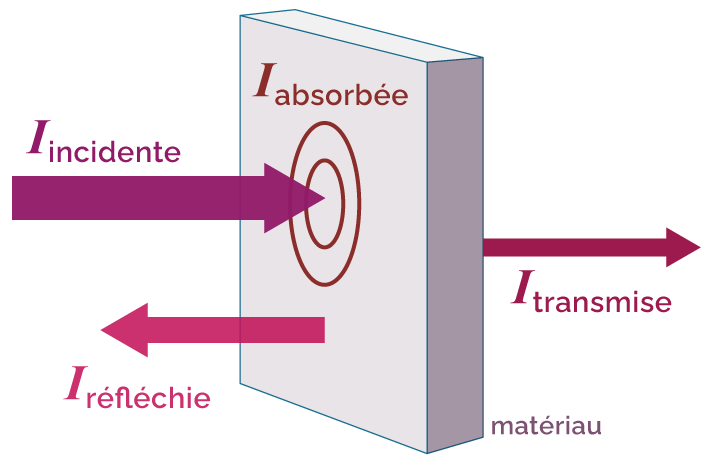
Trajet du son au contact d’un matériau

L’atténuation d’une onde sonore incidente, après la traversée du matériau, se traduit par une baisse de l’intensité sonore.

On appelle l'atténuation A la grandeur définie par la relation suivante.

avec :

A l’atténuation, en décibel (dB)
I_incidente l’intensité sonore incidente, en watt par mètre carré (W·m^–²)
I_transmise l’intensité sonore transmise par le matériau, en watt par mètre carré (W·m^–²)

Remarques

Comme I_transmise≤ I_incidente, l’atténuation A est forcément positive ou nulle.
Si I_incidente = I_transmise, alors l’atténuation A est nulle (cas de la transmission idéale, sans perte).

Évalue ce cours !

Note 4.2 / 5. Nombre de vote(s) : 125

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT