Étudier une lunette afocale
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Représenter le schéma d’une lunette afocale modélisée par deux lentilles minces convergentes ; identifier l’objectif et l’oculaire.
- Représenter le faisceau émergent issu d'un point objet situé « à l’infini » et traversant une lunette afocale.
- Établir l’expression du grossissement d’une lunette afocale.
- Une lunette astronomique est un dispositif optique qui permet d’obtenir l’image grossie d’un objet lumineux qui est très éloigné.
- La lunette astronomique est composée de deux
lentilles convergentes.
- L’objectif qui forme une image intermédiaire d’un objet situé à l’infini.
- L’oculaire qui, à partir de l’image intermédiaire, forme une image à l’infini observable par l’œil.
- Le foyer image de l’objectif est confondu avec le foyer objet de l’oculaire : la lunette astronomique est un système afocal.
- L’angle (ou diamètre) apparent d’un
objet est égal à l’angle sous lequel on
voit cet objet placé à l’infini.
Le grossissement de la lunette astronomique est égal au rapport de l’angle apparent de l’objet vu à travers la lunette sur celui de l’objet vu à l’œil nu.
Le grossissement est également égal au rapport de la distance focale de l’objectif sur celui de l’oculaire.
- Lentille convergente, foyer, rayons particuliers
- Formule de la tangente dans un triangle rectangle
La lunette astronomique est composée de deux lentilles convergentes : l’objectif et l’oculaire.
La lentille convergente est un système optique composé par l’intersection de deux sphères : elle possède des bords minces et un centre bombé.
Elle est caractérisée par son centre optique O, son foyer objet F et son foyer image F', tous placés sur l’axe optique (axe de symétrie de la lentille).
On définit la distance focale f comme la distance commune OF ou OF'. Il existe des rayons particuliers dont la traversée de la lentille donne un rayon émergent caractéristique.
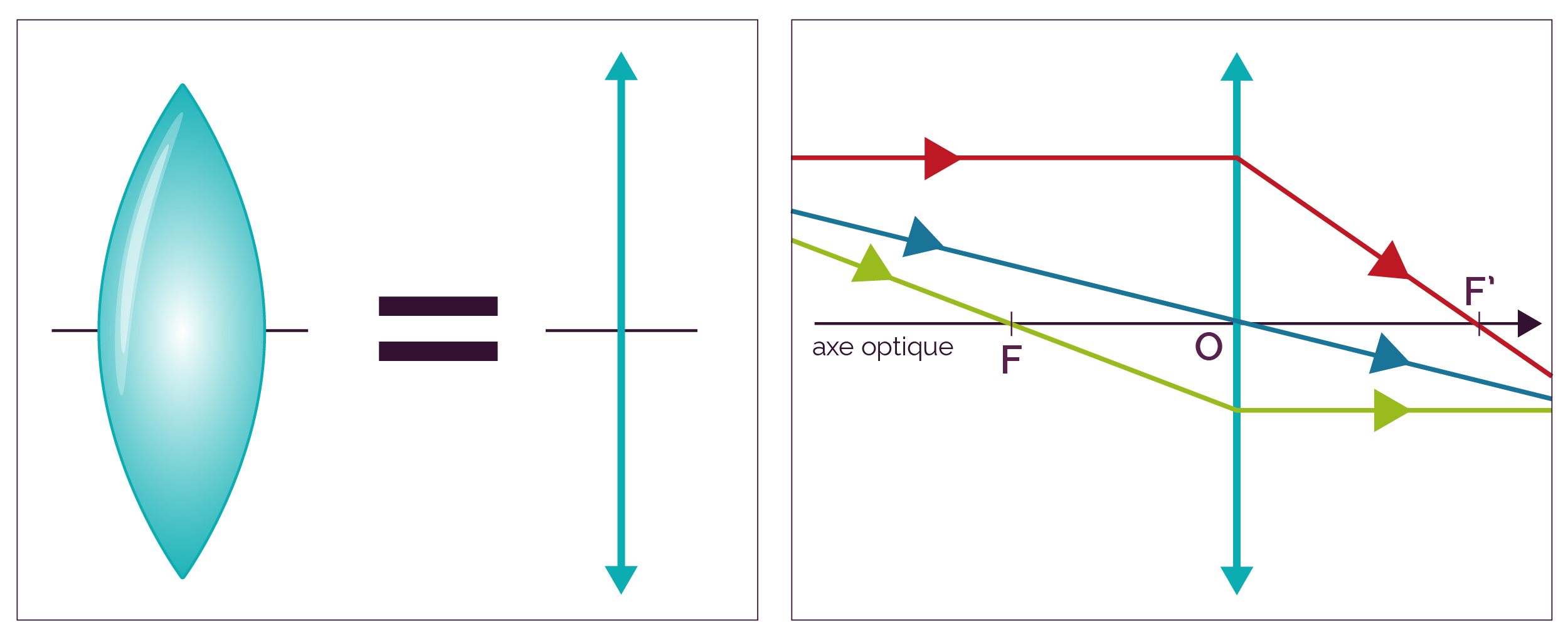
Modèle de la lentille convergente et tracé des rayons particuliers
On considère un objet AB à l’infini dont les rayons de lumière émis arrivent sur l’objectif.
L’objet lumineux étant à l’infini, tous les rayons qui viennent du point B sont parallèles entre eux lors de leur arrivée sur l’oculaire.
On peut construire l’image A1B1 de cet objet AB à l’infini par l’objectif pour lequel on notera F1 et F1' les foyers objet et image, et O1' le centre optique.
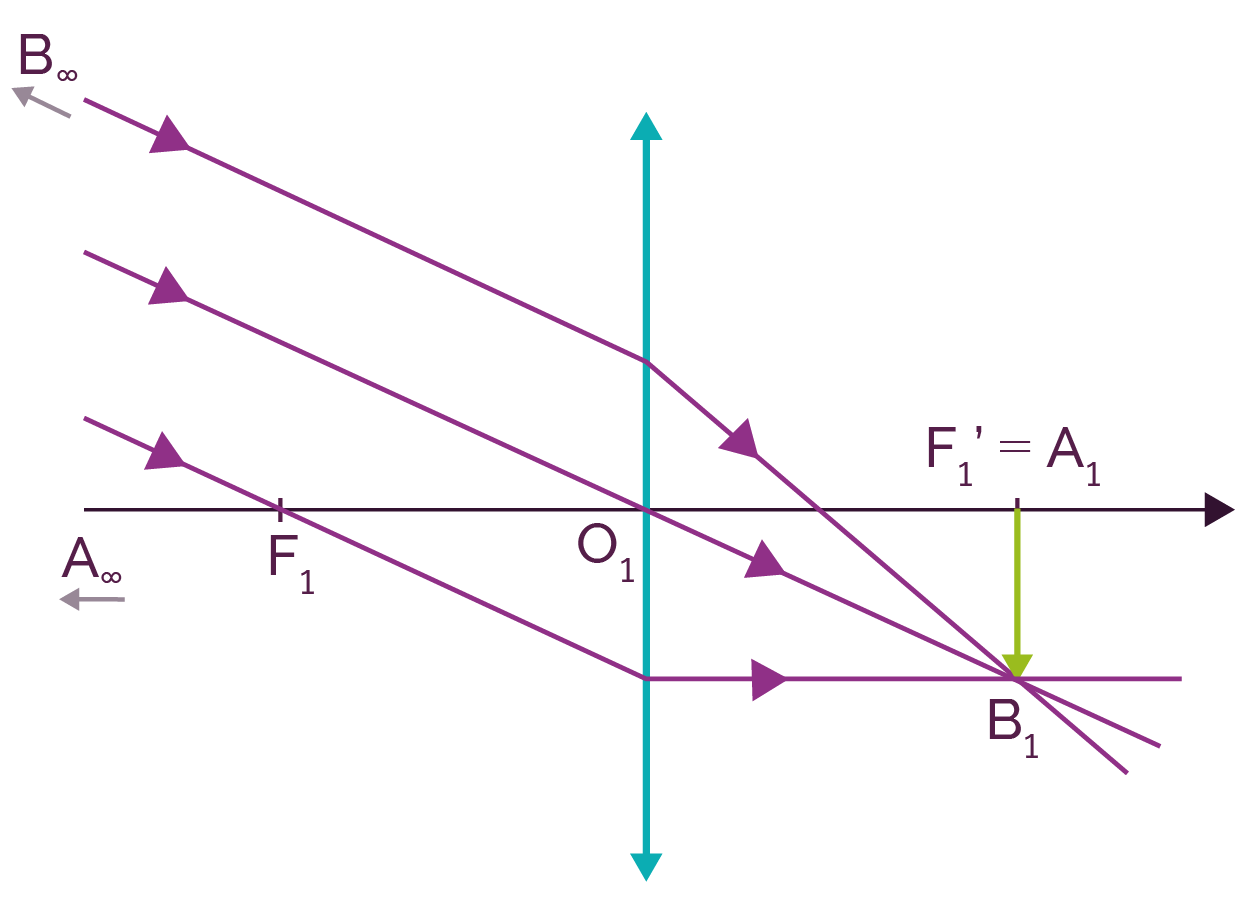
Construction de l’image intermédiaire A1B1
À partir de l’image intermédiaire A1B1, l’oculaire donne une image qui est observable : l’image A'B' formée par l’oculaire se trouve à l’infini.
La vision se fait sans accommodation dans ces conditions : l’œil ne force pas.
On peut construire l’image A'B' de l’image intermédiaire A1B1 par l’oculaire pour lequel on notera F2 et F2' les foyers objet et image, et O2' le centre optique.
L’image intermédiaire est placée dans le plan focal objet de l’oculaire (A1 et F2 sont confondus).
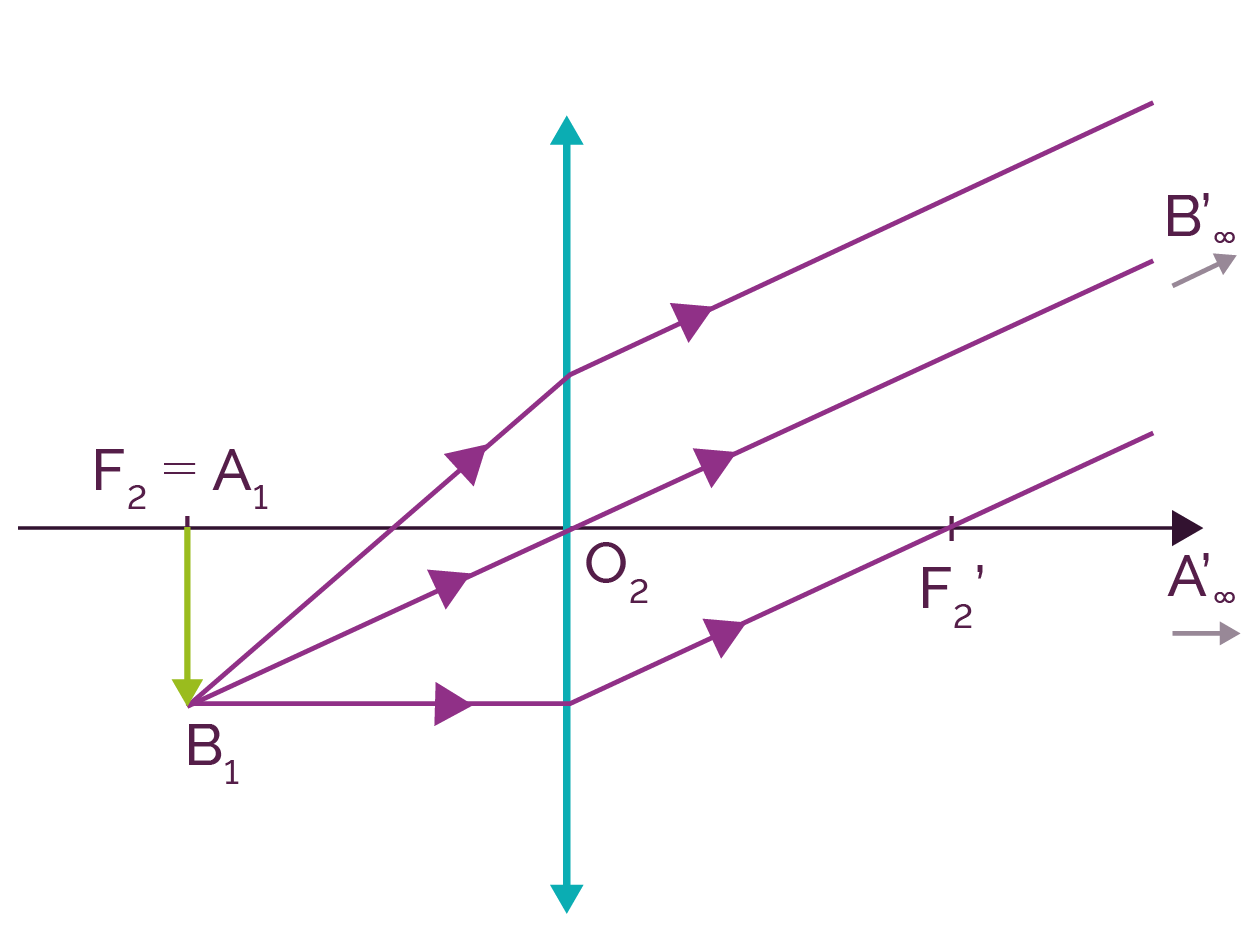
Construction de l’image définitive A'B'
Dans la lunette astronomique, le foyer image F1' de l’objectif est confondu avec le foyer objet F2 de l’oculaire.
Dans de telles conditions, on dit que la lunette astronomique est un système afocal.
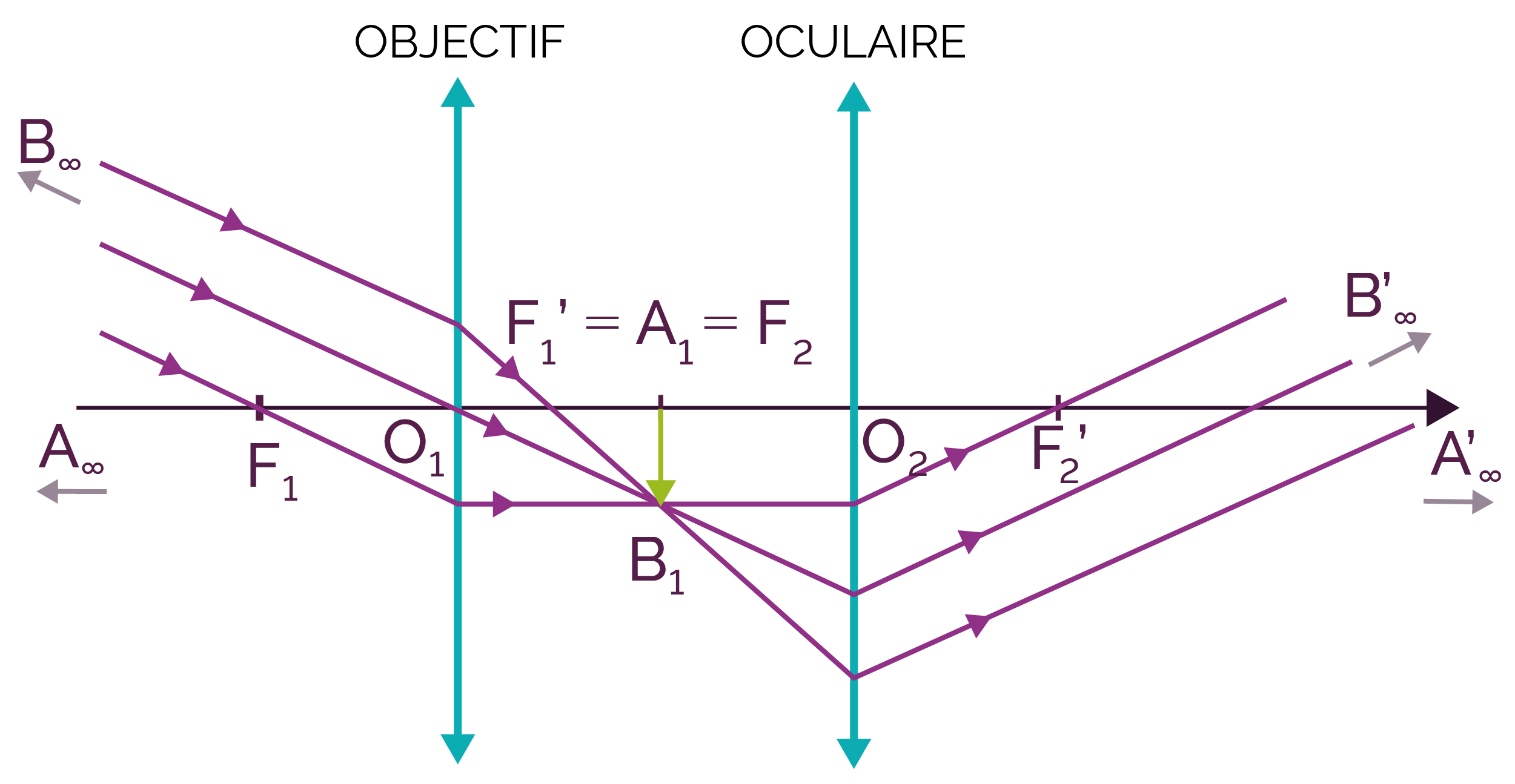
Trajets des rayons à travers
une lunette astronomique
Une lunette astronomique permet d’obtenir l’image grossie d’un objet lumineux très éloigné de nous et que l’on voit à l’œil nu sous la forme d’un petit point lumineux.
L’angle apparent d’un objet éloigné correspond à l’angle α sous lequel on voit l’objet à l’œil nu.
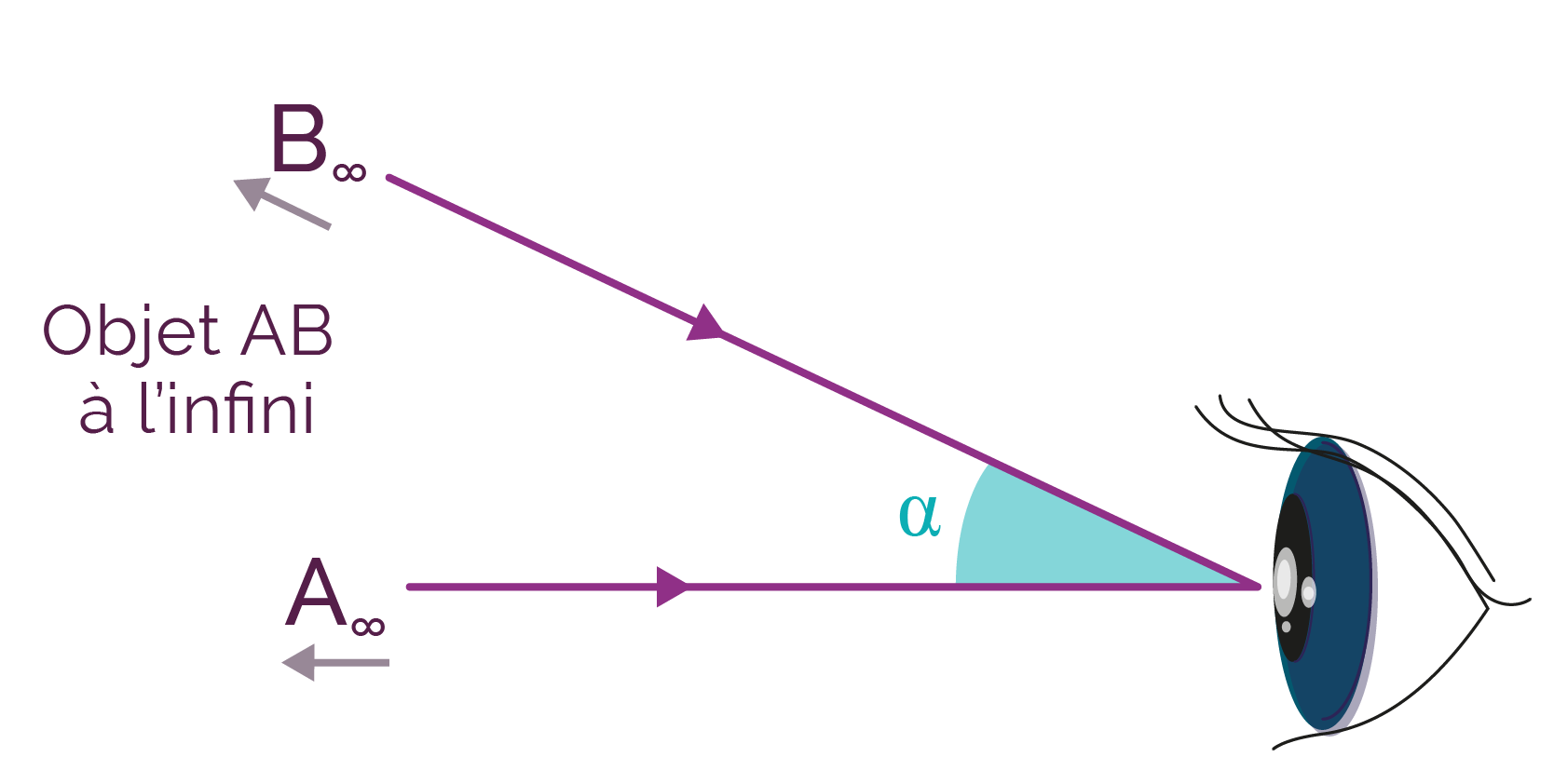
Angle apparent d’un objet placé à l’infini
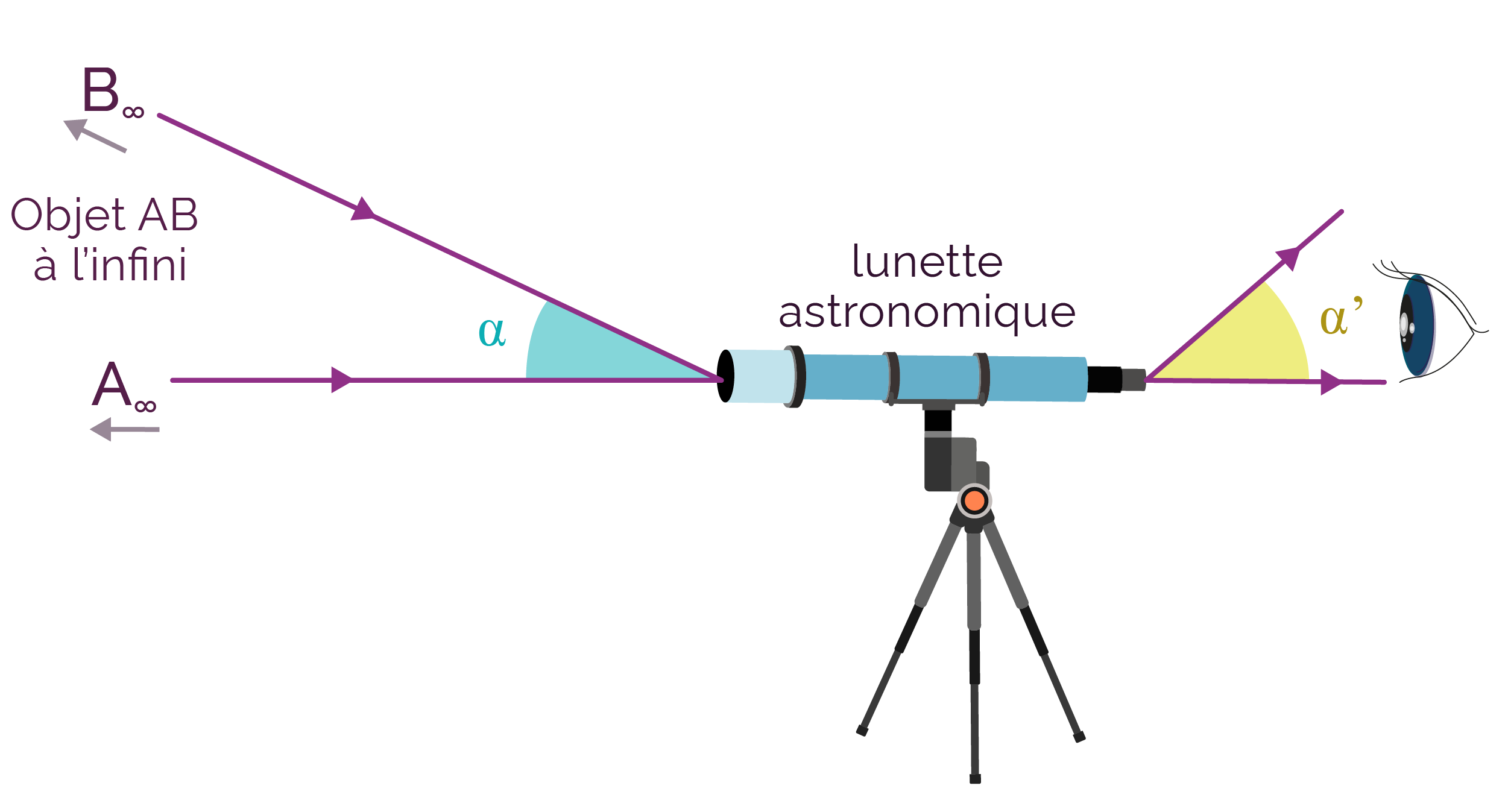
Angles apparents avant et après
la lunette astronomique
Le grossissement G a l’expression suivante.
|
|
avec :
|
L’angle apparent α' est plus grand que l’angle apparent α, le grossissement est donc strictement supérieur à 1.
On considère un rayon lumineux issu du point objet B et qui traverse la lunette astronomique.
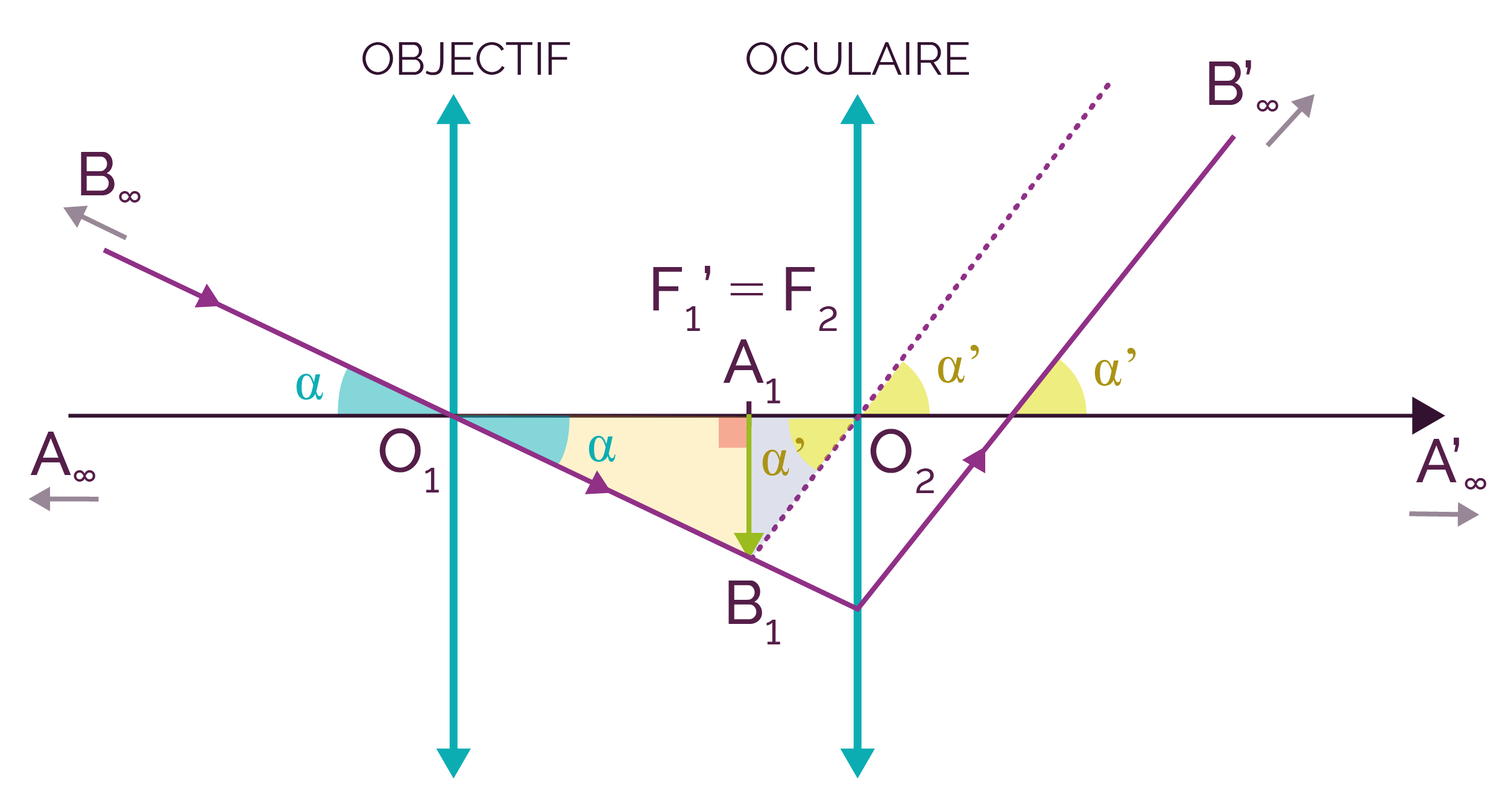
Trajet d’un rayon lumineux
à travers la lunette astronomique
On constate que les triangles suivants sont des triangles rectangles.
- Le triangle O1A1B1 rectangle en A1.
- Le triangle O2A1B1 rectangle en A1.
On applique la formule de la tangente dans ces deux triangles.
- Dans le
triangle O1A1B1 :
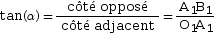
- Dans le
triangle O2A1B1 :
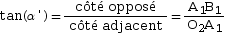
Les angles apparents sont petits (car les rayons lumineux sont peu inclinés par rapport à l’axe optique de la lunette astronomique), on peut donc appliquer l’approximation des petits angles.
tan(α) ≈ α et tan(α') ≈ α'
On obtient alors les expressions suivantes des deux angles apparents.
![]()
On fait intervenir les distances focales de l’objectif (car A1 est confondu avec F1') et de l’oculaire (car A1 est confondu avec F2) : O1A1 = f1' et O2A1 = f2'.
On obtient :
![]()
On calcule le grossissement G.
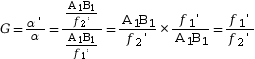
Le grossissement peut donc s’exprimer en fonction des distances focales de l’objectif et de l’oculaire.
|
|
avec :
|
La distance focale de l’objectif est de l’ordre du mètre tandis que celle de l’oculaire est de l’ordre du centimètre : cela donne donc un grossissement supérieur à 1.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








