Lycée > Terminale > Physique Chimie > Étudier le modèle capacitif

Étudier le modèle capacitif

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectif

Relier l’intensité d’un courant électrique au débit de charges, c’est-à-dire à la charge électrique qui traverse une section droite d’un conducteur métallique.

Points clés

Un condensateur est un dipôle électrique qui est constitué de deux surfaces métalliques (appelées armatures) séparées par un isolant électrique.
La capacité d’un condensateur (exprimée en farad F) mesure la possibilité pour un condensateur d'accumuler un plus grand nombre de charges électriques de signes opposés sur chacune de ses armatures. Pour une tension fixée aux bornes du condensateur, la charge électrique accumulée augmente avec la capacité. Les charges électriques portées par chaque armature sont opposées.
Les capacités usuelles des condensateurs sont de l’ordre du nanofarad jusqu’au microfarad.
Les relations qui lient l’intensité du courant i, la charge électrique q_A d’une armature A et la tension aux bornes du condensateur u_AB sont 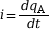, 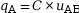et .

Pour bien comprendre

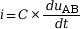Dérivée d’une fonction

1. Le condensateur

Un condensateur est un dipôle qui a la propriété de pouvoir emmagasiner de l’énergie électrique et de pouvoir la restituer sur des durées très petites : il est donc capable d’alimenter des dispositifs qui nécessitent une grande puissance électrique sur de courtes durées (lampe flash d’un appareil photographique, stimulateur cardiaque, etc.).

Le modèle capacitif (modélisation du condensateur) peut être étendu aux accélérateurs de particules.

a. Composition et grandeurs électriques du condensateur

Composition

Un condensateur est un dipôle constitué de deux armatures métalliques, chacune reliée à une des bornes et séparées par un isolant électrique qui est appelé diélectrique.

Exemples de condensateurs et symbole normalisé

Grandeurs électriques

Le condensateur est caractérisé par quelques grandeurs électriques.

q_A et q_B sont les charges électriques (en coulomb C) portées respectivement par chacune des armatures A et B du condensateur.
u_AB est la tension électrique (en volt V) aux bornes du condensateur.
i est l’intensité du courant (en ampère A) qui traverse le condensateur.

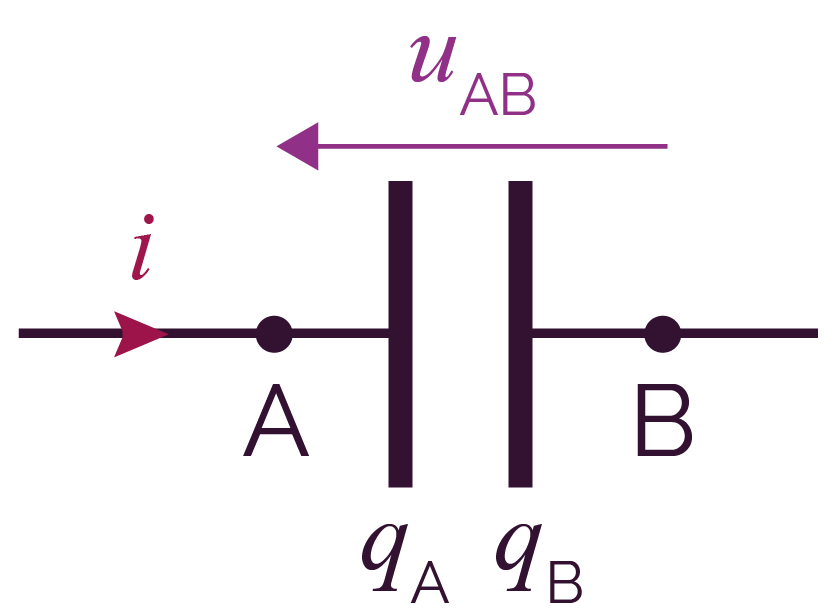
Grandeurs électriques associées au condensateur

b. La capacité d'un condensateur

Lorsqu’un courant électrique circule et traverse un condensateur, des charges électriques de signes opposés s’accumulent sur chacune des armatures du condensateur.

Lorsque la charge électrique maximale que peut accepter chacune des armatures est atteinte, le courant ne peut plus traverser le condensateur qui se comporte alors comme un interrupteur ouvert.

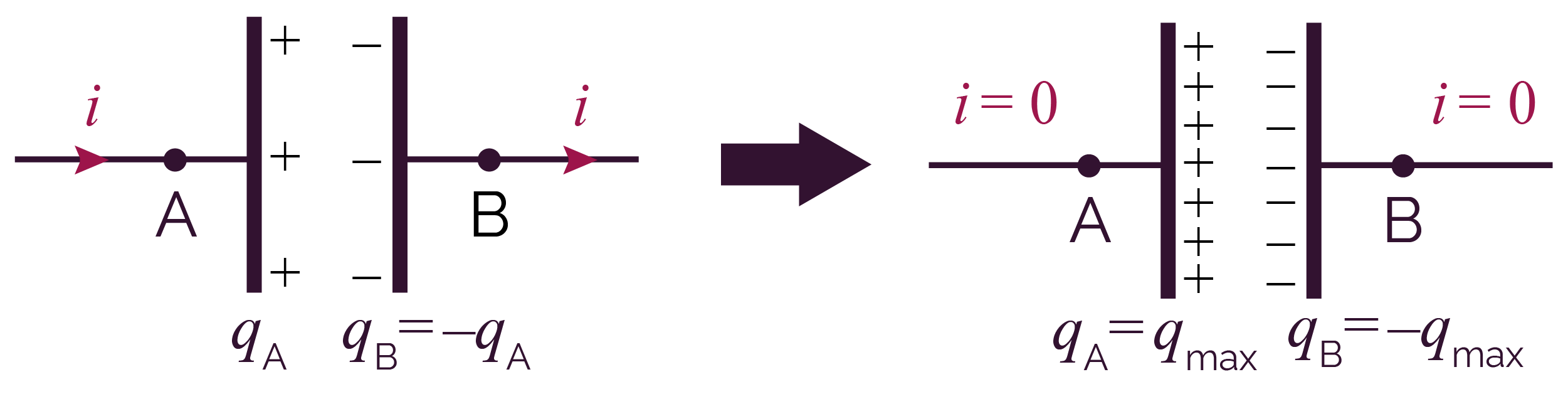
Charge électrique du condensateur

La capacité d’un condensateur correspond à l’aptitude de celui-ci à accumuler sur ses armatures un grand nombre de charges électriques. On la note C et son unité est le farad (F).

Remarque
Les condensateurs ont souvent des capacités de quelques microfarads (1 μF = 1 × 10^–⁶ F) ou nanofarads (1 nF = 1 × 10^–⁹ F).

La tension u_AB aux bornes du condensateur est proportionnelle à la charge électrique de l’une de ses armatures, avec la capacité C qui est le coefficient de proportionnalité.

q_A = C × u_ABet q_B = –C × u_AB

avec :

q_A ou q_B la charge électrique accumulée sur l’armature A ou B du condensateur, en coulomb (C)
u_AB la tension aux bornes du condensateur, en volt (V)
C la capacité du condensateur, en farad (F)

Pour une tension fixée, la charge électrique q accumulée sur l’armature du condensateur est d’autant plus grande que la valeur de la capacité C est grande.

2. La relation entre l'intensité du courant électrique et la tension aux bornes d'un condensateur

Lorsque le condensateur est traversé par un courant électrique, des charges électriques apparaissent sur chacune de ses armatures et elles sont de valeurs opposées.

Il existe un lien entre l’intensité i du courant électrique et la charge électrique q_A de l’armature du condensateur.

a. L'intensité du courant

Le courant électrique dans un conducteur métallique correspond à un mouvement d’ensemble des électrons libres du métal.

En régime permanent (indépendant du temps)

En régime permanent, c’est-à-dire qui est indépendant du temps, l’intensité du courant I en un point d’un circuit est égale à la charge électrique Q qui traverse la section droite du conducteur par unité de temps Δt.

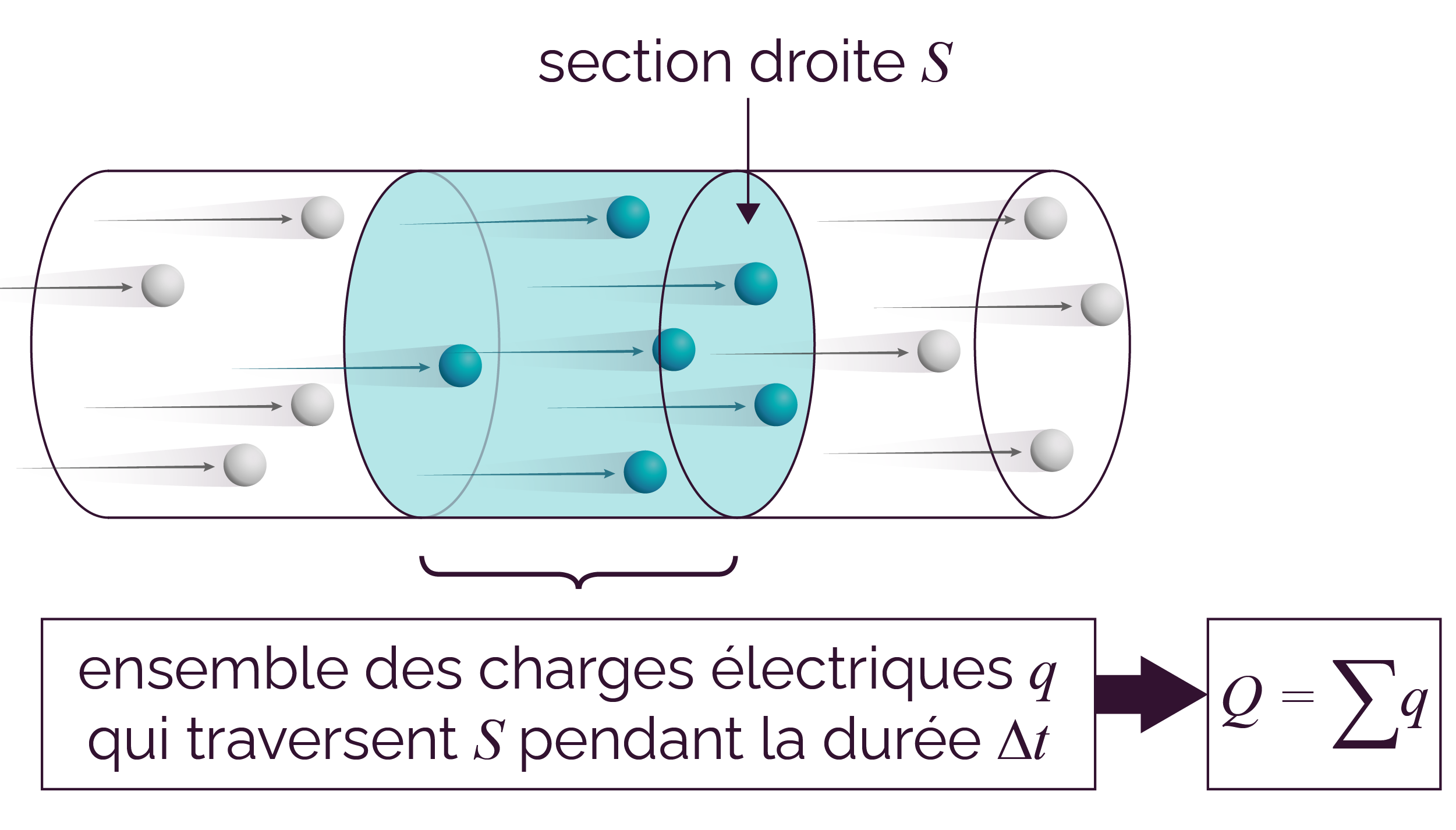
Circulation des charges électriques dans un conducteur métallique

L’expression de l’intensité du courant I est la suivante.

avec :

I l’intensité du courant, en ampère (A)
Q la charge électrique qui traverse la section droite d’un condensateur, en coulomb (C)
Δt la durée écoulée, en seconde (s)

Remarque
Un ampère correspond à un coulomb par seconde.

En régime variable (dépendant du temps)

En régime variable, c’est-à-dire qui dépend du temps, l’intensité du courant i est égale à la dérivée temporelle de la charge électrique q(t).

avec :

i l’intensité du courant, en ampère (A)
q(t) la charge électrique qui traverse la section droite d’un condensateur, à un instant donné, en coulomb (C)
t l'instant étudié, en seconde (s)

b. La relation entre l'intensité et la tension

On considère un condensateur qui est traversé par un courant d’intensité i(t).

Ce courant est orienté de telle sorte qu’il arrive sur l’armature A.

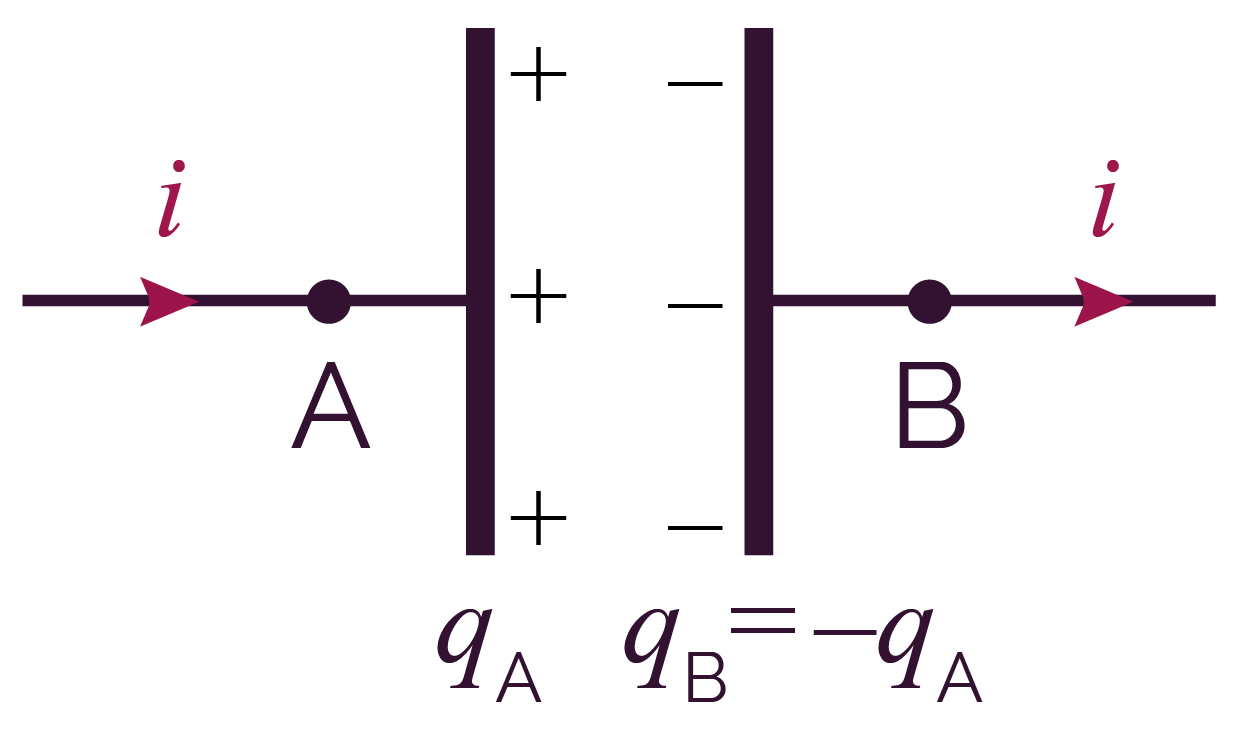
Traversée d’un condensateur par un courant

La relation entre i(t) et q_A est la suivante.

avec :

i l’intensité du courant, en ampère (A)
q_A la charge électrique, en coulomb (C)
t l’instant étudié, en seconde (s)

Remarque
Comme le courant part de l’armature B, il faut mettre un signe moins devant la dérivée si l’on fait intervenir la charge électrique q_B.

Dans cette relation, on remplace la charge électrique q_A par son expression en fonction de la tension u_AB.

La relation établie est donc la suivante.

avec :

i l’intensité du courant, en ampère (A)
u_AB la tension aux bornes du condensateur, en volt (V)
t l’instant étudié, en seconde (s)
C la capacité du condensateur, en farad (F)

On constate que :

si u_ABdiminue, alors 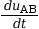est négative :
i(t) est négatif donc le courant part de l’armature A ;
si uAB augmente, alors 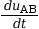est positive :
i(t) est positif donc le courant arrive sur l’armature A.