Vitesse volumique et temps de demi-réaction
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- À partir de données expérimentales, déterminer une vitesse volumique de disparition d’un réactif, une vitesse volumique d’apparition d’un produit ou un temps de demi-réaction.
- À partir de données expérimentales, identifier si l’évolution d’une concentration suit ou non une loi de vitesse d’ordre 1.
- La vitesse volumique est la dérivée
temporelle de la concentration de
l’espèce.
La vitesse volumique d’apparition vProduit est égale à la dérivée temporelle de la concentration des produits, et la vitesse volumique de disparition vRéactif est égale à l’opposé de cette dérivée temporelle pour les réactifs. - Le temps de demi-réaction t1/2 est égal à la durée au bout de laquelle la quantité initiale de réactif limitant (ou sa concentration initiale) a été divisée par deux.
- Une réaction chimique suit une loi de vitesse d’ordre 1 par rapport à un réactif ou à un produit, si la vitesse volumique d’apparition du produit ou de disparition du réactif est proportionnelle à la concentration en quantité de matière du produit ou du réactif.
- Concentration en quantité de matière
- Réaction chimique : réactif limitant
- Dérivée d’une fonction, coefficient directeur
On peut étudier l’évolution des transformations chimiques en s’intéressant à leurs caractéristiques cinétiques : vitesse volumique de disparition d’un réactif, vitesse volumique d’apparition d’un produit et temps de demi-réaction.
Lors d’une réaction chimique, des réactifs sont consommés et des produits sont formés au cours du temps, entre le début (qui correspond à la mise en présence des réactifs) et la fin (qui correspond à l’instant où les quantités de matière ou les concentrations des réactifs ou des produits n’évoluent plus).
À partir des courbes d’évolution temporelle des concentrations des réactifs ou des produits, on peut déterminer la vitesse volumique d’apparition d’un produit ou de disparition d’un réactif au cours de la réaction chimique.
La vitesse volumique de disparition d’un réactif vRéactif se calcule à partir de la dérivée temporelle de la concentration en quantité de matière du réactif, notée [R].
|
avec :
|
La notation d’une dérivée en mathématiques se fait à l’aide d’un prime (').
En physique, la notation de cette même dérivée se fait avec une différentielle où la variable sur laquelle on réalise la dérivée est précisée au dénominateur.
Notation mathématique → 
← Notation
différentielle
Dans le cas où le volume du milieu réactionnel V est indépendant du temps, on peut faire sortir ce volume de la dérivée et obtenir une autre expression.
|
|
avec :
|
La vitesse de disparition vRéactif doit être positive.
La dérivée temporelle de la concentration est négative car la concentration du réactif diminue (il est consommé). On met donc un signe moins devant cette dérivée dans la formule de la vitesse volumique de disparition.
La vitesse volumique d’apparition d’un produit vProduit se calcule à partir de la dérivée temporelle de la concentration en quantité de matière du produit, notée [P].
|
avec :
|
Dans le cas où le volume du milieu réactionnel V est indépendant du temps, on peut le faire sortir de la dérivée et obtenir une autre expression.
|
|
avec :
|
L’unité de la vitesse volumique dépend des unités de la concentration en quantité de matière et du temps.
|
Unité de la
concentration en quantité de matière |
|
|
|
| Unité du temps |
|
|
|
| Unité de la vitesse volumique |
|
|
|
À partir des courbes d’évolution temporelle des concentrations d’un réactif [R] ou d’un produit [P], on peut déterminer graphiquement les vitesses volumiques de disparition ou d’apparition.
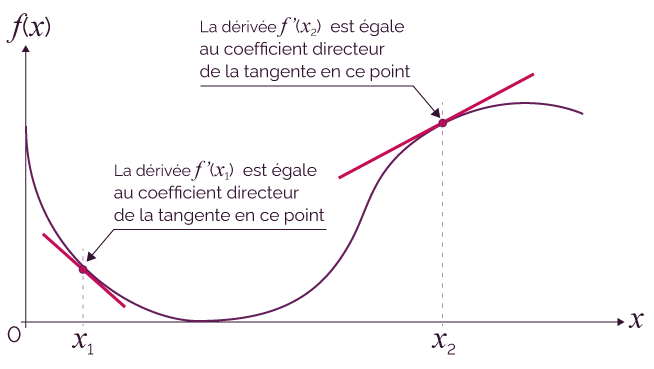
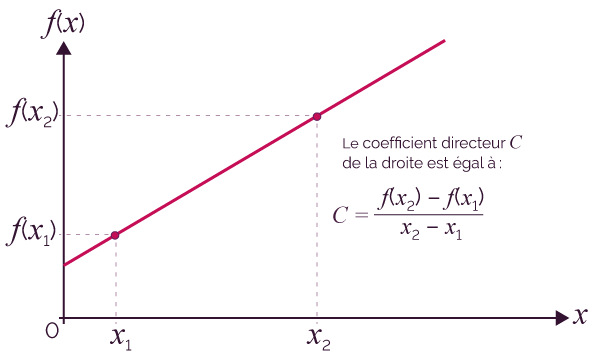
Le nombre dérivé f ’(x) en un point x d’une courbe représentant une fonction f (x) est égal au coefficient directeur de la tangente à la courbe en ce point.
On étudie la vitesse de disparition des ions thiosulfate.
La réaction entre l’ion
oxonium H3O+ et l’ion
thiosulfate S2O
produit de
l’eau H2O, du dioxyde de
soufre SO2 et du soufre S.
L’équation de la réaction chimique est la suivante.
2 H3O+ (aq) + S2O
(aq) → S (s) + SO2 (aq) + 3 H2O (l)
C’est une réaction lente et on trace l’évolution de la concentration de l’ion thiosulfate au cours du temps.
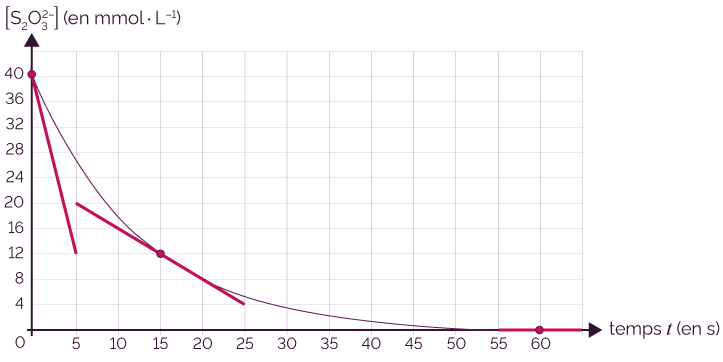
Évolution de la concentration de l’ion thiosulfate
au cours du temps
On représente les tangentes à la courbe aux instants t = 0 s, t = 15 s et t = 60 s.
- On calcule la vitesse volumique de disparition
à l’instant
t = 0 s.
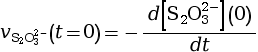
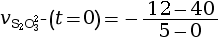
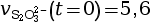mmol·L–1·s–1
- On calcule la vitesse volumique de disparition
à l’instant
t = 15 s.
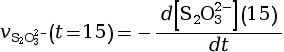
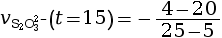
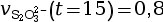mmol·L–1·s–1
- On calcule la vitesse volumique de disparition
à l’instant
t = 60 s.
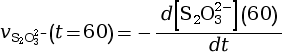
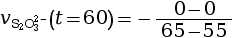
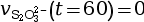mmol·L–1·s–1
On constate que la valeur de la vitesse volumique de disparition diminue de manière continue au cours du temps et tend vers la valeur zéro : elle devient nulle lorsque la réaction est terminée.
On étudie la vitesse d’apparition du dioxyde de soufre.
La réaction entre l’ion
oxonium H3O+ et l’ion
thiosulfate S2O produit de
l’eau H2O, du dioxyde de
soufre SO2 et du soufre S.
L’équation de la réaction chimique est la suivante.
2 H3O+ (aq) + S2O (aq) → S (s) + SO2 (aq) + 3 H2O (l)
C’est une réaction lente et on trace l’évolution de la concentration en dioxyde de soufre au cours du temps.
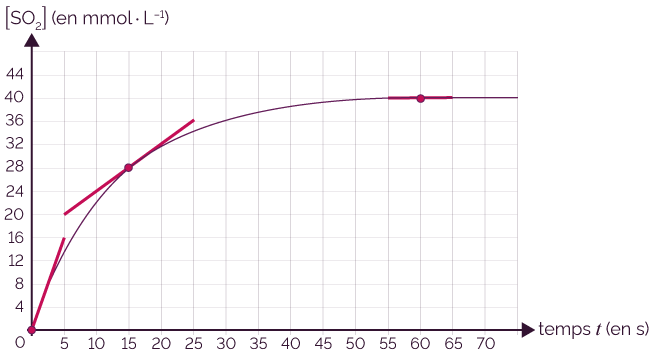
Évolution de la concentration du dioxyde de soufre
au cours du temps
On représente les tangentes à la courbe aux instants t = 0 s, t = 15 s et t = 60 s.
- On calcule la vitesse volumique d’apparition
à l’instant
t = 0 s.
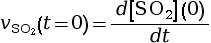
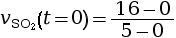
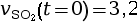mmol·L–1·s–1
- On calcule la vitesse volumique d’apparition
à l’instant
t = 15 s.
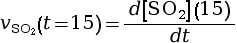
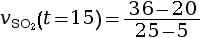
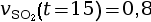mmol·L–1·s–1
- On calcule la vitesse volumique d’apparition
à l’instant
t = 60 s.
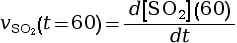
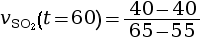
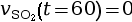mmol·L–1·s–1
On constate que la valeur de la vitesse volumique d’apparition diminue de manière continue au cours du temps et tend vers la valeur zéro : elle devient nulle lorsque la réaction est terminée.
La loi de vitesse d’ordre 1 pour un réactif est la suivante.
| vRéactif = kR × [R] |
avec :
|
La loi de vitesse d’ordre 1 pour un produit est la suivante.
| vProduit = kP × [P] |
avec :
|
Voici la méthode pour déterminer si une réaction chimique obéit à une loi de vitesse d’ordre 1.
- À partir d’une courbe d’évolution temporelle de la concentration d’un réactif ou d’un produit, on calcule la vitesse volumique de disparition ou d’apparition.
- On trace ensuite la courbe de la vitesse volumique en fonction de la concentration en quantité de matière.
- Si la courbe obtenue est une droite passant par l’origine, alors la réaction chimique obéit à une loi de vitesse d’ordre 1 par rapport au réactif ou au produit.
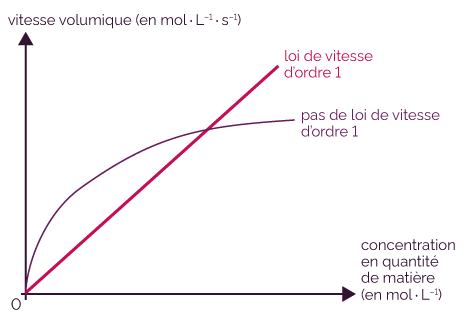
Mise en évidence d’une loi de vitesse d’ordre 1
C’est donc la durée au bout de laquelle la concentration en quantité de matière initiale du réactif limitant a été divisée par deux.
Le réactif limitant est le réactif dont la quantité de matière à la fin de la réaction est nulle. L’autre réactif est dit en excès. On peut l’identifier à partir des courbes d’évolution temporelle des quantités de matière (ou des concentrations en quantité de matière).
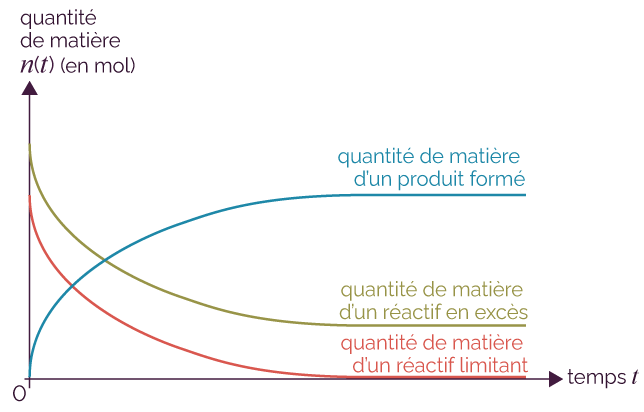
Évolution des quantités de matière
des réactifs et des produits
La détermination graphique du temps de demi-réaction se fait à partir de la courbe d’évolution temporelle de la quantité de matière (ou de la concentration) du réactif limitant.
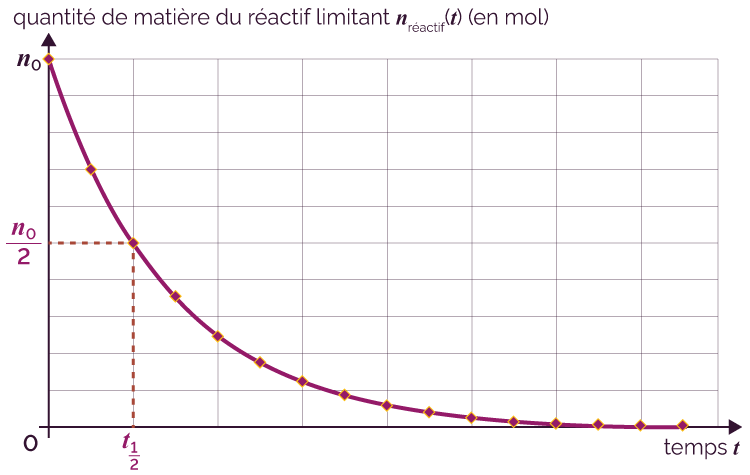
Détermination graphique du temps de demi-réaction
Une réaction est d’autant plus lente que son temps de demi-réaction est grand.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Fermer
Accédez gratuitement à
