Exploiter le phénomène d'interférences
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Caractériser le phénomène d’interférences de deux ondes et en citer des conséquences concrètes.
- Établir les conditions d’interférences constructives et destructives de deux ondes issues de deux sources ponctuelles en phase dans le cas d'un milieu de propagation homogène.
- Prévoir les lieux d’interférences constructives et les lieux d’interférences destructives dans le cas des trous de Young, l’expression linéarisée de la différence de chemin optique étant donnée. Établir l’expression de l’interfrange.
- Le phénomène d’interférences résulte de la superposition de deux ondes de même fréquence (synchrones) et de déphasage constant entre elles (cohérentes).
- Dans l’expérience des trous de Young, deux
trous éclairés par une radiation de longueur
d’onde λ donnent naissance à
deux ondes synchrones et cohérentes. Des franges
d’interférences sont alors observables sur un
écran. Selon la valeur de la différence de
marche δ, il
y a deux configurations particulières :
- Si δ = k × λ, les ondes sont en phase, les interférences sont constructives : franges brillantes ;
- Si
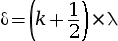 , les ondes sont en
opposition de phase, les interférences sont
destructives : franges sombres.
, les ondes sont en
opposition de phase, les interférences sont
destructives : franges sombres.
- La différence de marche s’exprime par
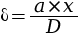 avec a la distance entre les deux
trous en mètre, et D la distance qui sépare
les trous et l’écran.
avec a la distance entre les deux
trous en mètre, et D la distance qui sépare
les trous et l’écran.
- L’interfrange (noté i) entre deux franges brillantes consécutives est constant dans ce montage.
- Onde, diffraction
- Fréquence d'une onde, retard, longueur d'onde
Une onde (mécanique ou électromagnétique) possède une périodicité dans l’espace : la longueur d’onde λ. Cette grandeur caractérise l'onde.
L’ensemble des points de l’onde situés à la même distance de la source émettrice constituent un front d’onde. La distance minimale entre deux fronts d’onde est la longueur d’onde λ. C’est par exemple la distance entre deux vagues consécutives lorsqu’on fait tomber une goutte dans l’eau (l’onde est alors mécanique).

Figure obtenue après la tombée
d’une goutte dans l’eau
On étudie maintenant ce qu’il se passe si on fait tomber en même temps deux gouttes identiques dans l’eau.

Figure obtenue après la tombée
de deux gouttes d’eau
Lorsque les deux ondes se rencontrent, il y a des endroits où la perturbation résultante est minimale et d’autres endroits où elle est maximale.
La perturbation qui résulte de la rencontre de ces deux ondes est appelée interférence.
Ces interférences sont dites :
- constructives lorsque l’onde résultante a une amplitude maximale ;
- destructives lorsque l’onde résultante a une amplitude minimale.
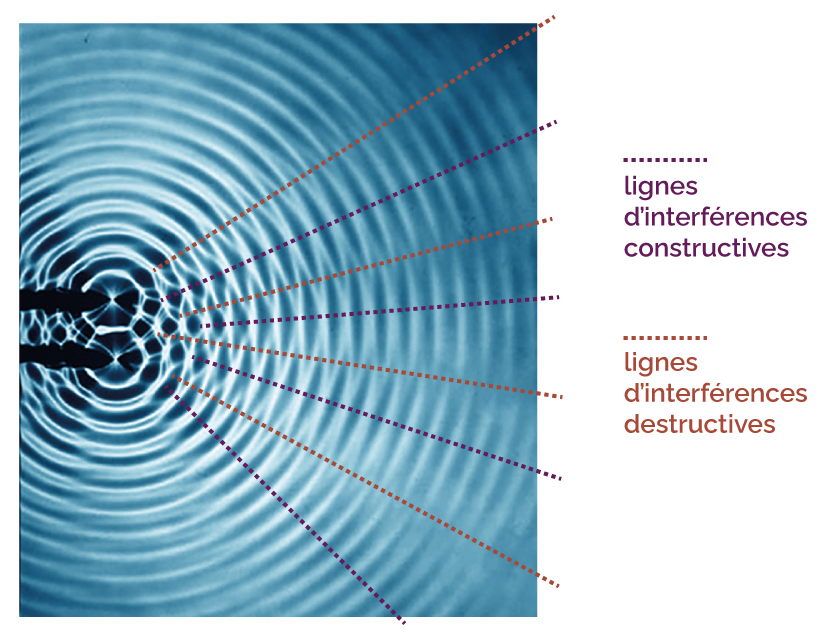
Interprétation de la figure obtenue
On étudie le schéma suivant pour interpréter le phénomène d’interférences.
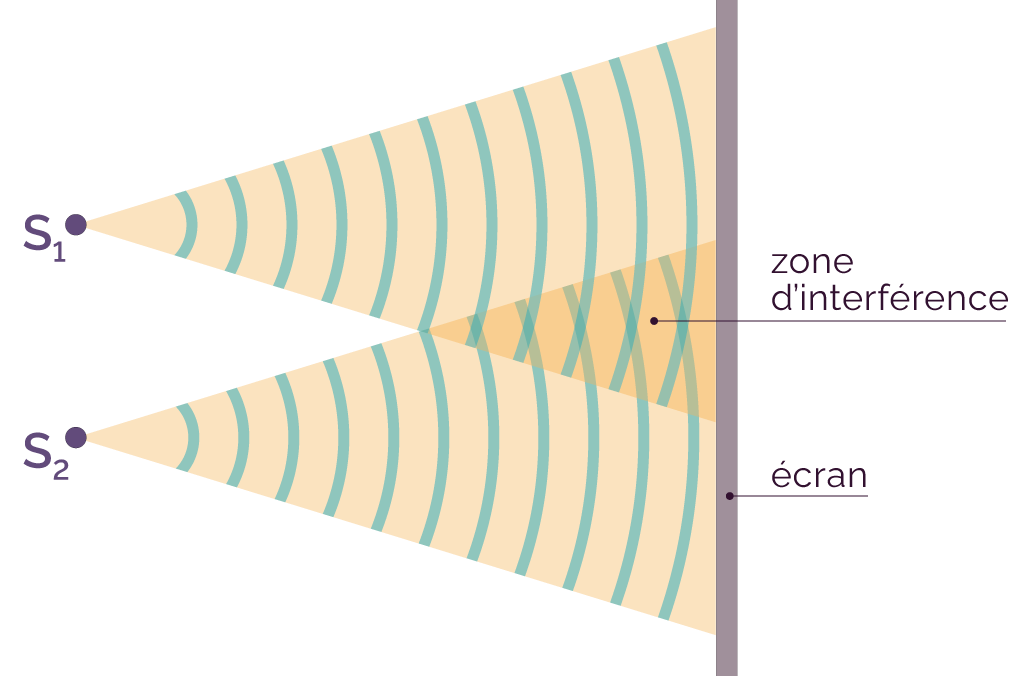
Étude des interférences
avec deux gouttes d’eau
Les deux gouttes se comportent comme deux sources ponctuelles identiques S1 et S2 qui émettent une onde en phase : elles ont le même état vibratoire à tout instant (les ondes passent par un maximum en même temps, etc.).
Lorsque les deux ondes se croisent, le phénomène d’interférences apparait : il résulte de la superposition des amplitudes des ondes produites par les sources S1 et S2.
On positionne trois points sur cette figure d’interférences, puis on étudie l’amplitude de chaque onde et l’amplitude résultante.
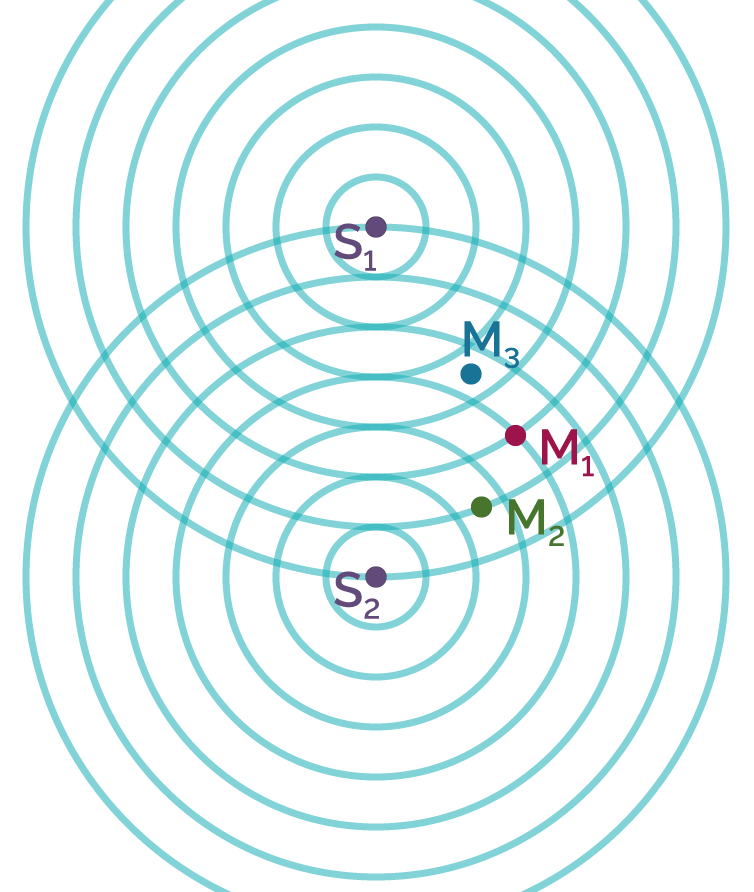
Figure d’interférences vue du dessus
Amplitude résultante de deux ondes en
phase
La sommation des deux ondes en phase conduit à
une onde d’amplitude deux fois plus importante
que celle de chaque onde. On obtient dans ce cas des
interférences constructives.
Les deux sources sont en phase : temporelle (maximales et minimales en même temps) et spatiale (maximales et minimales au même endroit).
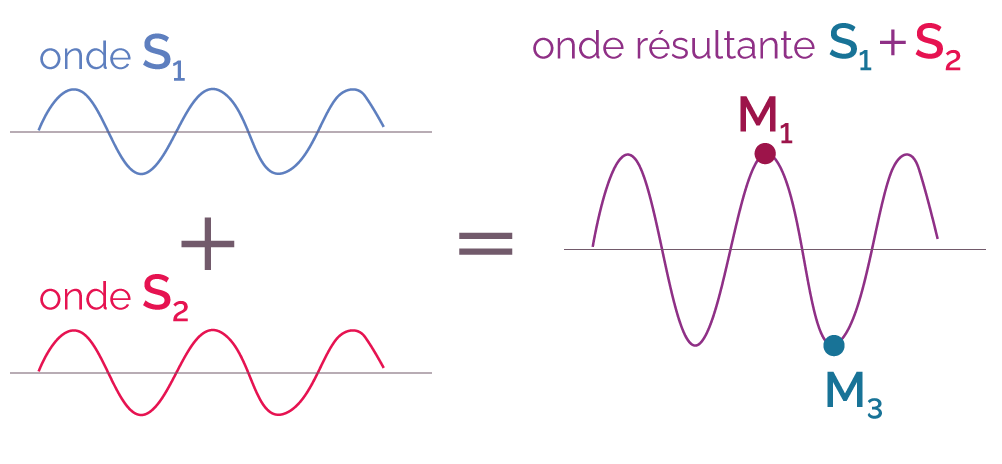
Amplitude résultante de l’onde aux points M1 et M3
Amplitude résultante de deux ondes en
opposition
La sommation des deux ondes en opposition de phase
conduit à une onde d’amplitude nulle. On
obtient dans ce cas des interférences
destructives.
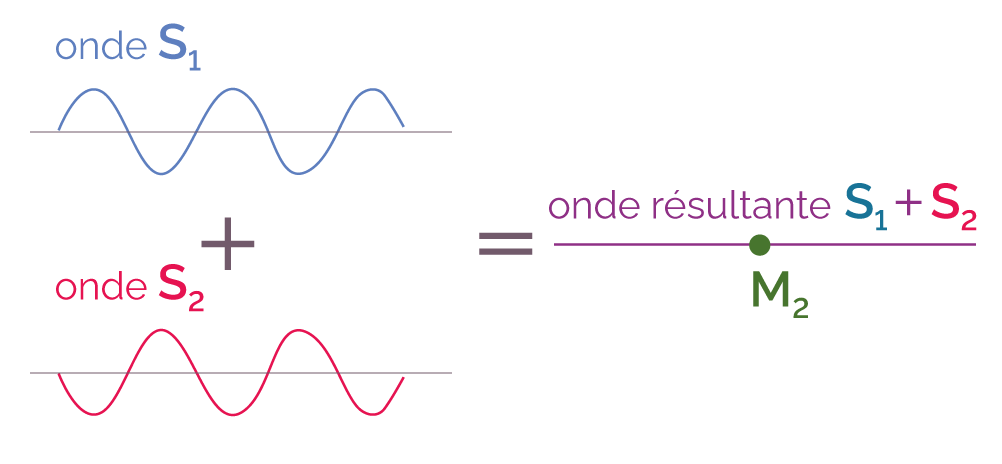
Amplitude résultante de l’onde au point M2
Les deux sources sont en phase temporelle (maximales et minimales en même temps) mais en opposition de phase spatiale (le maximum de l’une coïncide avec le minimum de l’autre et réciproquement).
On s’intéresse à une onde qui rencontre un seul obstacle.
On dispose un trou de diamètre d sur le trajet du faisceau lumineux. On place ensuite un écran après l’obstacle, à une distance D de celui-ci, ce qui permet d’observer la figure suivante sur l’écran.
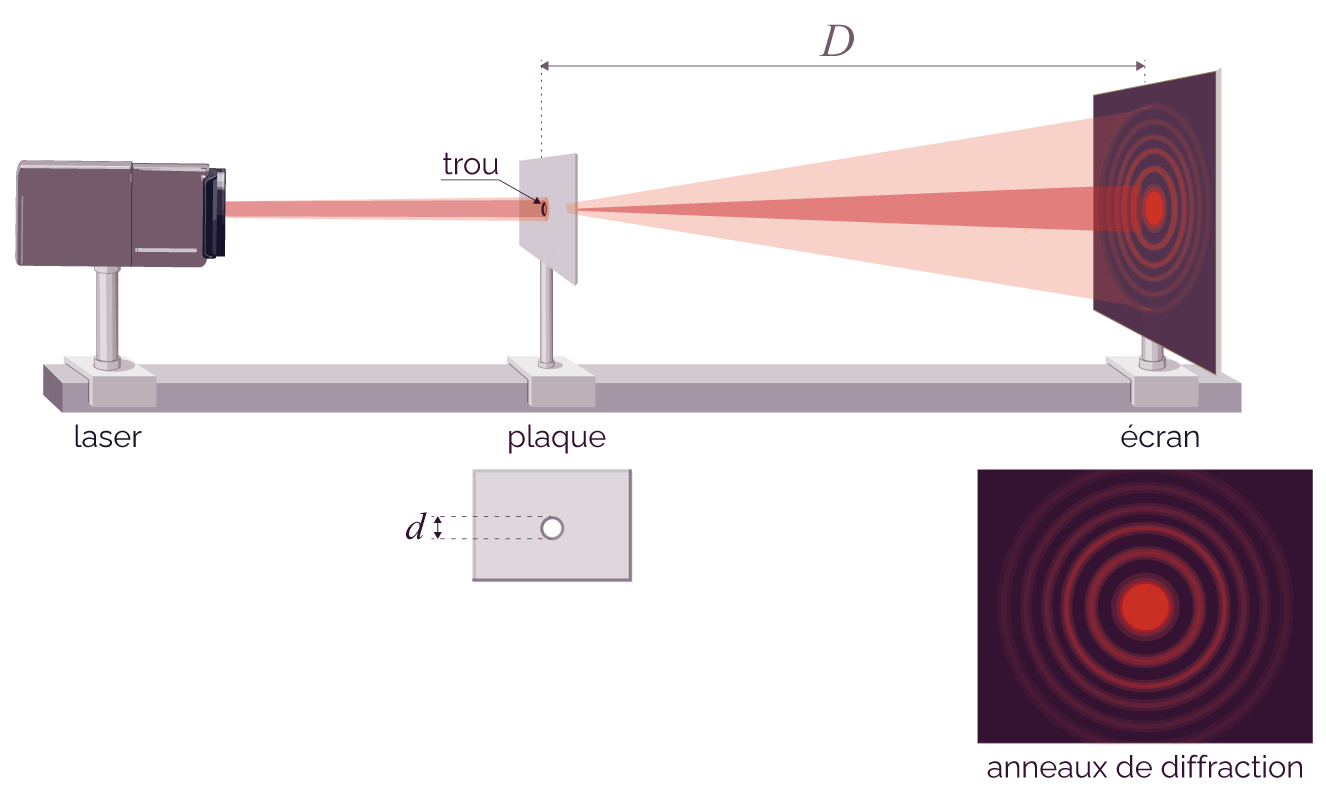
Figure obtenue sur l’écran
On obtient une tache centrale brillante circulaire entourée de tâches circulaires secondaires, régulièrement espacées les unes des autres et séparées par des zones sombres. L’intensité lumineuse des tâches décroit quand on s’éloigne du centre de la figure.
L’onde incidente a été diffractée par l’ouverture circulaire. La figure obtenue sur l’écran est une figure de diffraction. Elle contient le motif de l’obstacle diffractant (ici un cercle).
On s’intéresse au même montage mais cette fois-ci l’onde rencontre deux obstacles.
On perce deux trous circulaires S1 et S2, de diamètre d, dans la plaque opaque. Les trous sont distants d’une longueur a. Le faisceau laser monochromatique de longueur d’onde λ est dirigé normalement au plan de la plaque.
On place un écran derrière la plaque, à une distance D de celle-ci, ce qui permet d’obtenir la figure suivante sur l’écran.
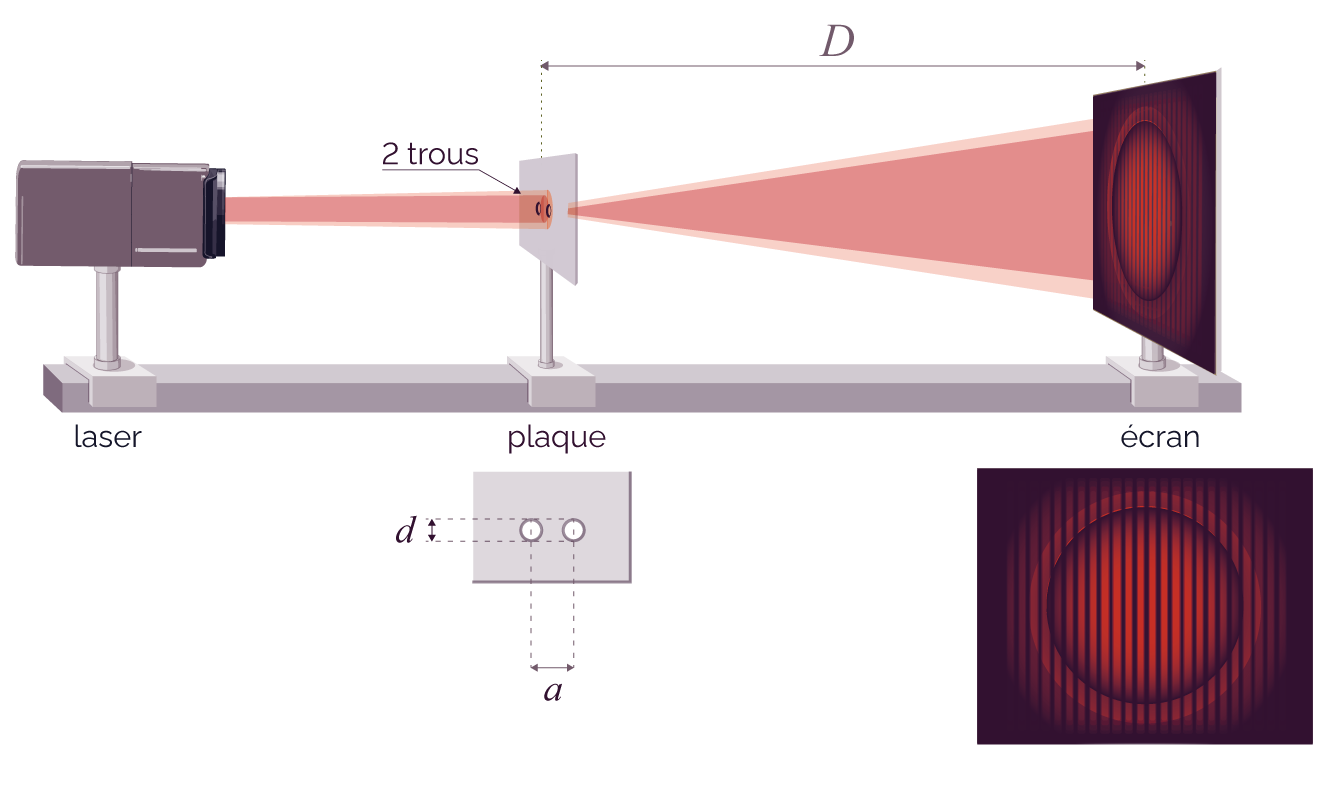
Figure obtenue sur l’écran
On remarque sur l’écran une figure de diffraction, sous la forme d’un disque. Il y a cette fois-ci apparition d’une alternance de lignes sombres et brillantes. La distance entre deux lignes brillantes consécutives est constante.
Cette expérience est nommée « expérience des trous de Young », en référence à Thomas Young (1773–1829) qui découvrit le phénomène en 1803.
L’onde électromagnétique issue de la source se propage jusqu’aux deux trous. Au niveau de chacun d’eux, l’onde qui passe à travers est diffractée. Lorsque les deux ondes se croisent, le phénomène d’interférences apparait.
Cette figure ainsi obtenue résulte de deux phénomènes : la diffraction et les interférences.
La distance entre deux franges brillantes consécutives est constante. Cette distance i est nommée interfrange.
On étudie le schéma suivant pour interpréter le phénomène d’interférences.
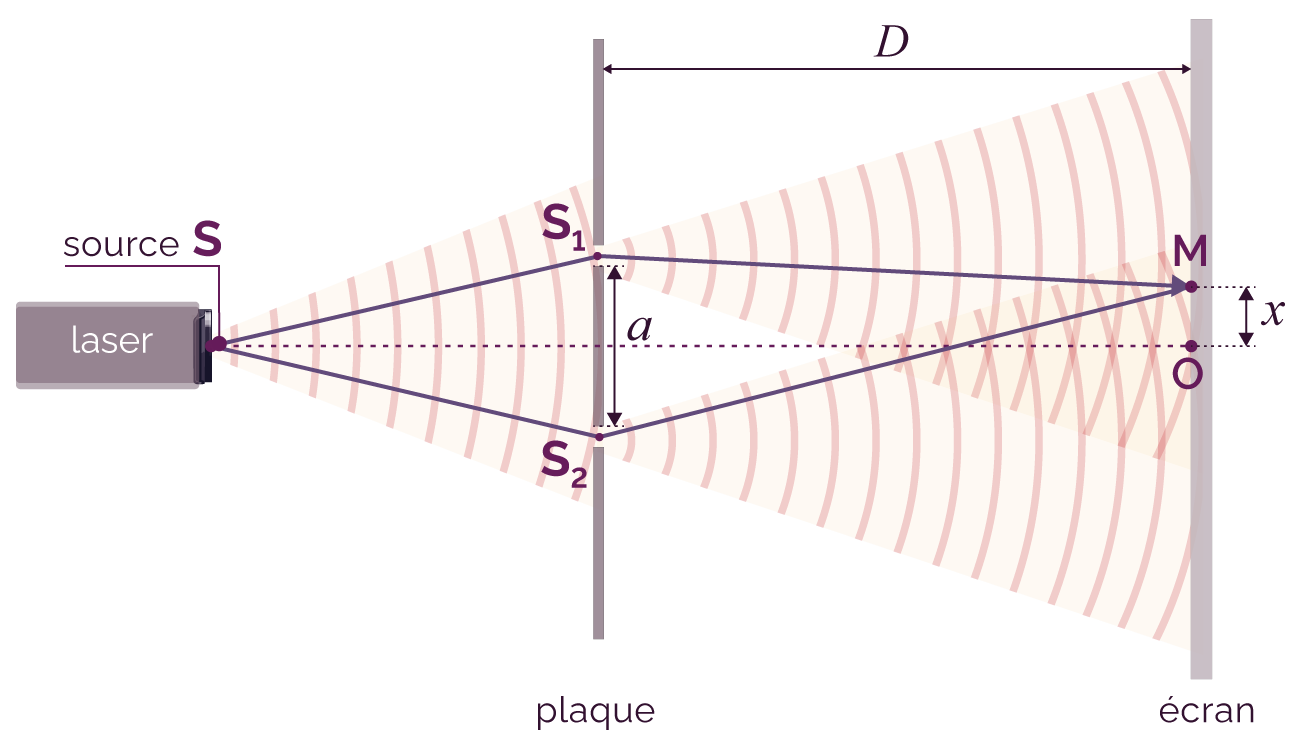
Étude des interférences obtenues avec les trous de Young
Les trous S1 et S2 se comportent comme deux sources secondaires qui émettent une onde ponctuelle identique.
La zone d'interférences correspond à l’endroit où les deux ondes émises par ces deux sources se croisent. La source S étant équidistante des trous, les deux sources secondaires S1 et S2 émettent une onde identique et en phase : elles ont le même état vibratoire à tout instant (amplitude maximale et minimale au même moment, etc.).
On se décale sur l’écran d’une longueur x par rapport au centre de la figure d’interférences O, parallèlement à l’axe (S1S2). On voit que les distances S1M et S2M sont différentes.
En M, les ondes peuvent présenter un déphasage entre elles (leur amplitude n’est pas maximale au même moment mais avec un déphasage).
On positionne trois points sur cette figure d’interférences, puis on étudie l’amplitude de chaque onde secondaire et l’amplitude résultante, selon la valeur de δ.

Figure d’interférences vue du dessus
Amplitude résultante de deux ondes en
phase
Si δ = k × λ,
où k
est un entier relatif (0, ±1, ±2, …),
δ est un
multiple de la longueur d’onde λ. Les ondes sont en
phase.
La sommation des deux ondes en phase conduit à une onde d’amplitude deux fois plus importante que celle de chaque onde.
On a des interférences constructives, comme en O, donc des franges brillantes.

Amplitude résultante de l’onde aux points M1 et M3
Les deux sources sont en phase : temporelle (maximales et minimales en même temps) et spatiale (maximales et minimales au même endroit).
Amplitude résultante de deux ondes en
opposition
Si ![]() , par exemple si δ = 2,5 × λ,
les deux ondes sont en opposition de phase.
, par exemple si δ = 2,5 × λ,
les deux ondes sont en opposition de phase.
La sommation des deux ondes en opposition de phase conduit à une onde d’amplitude nulle.
Les interférences sont destructives. Cela correspond aux franges sombres.

Amplitude résultante de l’onde au point M2
Les deux sources sont en phase temporelle (maximales et minimales en même temps) mais en opposition de phase spatiale (le maximum de l’une coïncide avec le minimum de l’autre et réciproquement).
Lorsque x << D et a << D, la différence de marche s’exprime selon la relation suivante, qu’on admet dans ce cours.
|
|
avec :
|
On cherche à calculer la distance i entre deux franges brillantes.
- Pour une frange brillante,
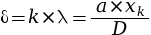 .
.
- En se décalant d’une
longueur i (l’interfrange),
on est sur la frange brillante suivante car la distance
entre deux franges brillantes vaut i.
On a donc :
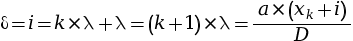
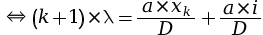
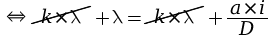
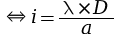
La distance entre deux franges brillantes est ainsi donnée par la relation suivante.
|
|
avec :
|
Pour obtenir des interférences, il faut nécessairement utiliser deux sources. Ces deux sources doivent respecter certaines conditions pour interférer entre elles, auquel cas on obtient juste un brouillage sur l’écran.
- avoir la même fréquence (ou longueur d’onde). On dit alors que les sources sont synchrones ;
- être cohérentes, c'est-à-dire qu’elles doivent avoir à tout instant un déphasage constant entre elles, en un point donné.
- Deux haut-parleurs connectés au même générateur basse fréquence (GBF) peuvent être qualifiés de sources cohérentes (ondes mécaniques).
- Deux sources lumineuses comme deux ampoules sont incohérentes et ne peuvent pas produire d’interférences.
Les trous de Young permettent de fabriquer deux sources identiques et cohérentes en divisant un faisceau lumineux en deux grâce aux deux trous. Il existe aussi l’expérience des fentes de Young qui consiste à remplacer les trous par des fentes.
La figure d’interférences contient le motif de l’obstacle diffractant.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








