Lycée > Terminale > Physique Chimie > Exploiter l'effet Doppler

Exploiter l'effet Doppler

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectifs

Décrire et interpréter qualitativement les observations qui correspondent à une manifestation de l'effet Doppler.
Établir l’expression du décalage Doppler dans le cas d’un observateur fixe, d’un émetteur mobile et dans une configuration à une dimension.
Exploiter l’expression du décalage Doppler dans des situations variées qui utilisent des ondes acoustiques ou des ondes électromagnétiques.
Exploiter l’expression du décalage Doppler en acoustique pour déterminer une vitesse.

Points clés

Lorsqu’une source d’ondes et/ou un récepteur se déplacent, la fréquence captée par le récepteur immobile est différente de la fréquence émise par la source : cela constitue l’effet Doppler.
Le décalage Doppler s’exprime pour une onde par la relation 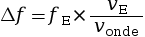, avec :
- Δf = f_R – f_E la différence entre la fréquence f_R reçue par le récepteur et la fréquence f_E émise par l’émetteur, en Hz ;
- v_E la vitesse de l'émetteur, en m·s^–¹ ;
- v_onde la vitesse de l’onde émise par l’émetteur, en m·s^–¹.
L’effet Doppler présente diverses applications car il permet d’estimer à distance la vitesse d’un corps.

Pour bien comprendre

Onde, vitesse, fréquence d'un son
Vitesse d'une onde

1. Les caractéristiques d'une onde qui se propage (rappels)

Une onde (mécanique ou électromagnétique) est caractérisée par sa vitesse de propagation v_onde, sa fréquence f et une double périodicité : temporelle T et spatiale λ.

On s’intéresse à la représentation d’une onde qui se propage dans l’espace.

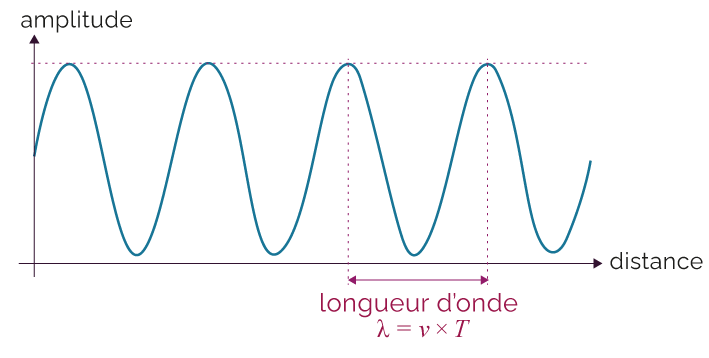
Représentation de l’onde dans l’espace

L’onde possède une périodicité dans l’espace : la longueur d’onde λ.

Celle-ci est reliée à la fréquence f par la relation suivante.

avec :

f la fréquence de l’onde, en Hertz (Hz)
v_onde la vitesse de propagation de l’onde, en mètre par seconde (m·s^–¹)
λ la longueur d’onde de l’onde, en mètre (m)

La fréquence f est donc inversement proportionnelle à la longueur d’onde λ.

2. L'effet Doppler

a. Mise en situation

Les policiers ont mis en route la sirène dans leur voiture de police. On cherche à savoir quel type de son un observateur immobile à l’extérieur de la voiture va percevoir.

Pour cela, on étudie deux cas.

Cas 1 – La voiture est immobile

La voiture est immobile et se trouve à égale distance de deux observateurs A et B. On représente l’onde sonore en jaune.

Représentation de la situation

Observation

L’onde sonore reçue par les deux observateurs a la même longueur d’onde λ et donc la même fréquence f.

Cas 2 – La voiture se déplace

La voiture se déplace en direction de l’observateur B avec une vitesse constante : elle s’approche de B mais s’éloigne de A.

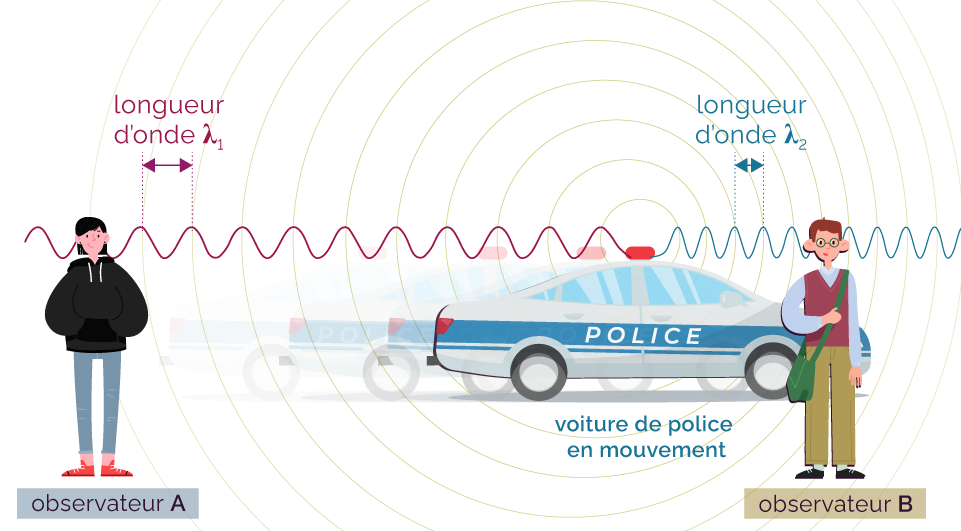
Représentation de la situation

Observation

L’onde sonore reçue par les deux observateurs n’a pas la même longueur d’onde λ et donc pas la même fréquence f : λ₂ < λ₁ donc f₂ > f₁.

Interprétation

Lorsque la sirène se rapproche d’un observateur, celui-ci perçoit un son de fréquence plus petite (et donc plus aigu) que lorsque la sirène s’éloigne.

b. Définition

Lorsqu’un son se déplace par rapport à un observateur immobile, celui-ci perçoit un son de fréquence différente.

Si le son s’approche de l’observateur, le son perçu est plus aigu (la fréquence du son diminue).
Si le son s’éloigne de l’observateur, le son perçu est plus grave (la fréquence du son augmente).

C’est l’effet Doppler : il correspond au changement de fréquence de l’onde perçue par un observateur immobile lors du déplacement de l’émetteur.

3. Décalage Doppler - Cas d'une onde sonore

a. Expression du décalage Doppler

L’expression

On considère un émetteur E qui émet une onde sonore de fréquence f_E (en Hz) et de période T_E (en s). L’onde se déplace à une vitesse v_onde (en m/s).

Le récepteur R, immobile, capte l’onde avec une fréquence f_R, une période T_R et une longueur d’onde λ_R.

La source se déplace avec une vitesse v_E constante et le récepteur est fixe.

Schéma de la situation

Le décalage Doppler correspond à la différence de fréquence entre l’onde reçue f_R et l’onde émise f_E : Δf = f_R – f_E.

L’expression du décalage Doppler est la suivante.

Δf = f_E ×

avec :

Δf = f_R – f_E la différence entre la fréquence reçue par le récepteur et la fréquence émise par l’émetteur, en Hertz (Hz)
f_E la fréquence de l’onde émise par l’émetteur, en Hertz (Hz)
v_E la vitesse de déplacement de l'émetteur, en mètre par seconde (m·s^–¹)
v_onde la vitesse de propagation de l’onde émise par l’émetteur, en mètre par seconde (m·s^–¹) (pour une onde sonore, on a v_onde = 340 m·s^–¹)

Démonstration de l’expression

Voici le calcul par étapes qui permet d’établir cette expression du décalage Doppler Δf.

Cette démonstration n’est pas à connaitre, mais il faut la comprendre.

Étape 1

La source et le récepteur sont distants de D.

À t = 0 s, l’émetteur émet une première onde à la vitesse de propagation v_onde.

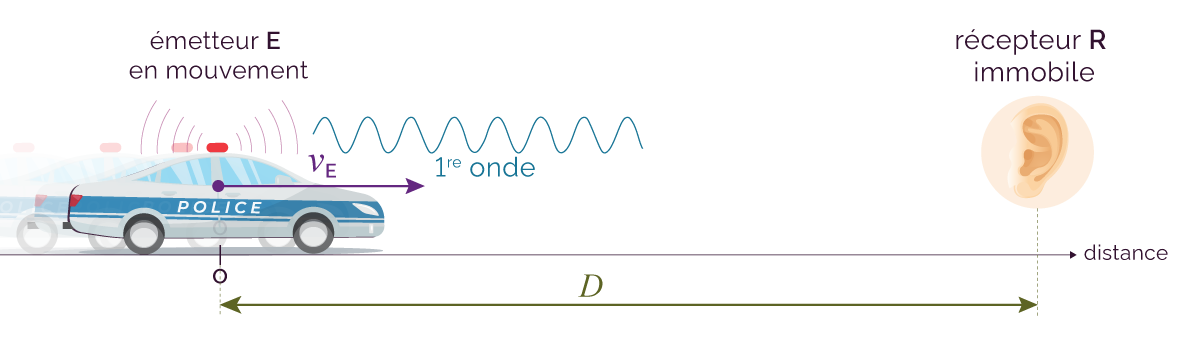
Schéma de la situation à t = 0

Le récepteur recevra cette première onde au bout d’un temps .

Étape 2

Entre temps, la source avance à la vitesse constante v_E et continue d’émettre : une deuxième onde est émise au temps t₂.

La fréquence de l’onde émise par la source est constante et vaut f_E, donc entre deux ondes émises, le temps est constant et vaut .

Pendant ce temps t₂, l’émetteur aura parcouru la distance d₂ = v_E × t₂ soit .

Le schéma correspondant est le suivant.

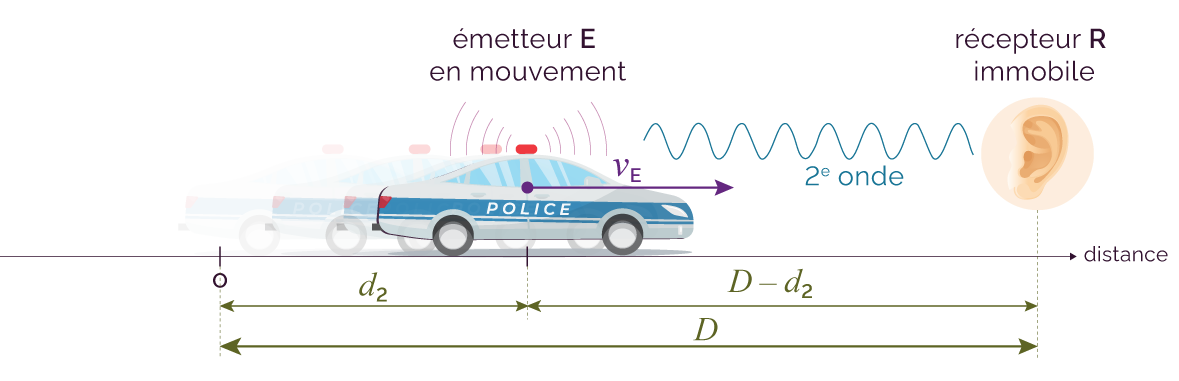
Schéma de la situation à t = t₂

La deuxième onde va parcourir la distance D – d₂ avant d’arriver au récepteur. On a donc D = d₂ + (D – d₂). L’onde se déplace à la vitesse de propagation v_onde donc elle va parcourir la distance D – d₂ en un temps .

La deuxième onde est donc perçue par le récepteur au temps t₃ tel que t₃ = t₂ + .

Étape 3

On peut avoir accès à la fréquence de l’onde reçue f_R en calculant sa période T_R puisque .

T_R correspond au temps entre deux ondes reçues par le récepteur soit T_R = t₃ – t₁ = t₂ + – .

Or et , on obtient donc :

La fréquence f_R vaut donc soit .

La fréquence de l’onde perçue par le récepteur lorsque l’émetteur s’approche à une vitesse v_E est donc .

Le décalage Doppler vaut :
Δf = f_R – f_E

Or on est dans le cas où la voiture se déplace à faible vitesse par rapport à la vitesse du son : v_E << v_onde, on peut donc faire l’approximation v_onde – v_E ≈ v_onde et ainsi obtenir l’expression souhaitée :

Remarque
On peut procéder au même raisonnement pour trouver la fréquence de l’onde perçue par le récepteur lorsque l’émetteur s’éloigne à une vitesse v_E constante.
On trouve

, pour obtenir ensuite le décalage Doppler :

b. Interprétation de l'effet Doppler

On souhaite interpréter la perception de la fréquence sonore perçue par l’observateur immobile lorsque la source approche et lorsque la source s’éloigne.

La source approche

On a vu précédemment que la fréquence de l’onde reçue par le récepteur s’exprime sous la forme .

On sait que v_onde > v_onde – v_E donc et d’où f_R > f_E.

La fréquence perçue par le récepteur f_R est plus grande que la fréquence de l’onde émise f_E : le son est plus aigu.

La source s’éloigne

Si la source s’éloigne du récepteur immobile, on a la formule .

On sait que v_onde < v_onde + v_E donc et d’où f_R < f_E.

La fréquence perçue par le récepteur f_R est plus petite que la fréquence de l’onde émise f_E : le son est plus grave.

c. Application

On cherche à calculer la vitesse d’un hélicoptère qui survole une plaine où se trouve un observateur.

L’onde émise par l’hélicoptère a une fréquence de 7,5 × 10² Hz et l’observateur, immobile, perçoit un son avec une différence de fréquence de 150 Hz.

On utilise la formule soit .

Application numérique : m·s^–1.

L’hélicoptère se déplace donc à une vitesse de 68 m·s^–¹.

4. Décalage Doppler - Cas des ondes électromagnétiques

a. Expression du décalage Doppler

L’effet Doppler concerne également les ondes électromagnétiques, dont les ondes lumineuses. La formule du décalage Doppler est donc la même.

Le principe est le même.

Si l’onde électromagnétique se rapproche de l’observateur immobile, la fréquence perçue par celui-ci augmente.
Si l’onde électromagnétique s’éloigne de l’observateur immobile, la fréquence perçue par celui-ci diminue.

Exemple
On prend le cas d’une étoile.

Lorsque l’étoile se rapproche de la Terre, on observe que son spectre se décale vers les grandes fréquences et donc les petites longueurs d’onde (le bleu pour les raies du visible).
Lorsque l’étoile s’éloigne de la Terre, son spectre se décale vers les petites fréquences et donc les grandes longueurs d’onde (le rouge pour les raies du visible).

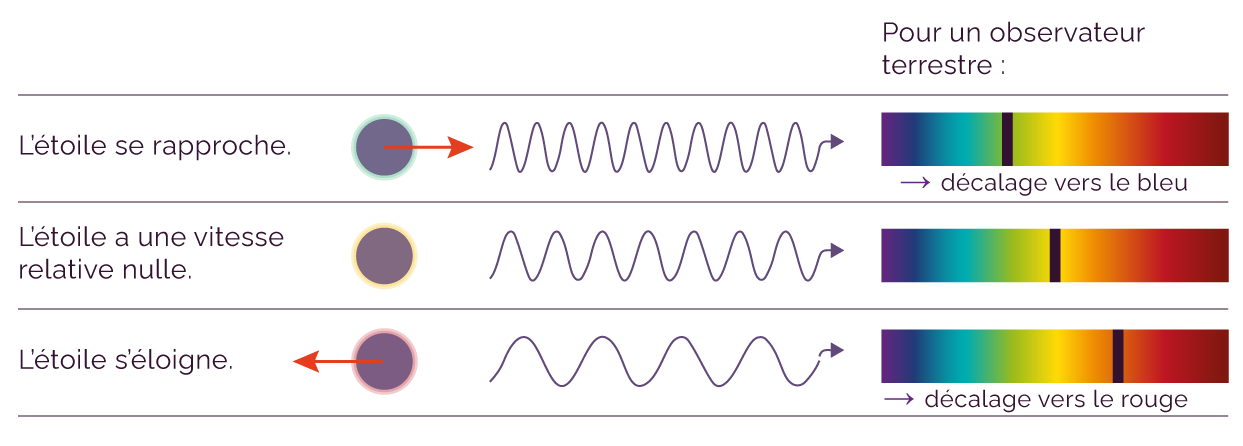
Décalage du spectre d’une étoile selon son déplacement

b. Application - le radar

Le radar automobile est utilisé pour calculer la vitesse de déplacement des voitures sur les routes. On souhaite calculer la vitesse réelle v_réelle d’une voiture.

Le radar émet des ondes électromagnétiques qui se déplacent à la vitesse v_onde = 3,0 × 10⁸ m·s^–¹ et qui ont une fréquence f_E. Le radar constitue un émetteur immobile.

Cette onde est émise en direction de la voiture qui s'approche. Celle-ci roule à la vitesse v_réelle. En raison de sa vitesse, la voiture reçoit l’onde émise par le radar à une fréquence f_R différente de f_E.
Cette onde est ensuite transmise au radar par réflexion mais avec une fréquence différente qui va dépendre de la vitesse de la voiture.
On peut ainsi calculer la vitesse de la voiture.

Il faut tenir compte de l’angle entre la direction du radar et celle de la voiture dans la formule initiale . La vitesse de la voiture v_réelle n’est en effet pas la même que la vitesse v_E mesurée par le radar en raison de cet angle.

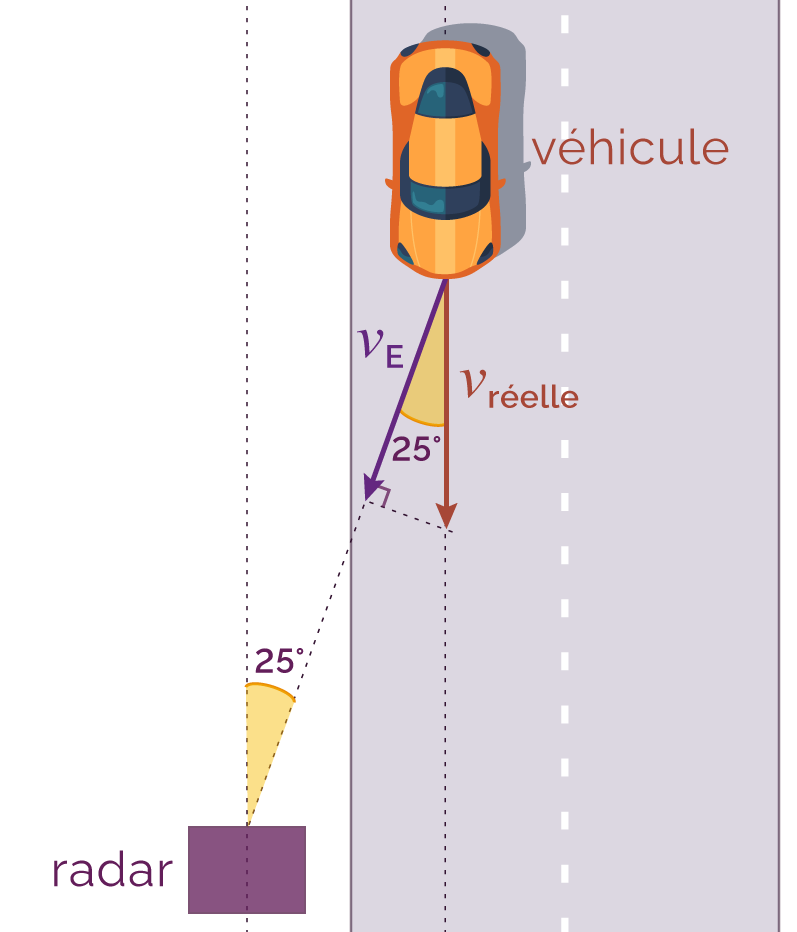
Angle d’inclinaison entre la voiture et le radar

Dans le cas où la direction du radar est inclinée de 25° par rapport à la direction de déplacement de la voiture, la formule du décalage Doppler à prendre en compte est .

Remarque
Cette formule n’est pas à connaitre, elle est toujours fournie.

Exemple
Un radar contrôle un véhicule qui circule en agglomération. Le radar émet une onde de fréquence f_E = 24,125 GHz. Au passage du véhicule la variation de fréquence enregistrée est Δf = 2,5 × 10³ Hz.

On utilise la formule

soit

.

Application numérique :

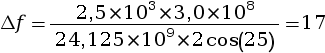m·s^–¹.

Pour savoir s’il est en infraction, il faut convertir cette vitesse en km·h^–¹. On a donc v_réelle = 17 m·s^–¹ = 17 × 3,6 km·h^–¹ = 61 km·h^–¹.

La vitesse en agglomération étant limitée à 50 km·h^–¹, il est donc en infraction.