Éléments de base et instructions conditionnelles

Un algorithme est un plan, un canevas, une liste concise d’opérations à effectuer, une suite d’instructions logiques qui doit permettre d’obtenir le résultat d’un problème que l’on se pose.


► Exemple de problème : Comment calculer la moyenne de trois notes ?

Un algorithme de résolution du problème
Prendre les notes les unes après les autres, les ajouter pour en obtenir la somme totale.
Diviser cette somme totale par trois donne la moyenne.

On peut remarquer qu’il est possible de généraliser cet algorithme pour répondre à la question « moyenne des notes » sans connaître le nombre de notes, avec quelques légères transformations.
Prendre les notes les unes après les autres en les comptant, les ajouter pour en obtenir la somme totale. Diviser cette somme totale par le nombre de notes donne la moyenne.

Il s’agit généralement d’essayer de résoudre un problème de façon automatique (à l’aide d’une machine qui travaille pour nous).

En statistiques, il est agréable d’utiliser une calculatrice ou un tableur pour calculer les caractéristiques d’une liste de donnée : moyenne, médiane, quartiles…
Or, si la moyenne obtenue par la calculatrice est bien celle recherchée, la médiane comme les quantiles (médiane, quartiles, déciles…) ne sont plus calculés avec les mêmes définitions qu’il y a quelques années.
Toutes les calculatrices, tous les tableurs donnent un résultat qui n’est pas celui que l’on doit obtenir avec les définitions actuelles des programmes de mathématiques. L'idée est de construire un petit programme qui donnera « les » bonnes valeurs.

► Le problème des quatre couleurs

C’est grâce à un programme sur ordinateur que l’on a pu démontrer qu’il suffisait de 4 couleurs pour représenter différents pays sur une carte de géographie.
La démonstration a montré que l’on pouvait n’étudier qu’un certain nombre de cas (nombreux), qui ont tous été testés par ordinateur et permis la réponse.

Les différentes variables utilisées seront « affectées » par des valeurs qui pourront être numériques ou alphanumériques (des mots).


On peut écrire « affecter 10 à A » ou plus rapidement on pourra écrire : 10 → A.
Sur calculatrice ou logiciel de programmation, on trouvera : 10 → A, A := 10, A = = 10 ou autres...
Un exemple d’utilisation est donné ci-après.

Remarques générales sur la notation des variables
Par habitude, on utilise :
• I, J, K entiers utilisés comme compteurs (boucles).
• N, M entiers d’utilisations diverses (suites…).
• X, Y, Z réels pour des coordonnées (géométrie) ou en auxiliaires de calcul.

Selon qu’une certaine condition est vérifiée, on fera un certain traitement et si la condition n’est pas réalisée on ne fera rien ou un autre traitement.


► Exemple : Simulation d’un tirage aléatoire « pile-face ».

Les machines possèdent un générateur de nombres aléatoires (on doit dire « pseudo aléatoires »). Il est possible de demander le tirage d’un nombre entre 0 (inclus) et 1 (exclus).
On considère que SI le nombre tiré est inférieur (strictement) à 0,5 on attribue le résultat à la sortie de « Pile », SINON on considère que c’est « Face ».

Remarque
Certains logiciels ou calculatrices permettent d’obtenir le tirage d’un entier compris entre deux bornes (incluses), par exemple entre 0 et 1 (on attribue 0 pour « Pile » et 1 pour « Face »), ce qui est pratique pour simuler un prolongement du problème précédent qui devient la simulation de sortie d’une face d’un dé.

Algorithme

PFACE1	Commentaires
Variables Entrées Traitement Effacer l’écran Afficher « Pile ou Face » PAUSE (jusqu’à l’appui d’une touche) Initialiser aléatoirement X par 0 ou 1 SI X<0,5 ALORS Afficher « PILE » SINON Afficher « FACE » FINSI Sorties Affichages du traitement	Il n’y a pas d’entrée à faire, on peut n’utiliser aucune variable. On aura l’affichage de « Pile » ou « Face » chaque fois que le programme est lancé. On peut ajouter l’instruction « Pause » si elle existe sur la calculatrice pour n’obtenir le résultat qu’après avoir appuyé sur une touche.

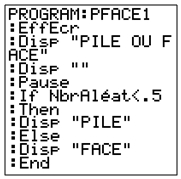
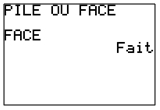
Traduction sur calculatrice (les instructions sont présentées à la suite les unes des autres, alors qu’elles occupent souvent plusieurs écrans).

TI- 84 TI-82 Stat TI-82
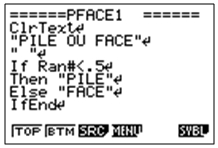
Casio Graph 35+
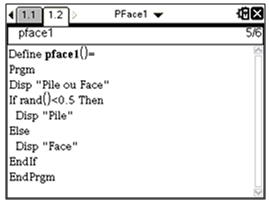
TI-Nspire CAS

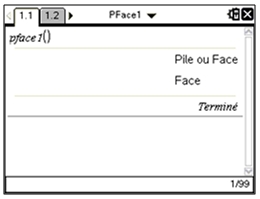
► Exemple du lancer de dé

Le principe
Choisir un nombre entier compris entre 1 et 6, l’indiquer à la machine.
Lancer un dé (utiliser le simulateur de tirage aléatoire).
Si le nombre affiché par la face supérieure correspond au nombre choisi afficher « Gagné », sinon afficher « Perdu ».

Remarque
Certaines calculatrice peuvent donner directement un nombre aléatoire entier compris entre deux entiers (bornes incluses).
Si ce n’est pas le cas, une astuce est de multiplier le nombre aléatoire fourni par la machine (entre 0 inclus et 1 exclus) par la borne supérieure de ce qui est demandé (ici 6), d’en prendre la partie entière (on obtient un entier entre 0 et 5) et d’ajouter 1.

Algorithme

Lancer d’un dé	Commentaires
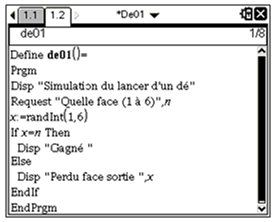
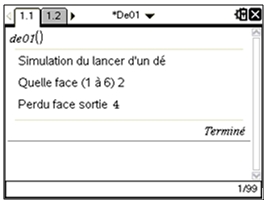
Variables X , N entiers de l’ensemble [1 ; 6] Entrées Lire N Traitement Afficher « LANCER UN DE » Afficher « UN ENTIER DE 1 A 6 » Saisir N Initialiser aléatoirement X par un entier entre 1 et 6 SI X=N ALORS Afficher « Gagné » SINON Afficher « Perdu, face sortie », X FINSI Sorties Affichages du traitement	Les deux variables utilisées sont des entiers de l’intervalle [1 ; 6]. On pourrait se passer de la variable X. Si la calculatrice le fait directement. Sinon il faudra utiliser l’indication ci-dessus.

TI- 84 TI-82 Stat TI-82
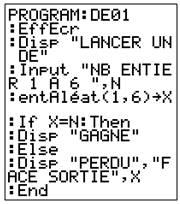
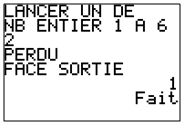
Casio Graph 35+
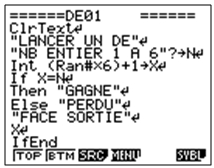
TI-Nspire CAS

Remarque
Ce programme ne vérifie pas que le nombre entré répond aux conditions demandées.
À vous de réaliser ce petit complément avec ce qui a été vu précédemment.