Transitions d'énergie électroniques et vibratoires
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
.Cet aspect est mis en évidence en provoquant des transitions électroniques, absorption et émission, qui ont pour effet de faire passer (au moins) un électron d’un état d’énergie à autre. Expérimentalement, ces transitions sont provoquées par exemple en établissant le spectre d’émission ou d’absorption de l’atome. De part la quantification de l’énergie, on obtient des spectres de raies. Pour le spectre d’émission :
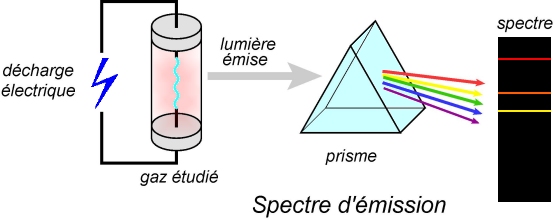
Avec une molécule simple, comme une molécule diatomique, on ne trouve plus un spectre de raies, mais un spectre de bandes. Comment expliquer cela ?
et 
sont reliés par une liaison chimique, assimilable
à un ressort. Comme avec un système
masse-ressort-masse classique, cet ensemble peut
vibrer.
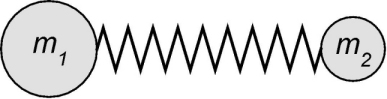
Pour une molécule, il faut cependant utiliser la mécanique quantique pour obtenir une description fidèle aux observations expérimentales. Ce cas d’étude porte d’ailleurs le nom d’oscillateur harmonique. Les énergies de vibration de la molécule sont quantifiées, et satisfont la relation (non exigible) :
est un nombre entier, positif ou nul, servant
à repérer les différents
états vibrationnels. 
où 
est la constante de Planck. 
est une pulsation (en rad/s) où 
est la fréquence associée (en Hz).
Aussi, 
,
avec 
et 
la longueur d’onde correspondante (en m). Comme un
système masse-ressort classique, la
fréquence d’oscillation 
s’écrit :
où
est la masse réduite du système (en
kg) et k la constante de raideur (ou «
constante de force ») de la liaison (en N/m). La
fréquence 
dépend ainsi de la molécule
étudiée. En introduisant le nombre
d’onde 
,
on a :| Molécule |
 en eV
|
 en
|
|
0,541 | 4395 |
|
0,513 | 4138 |
|
0,387 | 3118 |
|
0,371 | 2990 |
|
0,292 | 2359 |
|
0,269 | 2170 |
|
0,196 | 1580 |
|
0,0701 | 565 |
L’ordre de grandeur des énergies observées est de quelques dixièmes d’eV, où
.
Elles sont plus faibles que les énergies
mises en jeu pour les transitions
électroniques. En effet, celles-ci mettent
souvent en jeu des énergies de quelques
eV.
), et de l’énergie vibratoire.
Puisque
,
les états vibrationnels vont en quelque sorte
« s’ajouter » à la structure
créée par les états
électroniques. On parle alors de sous-niveaux
vibratoires.
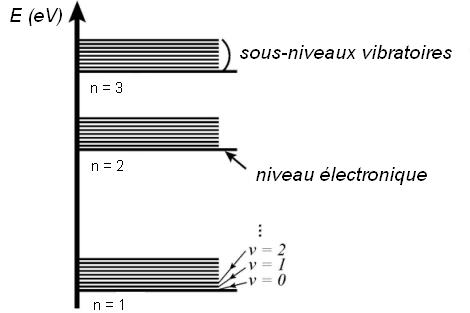
Le diagramme d’énergie permet de deviner que le nombre de transitions possibles va nettement augmenter, tout comme le nombre de longueurs d’onde émises par la molécule lors d’un spectre d’émission. En conséquence, les raies brillantes du spectre atomique se démultiplient en passant au spectre moléculaire, d’où le spectre de bandes observé.
avec j entier positif ou nul
La constante K dépend de la molécule. Les valeurs rencontrées pour les états rotationnels sont encore moins énergétiques que celles des états vibrationnels. En effet, on a par exemple
pour 
,
pour 
,
pour 
,
etc.On écrit donc
,avec
Les états rotationnels vont créer des « sous-sous structures » dans le diagramme énergétique. A moins de disposer d’un appareillage de précision, les états sont trop rapprochés pour être distinguables et semblent donc former un continuum, ce qui explique là aussi le spectre de bandes de la molécule.
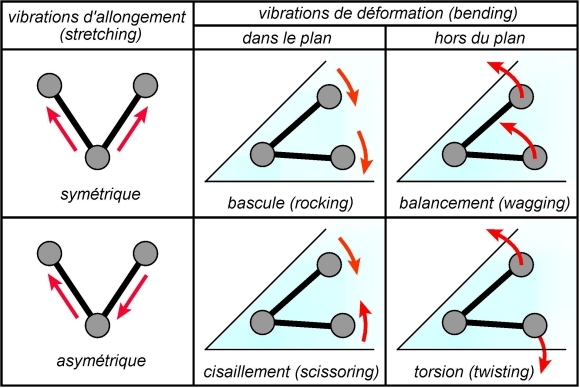
Les vibrations d’allongement (stretching) sont dans l’ensemble plus énergétiques que les vibrations de déformation (bending). Les vibrations de déformation ont des nombres d’onde grosso-modo autour de
alors que les vibrations stretching peuvent monter
au-delà de 
.En spectroscopie, la finalité est de ne provoquer que certains types d’excitations : électroniques, vibrationnelles, mais si possible pas les deux en même temps. Autrement dit, en spectroscopie IR, un rayonnement infrarouge est utilisé pour provoquer des transitions vibrationnelles, associées aux modes de vibrations décrits plus haut. La finalité est de pouvoir reconnaître les transitions et faire alors la correspondance avec les liaisons chimiques concernées, voir fiche sur la spectroscopie IR.
Remarque : comme les énergies rotationnelles sont plus basses que celles des vibrationnelles, des transitions rotationnelles peuvent intervenir dans des spectres IR (phase gazeuse), sous la forme de fines structures.
| Domaine spectral | X | UV-Visible | IR | Ondes radio |
| Type d'excitation |
Transitions électroniques
très énergétiques
|
Transitions électroniques | Vibrationnelles | RMN |
Pour rappel, le visible se situe à des longueurs d’onde comprises en 400 et 800 nm, ce qui correspond à des énergies de 1,55 eV à 3,11 eV. De même, l’UV exploité est entre 100 nm et 400 nm, soit des énergies allant de 3,11 eV à 12,4 eV. En conséquence, les transitions électroniques étudiées concernent des énergies comprises entre 1,5 eV et 12 eV environ. Il existe des transitions électroniques très énergétiques (effet photoélectrique, fluorescence, …), avec des UV plus durs (entre 10 nm et 100 nm) et des rayons X, mais nous n’en parlerons pas.
L’infrarouge va de 800 nm à 1 mm, donc concerne des énergies de 1,24 meV à 1,55 eV. Toutefois, dans la pratique, la spectroscopie IR concerne des longueurs d’onde entre
et 
,
soit des énergies environ entre 0,05 et 0,5
eV.Des spectres purement rotationnels peuvent être obtenus dans le domaine des micro-ondes, de 1 mm à 30 cm, soit des énergies de
à 1,24 meV.
•
: énergies des
électrons de la molécule ; elles sont
quantifiées. Par des transitions quantiques
émission/absorption, des énergies de 1,5 eV
et 12 eV sont mises en jeu : domaine spectral
UV-visible.•
: énergie de la
molécule de part les vibrations au niveau des
liaisons atomiques. Les énergies vibratoires sont
aussi quantifiées. Elles donnent lieu à
des sous-niveaux vibratoires au sein du diagramme
énergétique de la molécule. Les
énergies mises en jeu vont de 1,55 eV à 1,24
meV environ (domaine de l’infrarouge).Les transitions vibratoires sont exploitées en spectroscopie IR.
•
(non exigible) : énergie
rotationnelle de la molécule. Ces
énergies sont également quantifiées et
sont plus faibles que les énergies vibratoires
(micro-ondes).Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Physique Chimie
Dualité onde-particule : photon et onde lumineuse - longueur d'onde de de Broglie
Physique Chimie
Interférences photon par photon / particule par particule
Physique Chimie
Production d'eau potable, traitement des eaux
Physique Chimie
Elaboration, évolution et protection des matériaux
Physique Chimie
Chiralité / carbone asymétrique
Physique Chimie
Conformation et aspect énergétique
Physique Chimie
Isomérie
Physique Chimie
Formule topologique
Physique Chimie
Ondes progressives périodiques / sinusoïdales
Physique Chimie
Ondes sonores et ultrasonores
Fermer
Accédez gratuitement à
