Ondes progressives périodiques / sinusoïdales
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
• Définir une onde progressive mécanique périodique particulière : l’onde sinusoïdale et ses caractéristiques (période, fréquence et longueur d’onde).
Quand la source impose une perturbation périodique, l’onde progressive ainsi générée est elle-même périodique. Cette onde est caractérisée par une double périodicité : temporelle et spatiale.
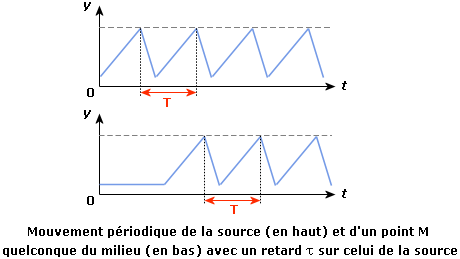
À la source ou en un point donné, on constate que le mouvement observé est périodique. Il est caractérisé par une période T (exprimée en seconde).
Pour un point donné, la période correspond à la plus petite durée non nulle entre deux états vibratoires identiques. Autrement dit, sur le graphe, la période T est par exemple le temps entre deux maximums consécutifs.
La valeur de T n'est pas modifiée lors de la propagation de l'onde. La valeur de cette période caractérise la source.
Au niveau du point M, on constate que le mouvement ne s'instaure pas immédiatement, mais au bout d'un temps τ que l'on appellera le retard. Ainsi, τ est le temps nécessaire pour que l'onde atteigne le point M. Par extension, τ est le temps requis pour que l'état vibratoire produit par la source atteigne le point M (cf. fiche « Ondes progressives à une dimension »).
, où c est la
célérité de l'onde.
, où ƒ s'exprime en Hertz (Hz) et T
en secondes.
Exemples : Quelques fréquences des ondes sonores :
• infrasons : ƒ < 20 Hz
• les sons audibles : 20 Hz < ƒ < 20 000 Hz
• les ultrasons : ƒ > 20 000 Hz
Quand une onde passe d'un milieu à un autre, sa célérité est susceptible de varier (exemple : phénomène de réfraction des ondes lumineuses). Par contre, sa fréquence, et par extension sa période, restent constante durant cette transition.
Autrement dit, c'est comme si on prenait l'onde en photo : on « fige le temps ».
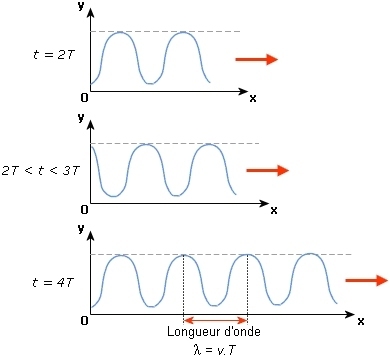
On observe que l’onde possède une périodicité dans l’espace, caractérisée par sa période spatiale, que l'on nomme longueur d'onde, notée λ. Cette grandeur caractérise l'onde. Sa valeur s'exprime en mètres.
Sur un graphe, la longueur d'onde est la plus petite distance non nulle séparant deux points du milieu présentant le même état vibratoire. La longueur d'onde est ainsi par exemple la distance séparant deux maximums consécutifs sur ce graphe.
De manière générale, deux points M et M', séparés d'une distance égale à un multiple de λ ont le même état vibratoire à tout instant : y(x) = y(x + kλ), avec k entier relatif.
Pour une onde deux ou trois dimensions, le raisonnement reste valable, à condition que les deux points appartiennent à deux fronts d'onde différents.
.La longueur d'onde λ est la distance parcourue par l'onde de célérité c en une période temporelle T.
Quand une onde passe d'un milieu à l'autre, nous avons vu que la fréquence et la période restent constantes, alors que la célérité de l'onde est susceptible de varier. En conséquence, d'après cette relation, la longueur d'onde est elle aussi modifiée.
Illustration animée : On dispose d'un chronomètre pour évaluer la célérité de l'onde. On peut définir la période (fréquence) et la longueur d'onde dans le cas d'une excitation sinusoïdale.
Une onde progressive sinusoïdale étant une onde progressive périodique, elle présente donc aussi une double périodicité : temporelle et spatiale. Ainsi, les notions de période et de longueur d’onde sont valables pour les ondes progressives sinusoïdales. D’ailleurs, dans la pratique, les ondes progressives sinusoïdales seront les ondes périodiques les plus utilisées en physique (ce que l’on pourra justifier dans la fiche « analyse spectrale »).
Les sons purs et les ondes lumineuses monochromatiques (une seule fréquence) sont des exemples d’ondes progressives sinusoïdales.
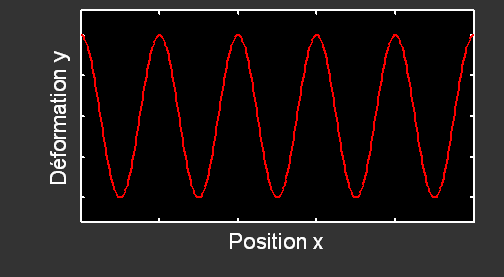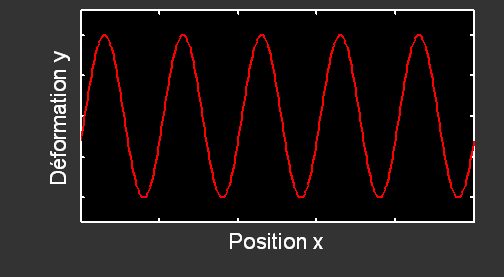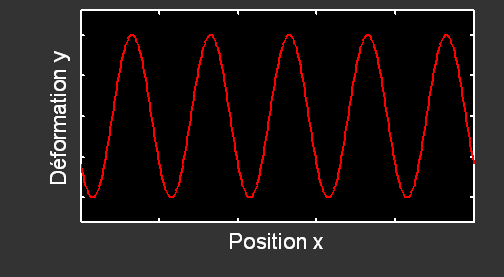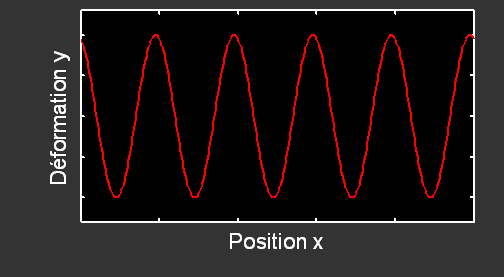
Si l'on étudie l'onde en un point donné, alors on utilise
, où θ est une
phase (en radians), correspondant à un décalage
selon l'axe des temps.Si l'on étudie l'onde pour un temps donné, on a
, où 
(en radians) correspond à
un décalage selon l'axe des x.• Pour un milieu de propagation bidimensionnel, le front d'onde est une ligne.
Par exemple, on peut citer les vagues à la surface de l'eau, que l'on étudie via une cuve à ondes dont le vibreur est relié à un générateur à fréquence variable.
– Si le vibreur est une lame (source étendue), on observe des rides rectilignes : les fronts d'ondes sont des droites. L'onde est dite rectiligne.
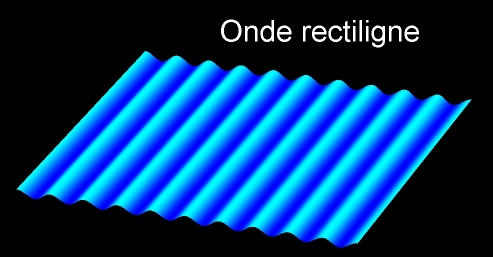
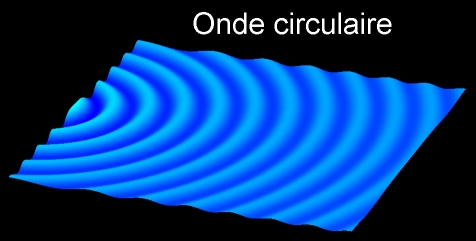
• Pour un milieu tridimensionnel, le front d'onde est une surface. Pour une source ponctuelle, les fronts d'onde dont des sphères concentriques, centrées sur la source, dont les rayons augmentent avec le temps. On dit alors que l'on a une onde sphérique.
Exemples : ondes sonores évoluant dans un milieu de propagation homogène et isotrope.
Une onde progressive périodique présente une double périodicité :
• temporelle, dont la période est notée T et s'exprime en secondes. La fréquence (en Hz) de l'onde est
.• spatiale, avec la longueur d'onde λ, qui s'exprime en mètres, et est reliée à la période T, à la célérité c et à la fréquence ƒ par la relation
.Une onde progressive sinusoïdale est un cas particulier d'onde progressive périodique, qui évolue selon le temps et la distance comme une sinusoïde.
Un front d'onde désigne l'ensemble des points situés à une même distance de la source émettrice de l'onde. Les points situés sur un même front d'onde présentent le même état vibratoire.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Physique Chimie
Ondes sonores et ultrasonores
Physique Chimie
Ondes progressives à une dimension
Physique Chimie
La diffraction
Physique Chimie
Ondes lumineuses : mono/polychromatiques
Physique Chimie
Troisième loi de Newton : le principe des actions réciproques
Physique Chimie
Déterminer la vitesse de réaction et le temps de demi-réaction
Physique Chimie
Principe des techniques d'analyse utilisées en cinétique
Physique Chimie
Mise en évidence des facteurs cinétiques
Physique Chimie
Étude d'un système solide-ressort et des forces de frottements
Physique Chimie
Chaîne de transmission d'informations - signaux analogique et numérique
Fermer
Accédez gratuitement à
