Déterminer la vitesse de réaction et le temps de demi-réaction
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
• Expliquer comment effectuer le suivi de ces réactions, afin de tracer l’évolution de l’avancement en fonction du temps.
• Insister sur les aspects expérimentaux, en indiquant les méthodes possibles de suivi.
• Indiquer comment déterminer le temps de demi-réaction.
Versons dans cette solution un volume V2 = 50 mL d'une solution d'acide oxalique (H2C2O4) de concentration c2 = 60 mmol.L-1
Il se produit alors une réaction d'oxydoréduction entre l'ion dichromate Cr2O72– et l'acide oxalique. Cette réaction met en jeu les couples rédox Cr2O72– / Cr3+ et CO2 / H2C2O4 .
Elle s'écrit :
Cette réaction est lente mais totale, ce qui veut dire d’une part que l’on peut suivre son évolution temporelle, et que, d’autre part, la réaction va évoluer jusqu’à épuisement du ou des réactifs limitants.
n(Cr2O72–) = c1 × V1 = 50,0 × 10–3 × 15,0 × 10–3 = 0,750 mmol.
n(H2C2O4) = c2 × V2 = 50,0 × 10–3 × 60,0 × 10–3 = 3,00 mmol.
La réaction étant totale, l’avancement final xf (réellement atteint par la réaction) est égal à l’avancement maximal xmax (obtenu quand le réactif limitant est épuisé). Le tableau d'avancement de la réaction chimique étudié est donc :
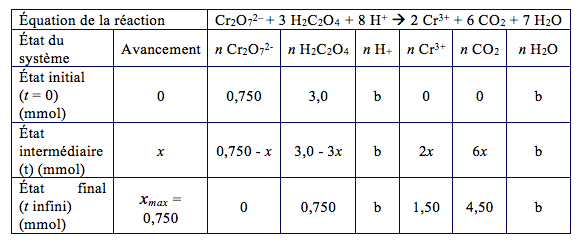
Les ions H+ sont en excès : dans le tableau, on note « b » pour beaucoup : la quantité exacte n'est pas importante.
Même remarque avec l’eau : en tant que solvant, sa quantité de matière est très supérieure à celle des autres espèces chimiques.
→ Si l’ion dichromate est le réactif limitant, alors n(Cr2O72–)i – xmax = 0, d’où xmax = n(Cr2O72–)i ≈ 0,750 × 10–3 mol.
→ Si l’acide oxalique est le réactif limitant, alors n(H2C2O4)i – 3xmax = 0, d’où xmax =
≈ 1,00 × 10–3 mol.Le réactif limitant est celui qui nous donne l’avancement maximal le plus faible. Ici, l’ion dichromate est donc le réactif limitant. On a xmax = 0,750 × 10–3 mol, ce qui nous permet de compléter la dernière ligne du tableau d’avancement.
→ On pourrait penser à suivi par titrage, par exemple de l’ion dichromate, mais une difficulté pratique serait de pouvoir détecter l’équivalence du titrage, ce qui ne serait pas simple ici.
→ La réaction mettant en jeu des ions, un suivi conductimétrique serait possible, mais le lien entre l’avancement x et la conductance G mesurée n’est pas trivial, du fait que la réaction fasse intervenir trois types d’ions.
→ La réaction engendre une production de dioxyde de carbone, sous forme gazeuse. Ainsi, en confinant le milieu réactionnel dans une enceinte étanche et indéformable, on pourrait suivre l’avancement de la réaction en mesurant la pression au sein de l’enceinte : un suivi manométrique serait envisageable.
→ Les ions dichromate sont jaune-orangés, les ions chrome (III) sont verts, les autres espèces intervenant dans la réaction sont incolores. Un suivi spectrophotométrique est donc possible. Les longueurs d’onde d’absorption du l’ion dichromate et de l’ion chrome (III) sont assez différentes pour que l’on puisse mesurer l’absorbance induite par une seule de ces deux espèces chimiques, sans être perturbé par l’autre espèce chimique (en choisissant judicieusement la longueur d’onde du spectrophotomètre). C’est la méthode que nous retiendrons ici.
Avant la manipulation, on mesure l’absorbance de plusieurs solutions étalons de dichromate de potassium de concentrations connues, afin de tracer A en fonction de c. Conformément à la loi de Beer-Lambert, la fonction A(c) est une fonction linéaire dont la pente vaut k. La courbe obtenue est nommée courbe d’étalonnage.
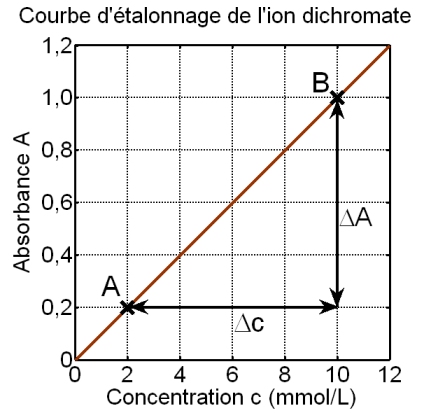
Pour estimer k, on choisit deux points A et B de la courbe, et on écrit k =
≈ 102
L/mol.
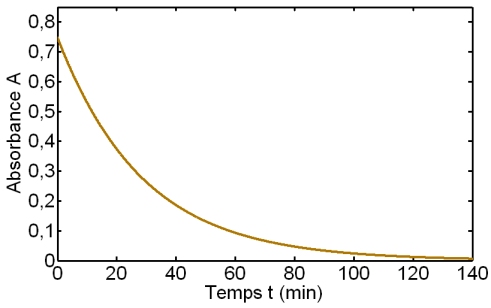
En notant V = V1 + V2 le volume de la solution (considéré comme constant), le tableau d’avancement nous permet d’écrire que
, et donc, nous avons
A = k × c = k × 
. À partir de cette
relation, on obtient 
, soit 
et donc x ≈
10–3 × (0,750 – A),
avec x en mol. Cela nous permet
d’établir le graphe x(t)
à partir de celui de A(t) :
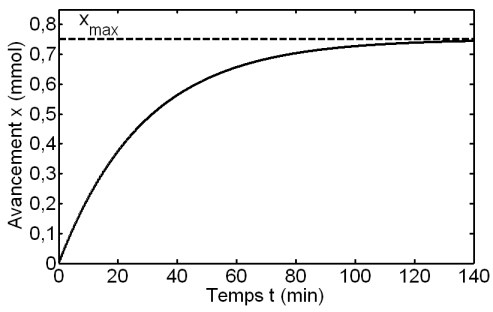
L’avancement x augmente fortement au départ, pour progressivement tendre vers sa valeur limite xmax . D’ailleurs, la valeur de xmax lue sur ce graphe (≈ 0,750 mol) correspond à celle trouvée à l’aide du tableau d’avancement.
, la durée au bout de laquelle
l'avancement x est égal à la
moitié de l'avancement maximal
xmax. Le temps de
demi-réaction s'exprime en secondes (s).
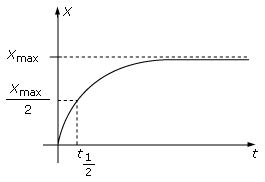
On détermine graphiquement le temps de demi-réaction, qui correspond à la durée nécessaire pour que x =
= 0,375 ×
10–3 mol.
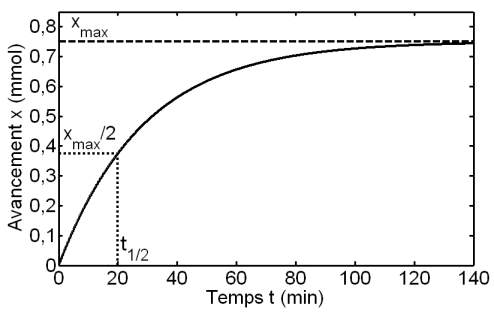
On lit sur le graphique que cette concentration
≈ 20 min.
2 MnO4–(aq) + 5 H2C2O4(aq) + 6 H+(aq) → 10 CO2(aq) + 2 Mn2+(aq) + 8 H2O(l).
Si l’ion permanganate est le réactif limitant, on a :
On peut suivre cette réaction en fonction du temps :
→ Par titrage des ions permanganate par des ions fer (II)
→ Par suivi spectrophotométrie, l’ion permanganate étant de couleur violette ; les autres espèces chimiques intervenant dans la réaction sont incolores.
En choisissant la méthode spectrophotométrique, on mesure ainsi l’absorbance A induite par les ions permanganate en fonction du temps. D’après la loi de Beer-Lambert, A est liée à la concentration c en ions permanganate par la relation A = k × c. La constante k peut être estimée au préalable par une courbe d’étalonnage.
D’après le tableau d’avancement, si le volume de la solution est égal à V (en L), on a c =
et
donc A = k × 
.On en déduit alors la relation donnant l’avancement x (en mol) en fonction de l’absorbance A mesurée :
.À partir de la courbe obtenue, on peut alors trouver le temps de demi-réaction en résolvant graphiquement
.
À partir du graphe de x(t), il est alors possible de déterminer le temps de demi-réaction
de la réaction
étudiée, en résolvant graphiquement
l’équation 
,
c'est-à-dire en déterminant le temps que met
la réaction pour atteindre la moitié de son
avancement maximal.Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Physique Chimie
Principe des techniques d'analyse utilisées en cinétique
Physique Chimie
Mise en évidence des facteurs cinétiques
Physique Chimie
Étude d'un système solide-ressort et des forces de frottements
Physique Chimie
Chaîne de transmission d'informations - signaux analogique et numérique
Physique Chimie
Caractéristiques d'une image numérique
Physique Chimie
Conversion d'un signal analogique en signal numérique
Physique Chimie
Procédés physiques de transmission de données
Physique Chimie
Caractéristiques d'une transmission numérique
Physique Chimie
Stockage optique
Physique Chimie
Conducteurs, semi-conducteurs, supraconducteurs
Fermer
Accédez gratuitement à
