Caractéristiques d'une transmission numérique

Pour une transmission de n bits pendant un temps  (en seconde), le débit binaire D est :

Il est exprimé en bit par seconde, ce qui se note bit/s ou bps. On dispose également des multiples : kilobit par seconde (kbit/s) : , mégabit par seconde (Mbit/s) : , gigabit par seconde (Gbit/s) : , térabit par seconde (Tbit/s) : .

Comme un octet correspond à 8 bits, on exprime aussi un débit en octet par seconde, ou avec ses multiples :
• Multiples en puissances de 10 : kilo-octet par seconde (ko/s), méga-octet par seconde (Mo/s), giga-octet par seconde (Go/s), etc.
• Multiples en puissances de 2 : le kibioctet par seconde (Kio/s), le mébioctet par seconde (Mio/s), le gibioctet par seconde (Gio/s), etc. On rappelle que , , .

Remarque (hors programme) : le baud, de symbole Bd, est une autre unité employée afin d’estimer un débit. Par définition, un baud correspond à un symbole transmis par seconde, où un symbole désigne une lettre, un chiffre, … codé en binaire sous plusieurs bits.

Quelques exemples :
Le débit binaire est spécifique aux signaux numériques. On le rencontre ainsi pour les divers moyens de communications véhiculant ce type de signaux :

→ Pour un câble coaxial, le débit est limité par des phénomènes électromagnétiques. Des débits voisins de 100 mégabit/s sont possibles pour des distances de l’ordre du kilomètre, mais pas au-delà de 10 kilomètres. Le signal est alors trop dégradé.

→ Pour une fibre optique, les débits sont énormes. Les débits standard sont de l’ordre de 100 gigabits par seconde. Des équipes de recherche obtiennent même en laboratoire des débits de quelques térabits par seconde !

Lors de la propagation d’un signal, il s’atténue. Cela se traduit par une baisse de son amplitude. Nous nous focalisons sur des propagations guidées : câbles électrique ou fibres optiques, que nous désignerons sous le terme de ligne, ou de guide de transmission.

On désigne par la puissance du signal avant transmission, lorsqu’il est introduit dans la ligne, et est sa puissance en sortie de ligne. Les puissances sont exprimées en Watt. On a nécessairement , sauf s’il y a un dispositif d’amplification sur la ligne (cas que nous ne considèrerons pas).

peut prendre des valeurs proches, ou au contraire très différentes de , selon plusieurs ordres de grandeurs. Cela justifie l’introduction d’une atténuation A en tant que grandeur logarithmique, selon la relation :

L’atténuation A, aussi nommée affaiblissement, s’exprime en décibel, de symbole dB.

La forme est justifiée par , avec a et b strictement positifs. log est un logarithme décimal (en base 10), voisin mais différent du logarithme népérien ln vu dans le cours de mathématiques.

Propriétés :
→ Si (transmission idéale), .

→ Puisque , d’où ou , c'est-à-dire . L’atténuation est positive ou nulle.

→ Pour donnée, si est divisée par 2, alors A est augmentée de 3 dB.

Démonstration :
soit et . On écrit alors :
car . On a donc .

→ , donc .

Coefficients d’atténuation linéique :
La longueur de la ligne influe sur l’atténuation du signal : pour une ligne donnée, plus la distance parcourue est grande, plus l’atténuation est forte. On peut chercher à caractériser une ligne indépendamment de la distance, afin d’estimer son aptitude à transmettre un signal.

On fait alors appel au coefficient d’atténuation linéique défini comme , où L est la longueur de la ligne, en mètre. Ainsi,

Il s’agit d’une atténuation par unité de longueur, s’exprime en dB/m. Dans la pratique, il est souvent commode d’utiliser des dB/km. Notons que .

Remarque : Dans la littérature, on rencontre aussi un coefficient d’atténuation linéaire a, en , défini comme . Attention à ne pas confondre !

Quelques valeurs :
→ Pour un câble coaxial utilisé pour véhiculer des données à des fréquences de quelques GHz, l’atténuation linéique est voisine de 0,3 dB/m.

→ Dans une fibre optique, est lié à la longueur d’onde de la radiation lumineuse employée. En effet, il existe une interaction entre la lumière et le milieu de propagation (absorption). Les fibres optiques sont faites habituellement en silice. Pour ce matériau, le coefficient d’absorption linéique passe par un minimum lorsque (Infrarouge), où . Ces deux valeurs sont typiques des fibres optiques courantes.

Distorsion
Lors de sa propagation, le signal peut subir des déformations, des distorsions. Il peut y avoir diverses causes à ce phénomène.

Dans le cas des fibres optiques, nous avions vu dans la fiche précédente la dispersion modale. Autrement dit, pour une fibre multimodale, les rayons lumineux se propageant dans la fibre peuvent avoir des trajectoires différentes (plusieurs modes) liés à l’angle initial du rayon par rapport à l’axe de la fibre. Ainsi, ces rayons ne vont pas parcourir la même distance dans la fibre, et vont parvenir à son extrémité en des instants légèrement différents, ce qui entraine cette distorsion.

De manière générale, la distorsion limite le débit. En effet, des informations très rapprochées dans le temps peuvent être « fusionnées » sous l’effet de la distorsion, et seront de fait mal interprétées par le récepteur.


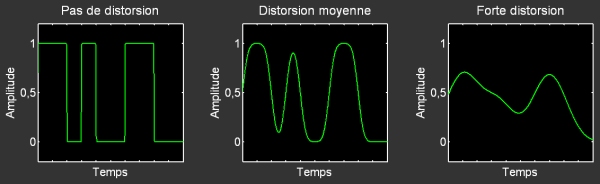
Rapport signal sur bruit (RSB)
L’atténuation correspondant à une baisse de l’amplitude du signal, on pourrait croire qu’un capteur très sensible pourrait quand même extraire les données sans trop de difficultés. Dans la pratique, du bruit se rajoute au signal, ce qui le brouille. Le bruit est constitué de parasites, provenant de divers phénomènes : perturbations électromagnétiques (pour signaux électriques), défauts de la ligne, etc. Par nature, le bruit est de nature aléatoire.

Plus un signal est atténué, plus il se retrouve noyé dans le bruit, et plus il est délicat de l’extraire. On définit le rapport signal sur bruit RSB afin de comparer la puissance du signal à celle du bruit. En anglais, le RSB est nommé SNR ou S/R (Signal to Noise Ratio). Comme pour l’atténuation, on considère une grandeur logarithmique :

où est la puissance du signal, porteuse d’information, et la puissance du bruit, en W. Plus le est fort, plus le signal apparaît nettement. Au contraire, quand le est nul ou même négatif, le signal est dilué dans le bruit.

A gauche, signal peu bruité. Au centre : signal fortement bruité. A droite, signal totalement masqué par le bruit.

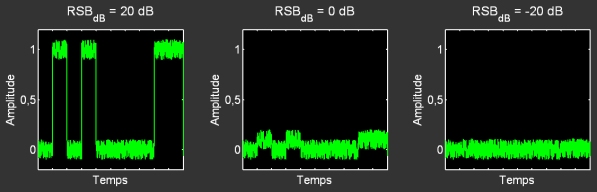
Conséquence d’un signal de mauvaise qualité
L’électronique se chargeant de la réception d’un signal numérique doit être capable d’identifier les 0 et les 1. Si le signal est trop dégradé par la distorsion et/ou le bruit, alors il y a possibilité d’erreurs.

Le taux d’erreur moyen pour une fibre optique utilisée dans des conditions standards est très faible, de l’ordre de 1 erreur pour transmis. Le taux d’erreur est typiquement plus fort pour les câbles électriques, et l’est encore plus pour les communications par ondes.

Par exemple pour la transmission d’un fichier, le récepteur dispose de stratégies pour déceler les erreurs : bit de parité, code CRC (Cyclic Redundancy Check), etc. S’il en détecte une, il peut demander à l’émetteur de ré-envoyer le paquet de données où l’anomalie avait été trouvée.