Fiche de cours

Conversion d'un signal analogique en signal numérique

Lycée > Terminale > Physique Chimie > Conversion d'un signal analogique en signal numérique

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectifs

Décrire la conversion analogique-numérique pouvant intervenir dans une chaîne de transmission de l’information.
Voir ou revoir les notions d’échantillonnage et de résolution d’un convertisseur analogique / numérique (C.A.N.).
Étudier comment convertir des nombres décimaux en nombres binaires, et inversement.

1. Notion d'échantillonnage

Comme nous l’avons vu avec les chaînes de transmission de l’information, un signal analogique varie de manière continue en fonction du temps. Lors de la numérisation d’un tel signal, il y a échantillonnage de celui-ci dans le temps. Cela veut dire que l’on ne mesure les valeurs du signal que périodiquement.

On appelle période d’échantillonnage

(en s) le temps entre deux mesures successives.

La fréquence d’échantillonnage

(en Hz) est son inverse :

La fréquence d’échantillonnage correspond au nombre de mesures effectuées par seconde.

Dans la pratique, elle est réglable pour un échantillonneur donné, mais dans une certaine mesure.

Le choix de la fréquence d’échantillonnage est crucial afin de reproduire fidèlement le signal étudié. En effet, si celui-ci varie trop vite par rapport à

, la numérisation donnera un rendu incorrect du signal. C’est le cas pour le graphe de droite, ci-dessous, où l’échantillonnage donne une sinusoïde avec une fréquence plus faible qu’en réalité. On parle d’aliasing.

Le signal initial est en bleu, les points échantillonnés sont en orange.

Concrètement, le théorème de Nyquist-Shannon indique que la fréquence d’échantillonnage

doit être au moins le double de la fréquence maximale

que comporte le signal :

.

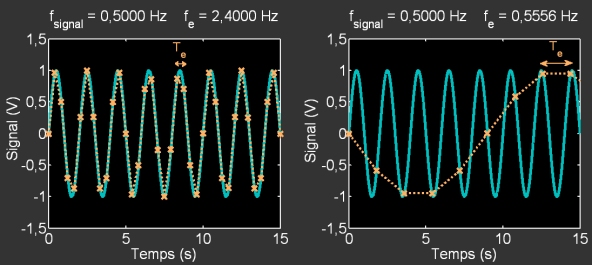
Par exemple, les fichiers audio sont couramment échantillonnés à 44,1 kHz, car cela permet de restituer des sons dont la fréquence peut aller jusqu’à 22,05 kHz, c'est-à-dire un peu au-delà de la fréquence maximale audible par l’Homme (20 kHz).

2. Résolution d'un convertisseur

Un signal numérique ne peut prendre que certaines valeurs : c’est la quantification, assurée par un convertisseur analogique-numérique (C.A.N.). Chaque valeur est arrondie à la valeur permise la plus proche par défaut (juste en dessous).

On appelle résolution l’écart (constant) entre deux valeurs permises successives.

On rencontre aussi le terme de quantum, ou de pas. La résolution q (ou p) d’un convertisseur analogique/numérique de n bits travaillant sur un domaine en tension électrique

est donnée par :

En effet, avec n bits, il est possible de coder

valeurs différentes, donc on divise la longueur du domaine

par le nombre de valeurs possibles. Puisque

s’expriment en Volt, q s’exprime aussi en Volt.

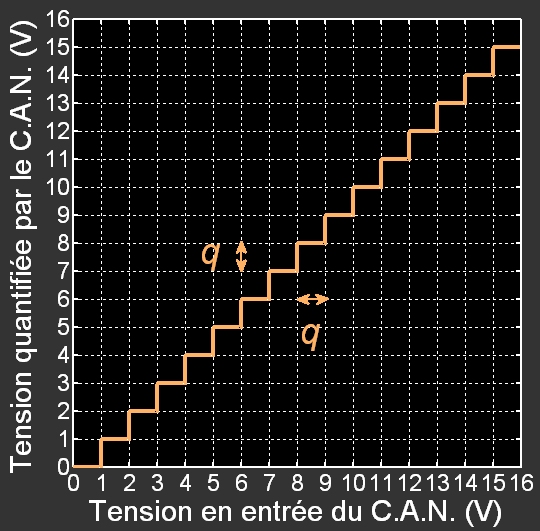
Par exemple, avec un convertisseur 4 bits travaillant entre 0 V et 16 V, la résolution est de 1 V. Le graphe ci-après indique la tension « retenue » par le convertisseur en fonction de la tension d’entrée.

3. Obtention d'un signal numérisé

Schématiquement, l’échantillonnage et la quantification sont réalisés l’un après l’autre, respectivement par un échantillonneur-bloqueur et par le C.A.N. Concrètement, on a les étapes suivantes :
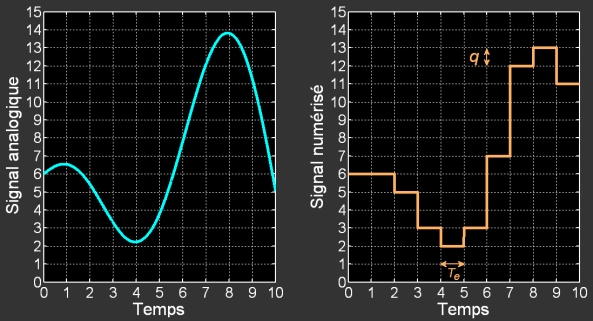
• A des intervalles de temps régulier

, l’échantillonneur-bloqueur mesure la valeur de la tension délivrée par le signal.
• Jusqu’à la prochaine mesure, il maintient la dernière valeur trouvée. Cela justifie le terme de bloqueur : la valeur en sortie reste constante pendant une période d’échantillonnage .
• La valeur est transmise au C.A.N. qui procède à la quantification, selon la valeur de sa résolution q.

En sortie, on obtient le signal numérisé que l’on a observé dans la fiche liée aux chaines de transmission.

4. Le codage en binaire

Dans la pratique, le signal numérisé tel que représenté au 3 n’est pas transmis en l’état. Il est en effet codé en binaire. Cela constitue la dernière étape de la conversion analogique-numérique. Comme vu dans une fiche précédente, le binaire travaille uniquement avec deux chiffres : 0 et 1. Un nombre binaire est un groupement de chiffres binaires (bits).

Exemple : considérons un convertisseur 4 bits travaillant entre -4V et +4V, donc la résolution est

. 4 bits signifient que l’on peut coder

valeurs différentes. Concrètement, le convertisseur travaille donc avec 16 niveaux de tension différents. A chaque niveau correspond un nombre binaire de 4 bits. Exemple, le niveau 0 Volt est associé au binaire 1000.

Remarque : Le signal analogique ne devrait pas valoir 4 V, sinon il faudrait avoir le binaire 10 000 (=16) en sortie, ce qui n’est pas possible pour un C.A.N. 4 bits, car 10 000 fait 5 bits (5 chiffres). Cela justifie l’écriture

, où l'on exclut

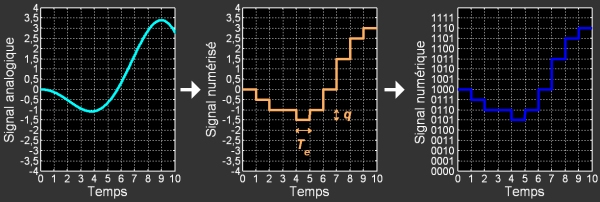
Il est intéressant de remarquer que le lien entre un niveau de tension et le nombre binaire associé n’est pas nécessairement une relation de proportionnalité. On est bien dans l’esprit d’un codage : si le destinataire ne sait pas comment les données binaires ont été codées, il ne pourra pas reconstituer le signal de départ.

Dans la pratique, les données binaires sont véhiculées de deux manières :
• On affecte un fil par bit. Ce genre d’architecture se rencontre en électronique et en informatique : notion de bus parallèle ou de nappe de fils.
• Pour les transmissions entre machines ou autres (liaisons séries dont USB, réseau, fibre optique), on préfère minimiser le nombre de fils. Les bits sont transmis les uns après les autres sur un seul fil. Cela nécessite un protocole de communication adapté entre les appareils connectés.

5. Conversions décimal/binaire : techniques de calcul (non exigible)

Dans cette partie, étudions comment convertir « à la main » un nombre entier positif exprimé dans le système décimal (base 10) en un nombre binaire (base 2), et inversement. Bien entendu, ce genre de calcul peut être effectué par outil informatique (fonction calculatrice de l’ordinateur) ou avec une calculatrice graphique programmable. Un nombre décimal sera noté

et un nombre binaire

a. Conversion décimal --> binaire

Pour convertir un entier positif en base 10 en un nombre binaire, on divise le nombre décimal par 2. On note son reste entier. Puis, on divise le quotient obtenu par 2. On note son reste, et ainsi de suite... jusqu’à obtenir un quotient égal à 0 ou 1. On lit alors le nombre binaire, comme indiqué par le schéma :

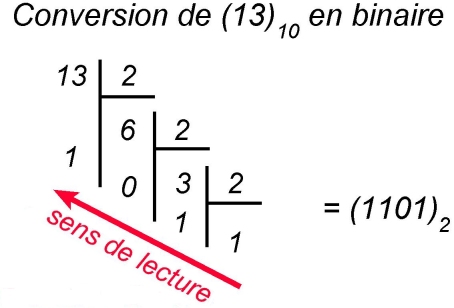
Remarque (hors programme) :
• Il est de même possible de convertir un nombre entier relatif de la base 10 vers la base 2, et inversement. On parle alors de nombre signé.
• Il existe également des conventions de codages pour convertir un nombre réel base 10 en binaire, notamment selon la norme IEEE-754. La structure du nombre codé est proche de la notation scientifique que l’on connaît (mantisse, exposant). Bien entendu, le codage d’un nombre réel passe par un arrondi de celui-ci.

b. Conversion binaire --> décimal

Pour convertir un nombre binaire en un nombre entier base 10, on procède comme indiqué par le schéma ci-après. Le poids d’un bit désigne son emplacement dans le nombre binaire. Le bit le plus à droite a le poids le plus faible, c'est-à-dire 0. Il est équivalent aux unités en base 10. Le bit le plus à gauche a le poids le plus fort.

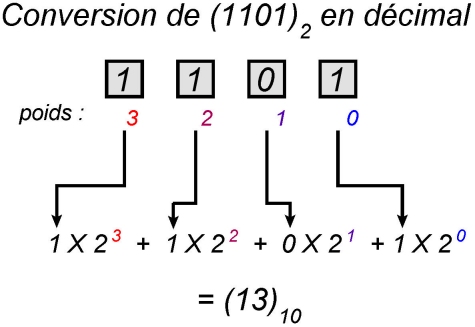
Pour chaque poids i, on multiplie la valeur du bit correspondant (0 ou 1) par

. Ensuite, la sommation des nombres trouvés nous donne le nombre base 10 voulu.

L'essentiel

La conversion d’un signal analogique en signal numérique correspond à 3 étapes :

• Echantillonnage : la valeur du signal n’est mesurée que périodiquement. Le temps entre deux mesures consécutives est la période d’échantillonnage

, son inverse est la fréquence d’échantillonnage

. Celle-ci doit être au moins deux fois plus grande que la fréquence la plus forte

composant le signal, selon le théorème de Nyquist-Shannon.

• Quantification : les valeurs mesurées sont arrondies, afin que le signal numérisé ne prenne qu’un nombre fini de valeurs différentes. Pour un convertisseur analogique-numérique (C.A.N.) n bits travaillant sur un domaine en tension

, la résolution q du convertisseur est

. C’est l’écart entre deux valeurs permises consécutives.

• Codage. Pour sa transmission, le signal numérisé est codé en binaire, c'est-à-dire en base 2. Un nombre binaire est composé de chiffres binaires, les bits (0 ou 1).

Évalue ce cours !

Note 4.1 / 5. Nombre de vote(s) : 176

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT