Interférences photon par photon / particule par particule

Dans l’expérience des fentes de Young, une radiation monochromatique (un faisceau LASER dans une version moderne) est envoyée sur une plaque percée de deux fentes fines, proches l’une de l’autre.


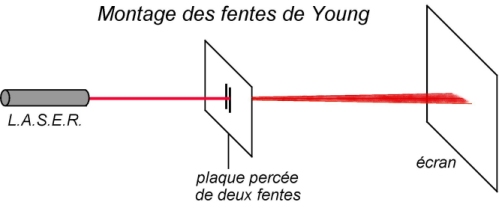
Avec une seule fente, on aurait obtenu un motif de diffraction, caractérisé par un élargissement du faisceau lumineux émergent de la fente, et la présence de structures moins lumineuses de part et d’autre du lobe central. Avec deux fentes, comme avec les trous de Young (voir fiche interférences), il apparaît une alternance de franges brillantes et sombres typique du phénomène d’interférences.



On se focalise sur la zone centrale du lobe le plus lumineux, délimitée par le carré blanc sur la figure de gauche. Dans cette zone, on note la structure régulière des franges d’interférences.

Dans la fiche « dualité onde/particule », il a été vu que la lumière possède un double comportement onde/particule. Les interférences vues au 1. sont l’illustration du comportement ondulatoire de la lumière.
→ Mais qu’en est-il pour les photons, dans le cadre du modèle corpusculaire ?
→ Comment « choisissent-ils » leur trajectoire jusqu’à l’écran : se « mettent-ils d’accord entre eux » par une interaction photon/photon ?
→ Comment les photons permettent-ils d’obtenir la figure d’interférences du 1. ?

Pour tenter de répondre à ces questions, on considère une source lumineuse monochromatique de très faible puissance. Son débit en photons est tel que l’on peut considérer qu’ils sont émis un par un. Au lieu de l’écran, on dispose par exemple un capteur CCD ultrasensible, qui détectera chaque impact de photon, ainsi que la position de celui-ci.

La figure ci-dessous montre les résultats obtenus en fonction du nombre N de photons captés. Chaque point blanc correspond à un photon. Au début, les photons semblent se répartir de manière aléatoire, puis dessinent peu à peu les franges brillantes et sombres.


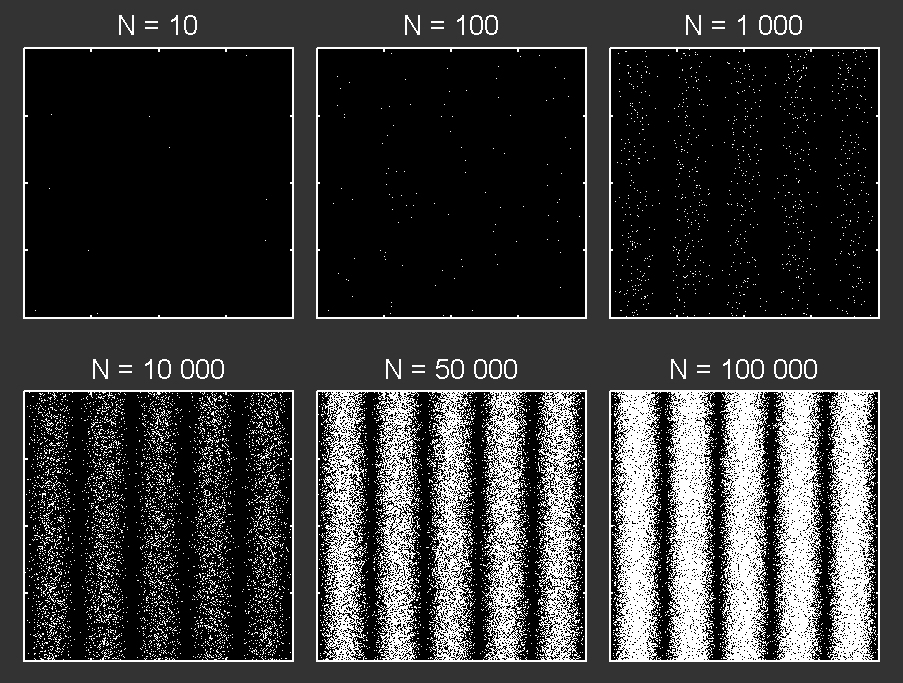
Dans l’expérience, les photons sont émis un par un, ils ne peuvent donc pas « s’influencer mutuellement ». D’ailleurs, de manière générale, les photons n’interagissent pas entre eux. Chaque photon agit indépendamment des autres.

D’autre part, on note un aspect probabiliste : les photons se répartissent au hasard, mais selon une loi de probabilité identique pour chacun, qui fait qu’il y a apparition de zones probables (les raies brillantes) et de zones moins probables (les raies sombres). La figure d’interférences du 1. résulte finalement de l’action d’un grand nombre de photons.

D’un point de vue prédictif, on peut estimer que le photon a de fortes chances de percuter le détecteur au niveau d’une frange brillante, mais on ne sait pas par quelle fente il passe (peut être même les deux à la fois …). Si maintenant on ferme une des deux fentes, on sait alors forcément par laquelle il va passer. Mais dans ce cas là les interférences disparaissent, et seule la diffraction subsiste. Les points d’impact se répartissent alors de manière quasi uniforme. Ainsi, pour prédire le comportement du photon, on gagne d’un côté, mais on perd de l’autre, de sorte qu’il subsiste toujours une incertitude.

C’est une manifestation du fait que la théorie quantique, qui décrit le comportement du photon, est une théorie probabiliste. Il n’est jamais possible de prédire complètement le comportement d’un objet quantique. Ce n’est pas que la théorie n’est pas complète, comme le pensait Einstein (« Dieu ne joue pas aux dés »), mais qu’un objet quantique a intrinsèquement un comportement probabiliste. Certes il est possible de déterminer une loi moyenne (la figure d’interférences dans notre expérience), mais pas le comportement individuel de chaque photon.

Dans la fiche « dualité onde/particule », ladite dualité a été étendue aux objets quantiques de masse non nulle. En effet, Louis de Broglie explique en 1923 que le caractère ondulatoire d’un objet quantique de masse m et de vitesse v est donnée par la longueur d’onde (de de Broglie) , avec h la constante de Planck, et sa quantité de mouvement (). Comment cela peut-il se traduire concrètement ?

Un premier élément de réponse fut donné en 1927 par Davisson et Germer, en mettant en évidence la diffraction d’électrons sur un cristal de nickel, comme le feraient des rayons X. Cette manipulation donna une confirmation expérimentale de l’hypothèse de de Broglie.

Après, on peut reprendre l’expérience du 2. en « remplaçant » les photons par des électrons. Cela demande de remplacer la source lumineuse par un canon à électrons, qui les émettra un par un, à une vitesse constante. D’autre part, le capteur de photons est remplacé par un détecteur à électrons. L’expérience devra être réalisée dans le vide, comme dans les tubes cathodiques.


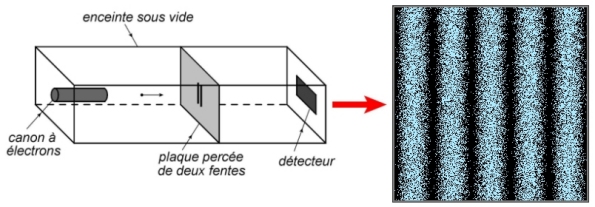
Si la longueur d’onde de de Broglie des électrons est égale à celle qu’avait les photons, on observe exactement le même résultat qu’au 2. En conclusion, les électrons subissent le phénomène d’interférences, comme les photons. Le caractère probabiliste s’applique également aux électrons, comme à tout objet quantique, car ils viennent également frapper le détecteur de manière aléatoire, mais en dessinant aussi peu à peu les franges sombres et brillantes. Comme au 2., on a accès dans l’expérience à la position de l’électron quand il frappe le détecteur. Par contre, on ne sait pas non plus par quelle fente il est passé (les deux en même temps peut-être aussi …).

Remarque : si la longueur d’onde de de Broglie des électrons est largement inférieure à la largeur des fentes et à leur écartement, il n’y a pas diffraction et interférences. Les électrons se comportent alors comme de petites billes, qui viennent dessiner l’image géométrique des deux fentes sur la face du détecteur.

Les microscopes optiques utilisent des lentilles pour obtenir une image agrandie d’objets microscopiques : cellule, bactérie, etc. Même avec les meilleurs microscopes, le grossissement est limité (2000 au maximum). La longueur d’onde de la lumière visible est de 400 nm à 800 nm. Lorsque les objets observés ont des dimensions comparables ou inférieures à ces longueurs d’onde, la diffraction de la lumière induit fatalement une image floue, d’où une limitation de l’instrument. Le pouvoir de résolution d’un microscope, c'est-à-dire sa capacité à donner deux images séparables de deux points distincts, descend difficilement en dessous de la fraction de micromètre. La limite théorique est estimée à pour les microscopes optiques classiques.

Pour observer des objets plus petits, une solution est de « remplacer » les photons visibles par des objets quantiques de longueurs d’onde plus petites. Cela peut se faire avec des électrons. Selon la relation (avec ), leur longueur d’onde de de Broglie est liée à leur vitesse v, que l’on sait modifier (canons à électrons) en conséquence.

Cela constitue le principe de fonctionnement du microscope électronique. Comme expliqué au 3., il est nécessaire de travailler sous vide et d’adapter la technologie employée. Les lentilles optiques sont remplacées par des lentilles magnétiques, afin de dévier la trajectoire des électrons. Il existe deux variantes de microscope électronique :

• Les microscopes électroniques par transmission (MET), mis au point en 1931. Dans cette variante, les électrons traversent les échantillons à analyser. Ces derniers doivent être peu épais (inférieur à quelques centaines de nm). Les images 2D produites sont utilisées par exemple en biologie : images de virus, bactéries, … La résolution de cet appareil peut descendre jusqu’à 0,1 nm environ.

• Les microscopes électroniques à balayage (MEB), apparus dans les années 60. Le principe est également d’envoyer un faisceau d’électrons sur l’échantillon. Cela provoque alors trois phénomènes : rebond de ces électrons (électrons rétrodiffusés), arrachages d’électrons à des atomes de l’échantillon (électrons secondaires), et émissions de rayons X ou d’électrons (effet Auger) par les atomes ainsi ionisés. Les électrons et rayons X sont captés et analysés. Par un balayage du faisceau d’électrons, l’appareil reconstitue alors une image de la surface de l’échantillon, avec un rendu 3D. Les MEB sont utilisés dans des domaines comme la physique des matériaux ou la biologie. Leur résolution peut atteindre environ 0,5 nm