Lycée > Premiere > Sciences > Le son, phénomène vibratoire

Le son, phénomène vibratoire

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectifs

Exploiter le spectre d’un son.
Identifier des sons purs et composés.
Relier puissance sonore par unité de surface et niveau d’intensité sonore exprimé en décibels.
Relier qualitativement la fréquence fondamentale du signal émis et la longueur d’une corde vibrante.

Points clés

Un son pur est associé à un signal dépendant du temps de façon sinusoïdale.
Un signal périodique de fréquence f se décompose en une somme de signaux sinusoïdaux de fréquences multiples de f. Le son associé à ce signal est un son composé. f est appelée fréquence fondamentale, les autres fréquences sont appelées harmoniques.
La puissance par unité de surface transportée par une onde sonore est quantifiée par son intensité. Son niveau d’intensité sonore est exprimé en décibels selon une échelle logarithmique.
Une corde tendue émet en vibrant un son composé dont la fréquence fondamentale ne dépend que de ses caractéristiques (longueur, tension, masse linéique). Dans les instruments à vent, un phénomène analogue se produit par vibration de l’air dans un tuyau.

Pour bien comprendre

Notions de son et de fréquence

1. La production et l'analyse d'un son

Les instruments de musique produisent des sons harmonieux à l’oreille. Le son est une vibration qui se propage de proche en proche dans l’air, de l’émetteur (l’instrument) au récepteur (le tympan). Il est possible de visualiser les sons produits par les instruments et d’en faire l’analyse.

On distingue deux types de sons : les sons purs et les sons composés.

a. Les sons purs, l'exemple du diapason

Le diapason est un instrument produisant une seule note. Le son produit est utilisé comme note de référence pour accorder tous les instruments. Cette note est le la 440.

Visualisation du son produit par un diapason

Afin de visualiser le son produit, on utilise un microphone relié à un boitier d’acquisition des données.

D’abord, le microphone transforme le signal sonore émis par le diapason en un signal électrique. Ce signal électrique est transmis au boitier d’acquisition.

Ensuite, le boitier d’acquisition transforme le signal électrique en un signal numérique. Le signal numérique est traité par un logiciel qui permet de visualiser l’amplitude du son en fonction du temps.

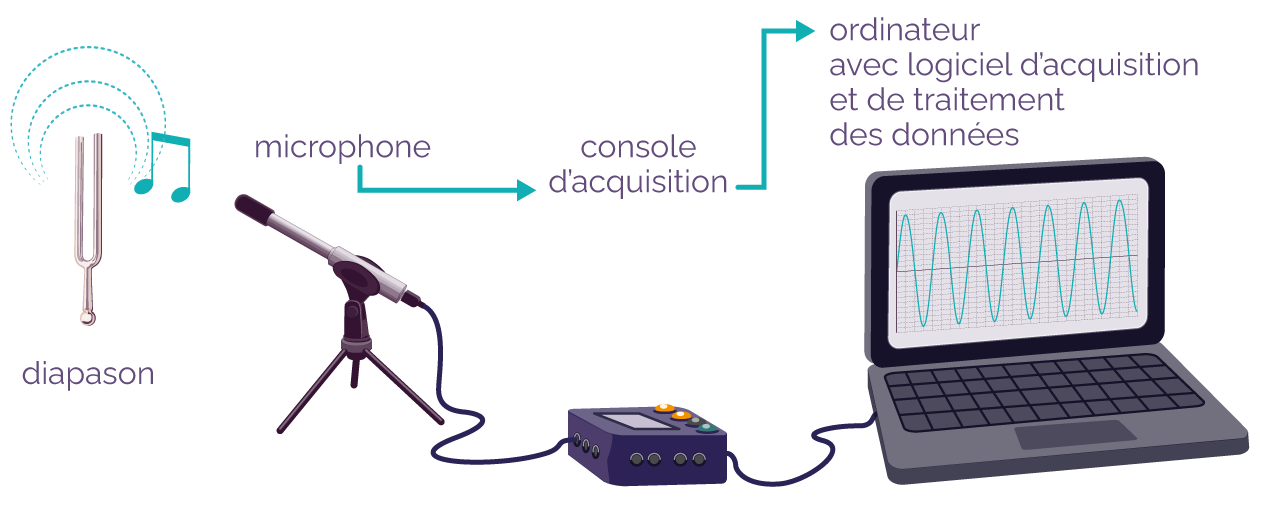Dispositif expérimental permettant de visualiser l’amplitude d’un son

On réalise l’enregistrement de l’amplitude du son en fixant la durée d’enregistrement ainsi que le nombre de points d’acquisition sur cette durée. Le nombre de points d’acquisition correspond au nombre de mesures effectuées pendant la durée d’acquisition.

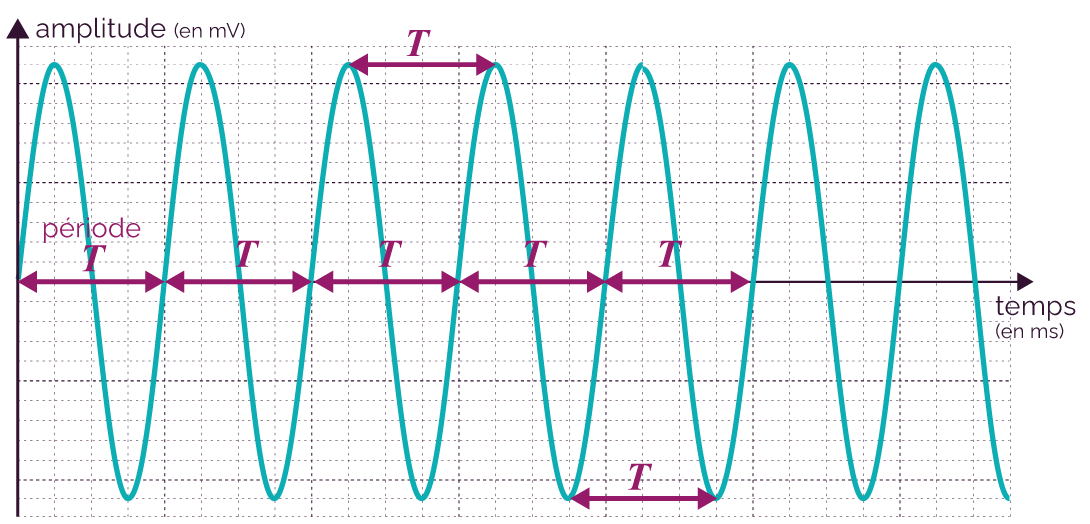Enregistrement de l’évolution de l’amplitude sonore en fonction du temps

La courbe obtenue est une sinusoïde, caractéristique des sons purs. Un son est pur si son évolution temporelle est une sinusoïde.

Le son émis par le diapason est donc un son pur.

Détermination de la période du son produit par un diapason

La sinusoïde est une courbe qui se répète identique à elle-même à des intervalles de temps égaux. Chaque intervalle est appelé période temporelle T.

Le son émis par le diapason est donc périodique.

Méthodes

Pour déterminer graphiquement la période T, il y a deux méthodes. On peut :

soit mesurer directement celle-ci sur la courbe enregistrée ;
soit mesurer un intervalle de temps correspondant à N périodes puis diviser cette durée par N pour trouver la période T. Cette seconde méthode permet d’obtenir une mesure plus précise.

Exemple
Sur l’enregistrement précédent, on mesure la durée

correspondant à cinq périodes. On obtient :

= 11,36 ms.
On calcule alors la période T : T =

= 2,272 ms.

Détermination de la fréquence du son produit par un diapason

Par définition, la fréquence f est égale au nombre de périodes temporelles T contenues dans une seconde. Son unité est le hertz (Hz). Sa formule est la suivante :

f est en hertz (Hz) et T est en seconde (s).

Remarque
On utilise parfois les multiples du hertz ou les sous-multiples de la seconde.

kilohertz : 1 kHz = 10³ Hz ;
mégahertz : 1 MHz = 10⁶ Hz ;
gigahertz : 1 GHz = 10⁹ Hz ;
milliseconde : 1 ms = 10^-3 s ;
microseconde : 1 s = 10^-6 s ;
nanoseconde : 1 ns = 10^-9 s.

Exemple
Pour l’enregistrement précédent, on convertit la période T en seconde puis on calcule la fréquence f.
On obtient : T = 2,272 ms = 2,272

10^-3 s.
On calcule alors la fréquence f :

Le la 440 fait référence en fait à la valeur en hertz de la fréquence du son émis par le diapason.

b. Les sons composés, l'exemple de la flute à bec

Une flute est un instrument de musique à vent très répandu et que l’on peut trouver sous différentes forme : flute à bec, flute traversière, flute de Pan...

Visualisation du son produit par une flute à bec

On visualise le son émis par une flute à bec avec le même dispositif expérimental que celui utilisé pour le diapason.

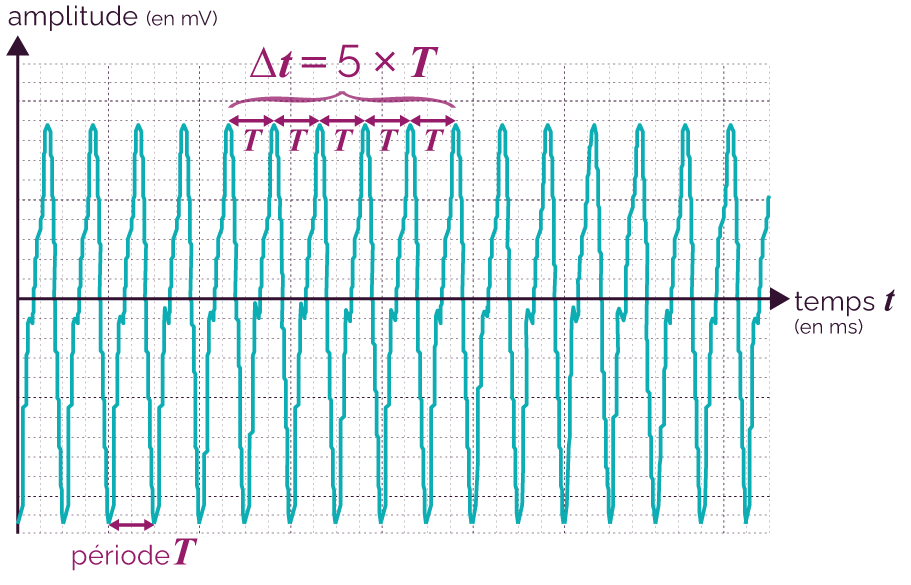Enregistrement de l’évolution de l’amplitude sonore en fonction du temps

On constate que ce son est périodique car la courbe se reproduit identique à elle-même à des intervalles de temps réguliers.

Détermination de la période et de la fréquence du son produit par une flute à bec

On mesure la durée correspondant à cinq périodes. On obtient : = 15,0 ms. On calcule alors la période T : T = = 3,00 ms.

On convertit la période T en seconde puis on calcule la fréquence f.

On obtient : T = 3,00 ms = 3,00 10^-3 s. On calcule alors la fréquence f :

Analyse du son produit par une flute à bec

On constate que la courbe n’est pas une sinusoïde, ce son n’est donc pas un son pur.

On montre que ce son résulte de la superposition de plusieurs sinusoïdes en réalisant le spectre en fréquence de celui-ci. Le spectre en fréquence correspond à un diagramme où sont indiquées en abscisse les fréquences des sons sinusoïdaux qui composent le son et en ordonnée les amplitudes associées à chaque son sinusoïdal.

On obtient ce spectre par une analyse mathématique de la courbe de l’amplitude sonore en fonction du temps, fournie par le logiciel de traitement des données.

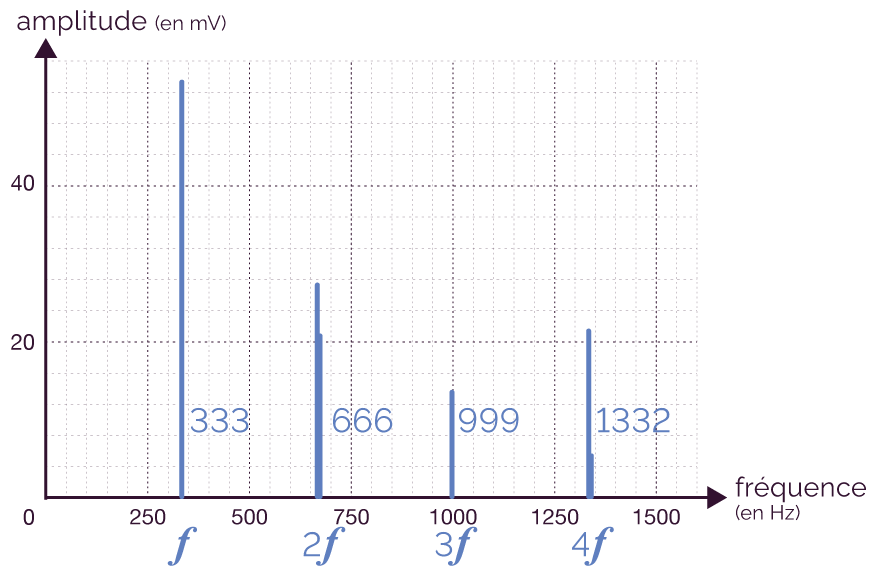Spectre en fréquence du son émis par une flute à bec

Sur le diagramme ci-dessus, chaque barre du spectre correspond à la fréquence d'une des sinusoïdes composant le son.

On constate que le son est composé de quatre sinusoïdes dont les fréquences sont toutes multiples de la première sinusoïde en partant de la gauche. La première des fréquences est égale à la fréquence f calculée du son :
666 Hz = 2 × 333 Hz ; 999 Hz = 3 × 333 Hz ; 1332 Hz = 4 × 333 Hz ;

Sur un spectre en fréquence, la première des fréquences en partant de la gauche est appelée fréquence fondamentale. Les autres sont les harmoniques.
Les harmoniques sont proportionnelles à la fréquence fondamentale.
Un son composé de fréquence f est la somme de plusieurs sons sinusoïdaux dont les fréquences sont des multiples de f.

Le son émis par la flute est donc un son composé.

c. La fabrication d'un son composé

Des logiciels permettent de fabriquer un son composé. Un son composé de fréquence f est synthétisé en superposant (c’est à dire en additionnant) des sons purs de fréquences f, 2f, 3f… Les fréquences des sons purs additionnés sont proportionnelles à la fréquence f.

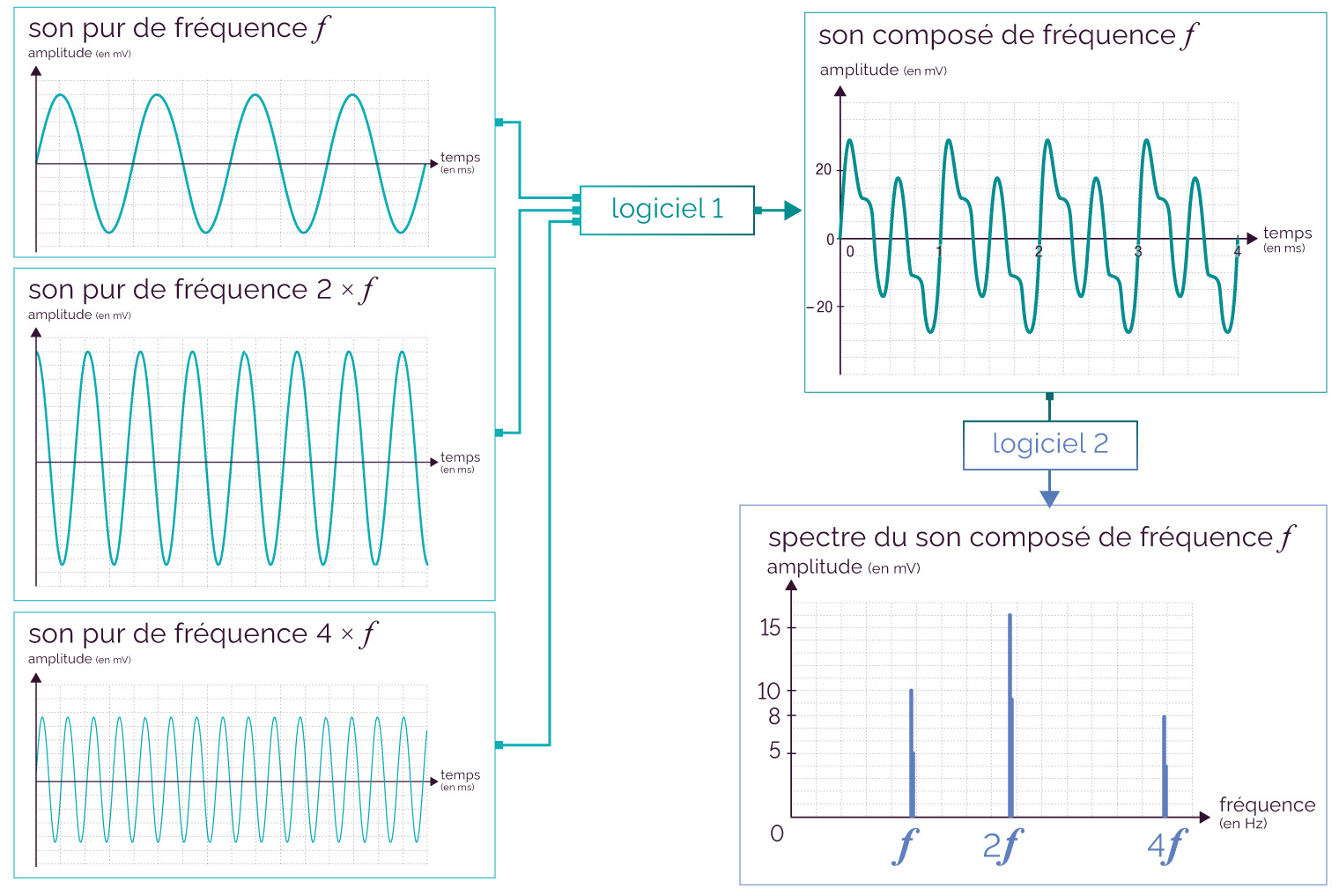Illustration de la synthèse d’un son composé de fréquence f

2. L'intensité sonore et le niveau sonore

Un son transporte de l’énergie. Pour caractériser cette énergie déposée par unité de temps et de surface sur un récepteur, on définit l’intensité sonore. La sensation auditive d’un son est caractérisée par le niveau d’intensité sonore.

a. L'intensité sonore

La puissance sonore P associée à un son est égale à l’énergie sonore déposée chaque seconde sur une surface S. Cette surface peut-être celle d’un microphone ou d’un tympan par exemple. Cette puissance a pour unité le watt (W).

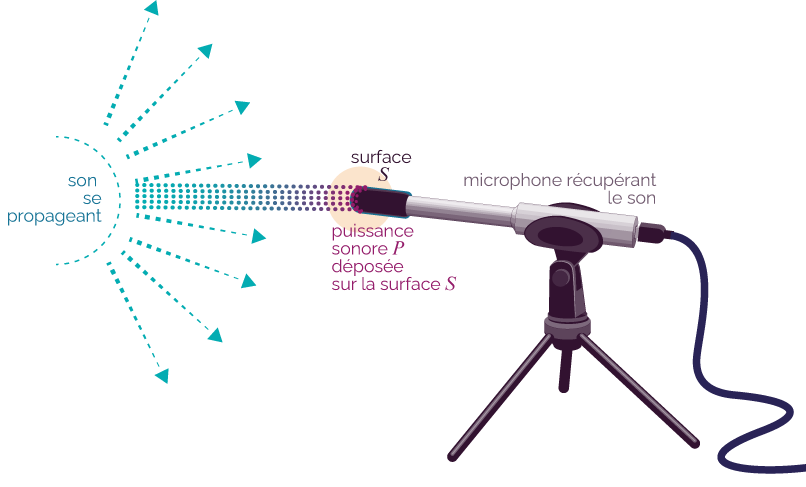Illustration de la puissance sonore déposée sur la surface d’un récepteur sonore

L’intensité sonore I est égale au rapport de la puissance sonore P (en watt) sur la surface S (en mètre carré) : il s’agit donc de la puissance sonore par unité de surface en watt par mètre carré (W.m⁻²).

Cette grandeur permet de comparer des sons différents. Plus un son est perçu comme fort, plus son intensité sonore est forte.
On définit I₀ comme la valeur de l’intensité sonore associée au seuil d’audibilité, qui est la valeur de l’intensité sonore en dessous de laquelle un son n’est plus audible par l’oreille :
I₀ = 1,0 × 10⁻¹² W.m⁻²
On considère un même son enregistré par trois microphones différents placés à la même distance de la source sonore. On donne pour chacun, la puissance sonore déposée et la surface sensible du microphone.

	Micro 1	Micro 2	Micro 3
P (W)	8,0 × 10⁻⁶	4,0 × 10⁻⁶	1,6 × 10⁻⁵
S (m²)	4,0 × 10⁻⁴	2,0 × 10⁻⁴	8,0 × 10⁻⁴

On calcule l’intensité sonore associée :

	Micro 1	Micro 2	Micro 3
I (W.m⁻²)	2,0 × 10⁻²	2,0 × 10⁻²	2,0 × 10⁻²

L’intensité sonore est la même pour chacun des microphones.

On considère un même son enregistré par un même microphone placé à des distances différentes de la source sonore. On donne pour chaque cas, la puissance sonore déposée et la distance du micro. La surface sensible du microphone est égale à 4,0 × 10⁻⁴ mètre carré.

	Micro à d₁	Micro à d₂	Micro à d₃
P (W)	8,0 × 10⁻⁶	2,0 × 10⁻⁶	8,0 × 10⁻⁸
d (m)	1,0	2,0	10,0

On calcule l’intensité sonore associée :

	Micro à d₁	Micro à d₂	Micro à d₃
I (W.m⁻²)	8,0 × 10⁻⁶	1,0 × 10⁻⁶	8,0 × 10⁻⁹

L’intensité sonore est une fonction décroissante de la distance à la source sonore.

Un microphone enregistre le son d’un instrument puis celui d’un second et enfin, enregistre le son produit par les deux instruments en même temps. La surface sensible du microphone est égale à 3,0 × 10⁻⁴ mètre carré. On donne la puissance sonore déposée.

	Instrument 1	Instrument 2	Instruments 1 et 2
P (W)	9,0 × 10⁻⁶	3,0 × 10⁻⁶	1,2 × 10⁻⁵

On calcule l’intensité sonore associée :

	Instrument 1	Instrument 2	Instruments 1 et 2
I (W.m^-2)	3,0 × 10⁻²	1,0 × 10⁻²	4,0 × 10⁻²

L’intensité sonore des deux instruments ensemble est égale à la somme des intensités sonores des deux instruments pris séparément.

b. Le niveau d'intensité sonore

L’intensité sonore peut varier sur une très grande amplitude, de 1,0 × 10^-12 W.m^-2 qui correspond à la valeur limite du seuil d’audibilité d’un son, jusqu’à 10 W.m^-2 qui correspond à la valeur du seuil de la douleur auditive d’un son.
On définit alors une grandeur plus facile à manipuler, le niveau d’intensité sonore qui est défini par la relation suivante :

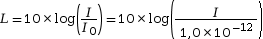
où I est l’intensité sonore et I₀ le seuil d’audibilité.

Le niveau d’intensité sonore a pour unité le décibel (dB). La fonction « log », appelée logarithme, est accessible sur toutes les calculatrices. I₀ est la valeur de l’intensité sonore associée au seuil d’audibilité.

L’intensité sonore variant sur une très grande plage de valeurs (de 10^-12 à 10⁴ W.m^-2 environ), l’intérêt du niveau d’intensité sonore est de pouvoir ramener les valeurs sur un intervalle plus petit et donc plus facile à manipuler.

I (W.m^-2)	10^-12 W.m^-2	10^-5 W.m^-2	10 W.m^-2	10⁴ W.m^-2
L (dB)	0	70	130	160

L’échelle du bruit relie l’intensité sonore et le niveau d’intensité sonore.

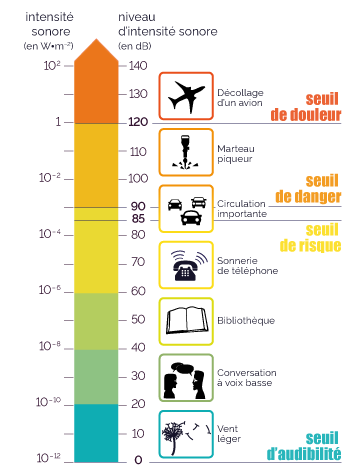Échelle du bruit

On peut calculer l’intensité sonore I associée à un niveau d’intensité sonore L en appliquant la formule suivante :

3. L'étude des instruments à cordes et à vent

Le son d’un instrument de musique peut être produit par la vibration d’une corde (instruments à cordes) ou d’une colonne d’air (instruments à vent).

a. La guitare

Un guitariste doit placer ses doigts sur ou entre les frettes disposées le long du manche de la guitare afin de jouer différentes notes. Faire glisser son doigt le long du manche permet de faire varier la longueur de la corde.

On détermine pour une corde donnée, la fréquence fondamentale du son produit en fonction de la longueur de la corde.

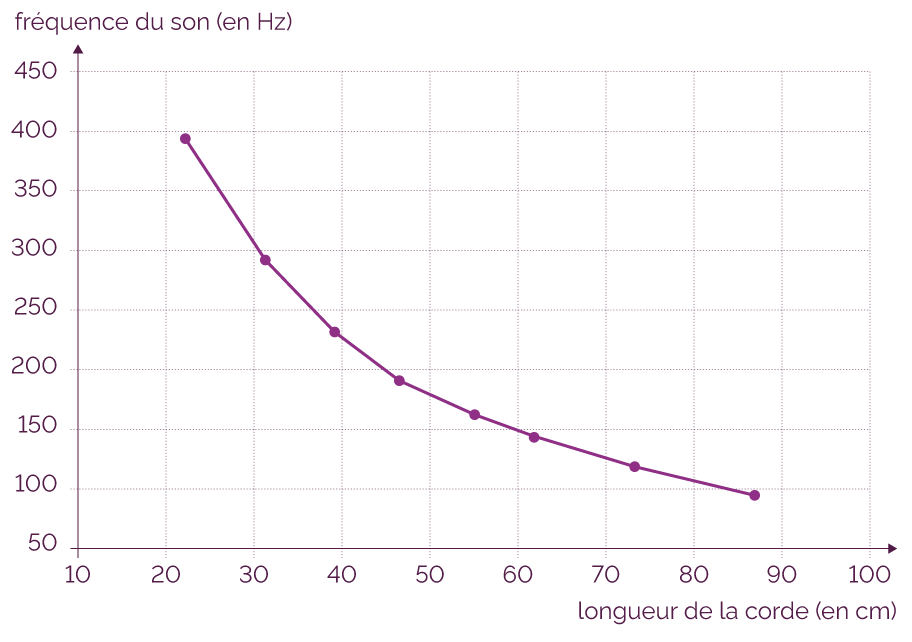Variation de la fréquence de la note jouée en fonction de la longueur de la corde

On constate que la fréquence est une fonction décroissante de la longueur de la corde : plus la corde est longue, et plus la fréquence de la note est basse.

Remarque
Plus la fréquence de la note est basse et plus la note jouée est grave.

La tension de la corde joue un rôle.

Plus la tension de la corde est grande, pour une longueur de corde fixée, et plus la fréquence de la note jouée est élevée.

La masse linéique de la corde joue un rôle.

La masse linéique de la corde est égale à la masse de celle-ci par unité de longueur. Elle a pour unité le gramme par centimètre (g.cm^-1).
Plus la masse linéique de la corde est grande, pour une longueur de corde fixée, et plus la fréquence de la note jouée est basse.

b. La flute

Un flutiste doit placer ses doigts sur les trous disposés le long du corps de la flute afin de jouer différentes notes. On peut faire varier la longueur de la colonne d’air à l’intérieur de l’instrument.

La longueur de la colonne d’air joue un rôle : plus la colonne d’air est longue et plus le son produit possède une fréquence basse (le son est alors plus grave).