Le rayonnement solaire
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Déterminer la masse solaire transformée chaque seconde en énergie à partir de la donnée de la puissance rayonnée par le Soleil.
- Déterminer la longueur d’onde d’émission maximale à partir d’une représentation graphique du spectre d’émission du corps noir à une température donnée.
- Déterminer la température de surface d’une étoile à partir de la longueur d’onde d’émission maximale en appliquant la loi de Wien.
- Identifier sur un schéma les configurations pour lesquelles la puissance reçue par une surface est maximale ou minimale.
- Analyser, interpréter et représenter graphiquement des données de températures.
- L’énergie dégagée par les réactions de fusion de l’hydrogène, qui se produisent dans les étoiles, les maintient à une température très élevée. Du fait de l’équivalence masse-énergie (relation d’Einstein), ces réactions s’accompagnent d’une diminution de la masse solaire au cours du temps.
- Comme tous les corps matériels, les étoiles et le Soleil émettent des ondes électromagnétiques et donc perdent de l’énergie par rayonnement.
- Le spectre du rayonnement émis par la surface (modélisé par un spectre de corps noir) dépend seulement de la température de surface de l’étoile.
- La longueur d’onde d’émission maximale est inversement proportionnelle à la température absolue de la surface de l’étoile (loi de Wien).
- La puissance radiative reçue du Soleil
par une surface plane est proportionnelle à
l’aire de la surface et dépend de
l’angle entre la normale à la surface et la
direction du Soleil. Ainsi, la puissance solaire
reçue par unité de surface terrestre
dépend :
- de l’heure (variation diurne) ;
- du moment de l’année (variation saisonnière) ;
- de la latitude (zonation climatique).
- Énergie.
- Puissance.
Le Soleil est une étoile, assimilable à une
sphère, dont le diamètre est égal
à environ 1,4 millions de kilomètres
(1,4×106 km).
Il est principalement composé
d’hydrogène (75 % de sa masse) et
d’hélium (25 % de sa masse). C’est la
source d’énergie rayonnante du
système solaire.
Photographie du Soleil
Dans le cœur du Soleil ont lieu des réactions nucléaires de fusion. La fusion est un processus pendant lequel deux noyaux atomiques légers entrent en collision et forment un noyau atomique plus lourd.
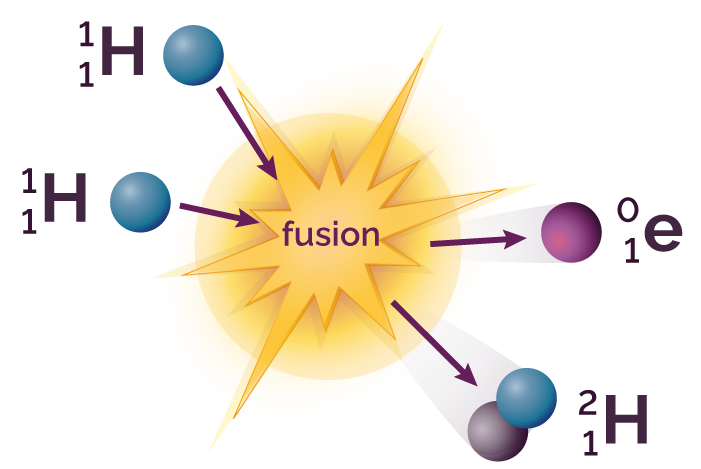
Réaction de fusion entre deux noyaux d'hydrogène 1
Ici, le noyau d’hydrogène 2 formé est plus lourd que les deux noyaux d’hydrogène 1 qui ont fusionné. Pour le vérifier, il suffit de comparer leurs nombres de masse respectifs : 2 est supérieur à 1.
Les réactions de fusion ne sont possibles que sous certaines conditions de température et de pression. La température doit être supérieure ou égale à environ 10 millions de degrés celsius (1,0×107 °C), ce qui est le cas dans les couches centrales du Soleil.
En astrophysique (science qui étudie notamment le fonctionnement des étoiles), les scientifiques utilisent comme unité de température le kelvin (K).
La relation entre la température T en kelvin (K) et la température t en degrés celsius (°C) est la suivante :
Le Soleil produit de l’énergie grâce à une série de réactions de fusion dont le bilan s’écrit :
Quatre noyaux d’hydrogène 1
( 
) se transforment en un
noyau d’hélium 4 ( 
) plus lourd. Il se
forme également deux photons ( γ ), deux positons
( 
) et deux neutrinos
( ν ).
- Le photon est la particule élémentaire du rayonnement électromagnétique. Il porte la plus grande partie de l’énergie produite lors de la réaction de fusion.
- Le positon est l’antiparticule de l’électron. Il possède les mêmes caractéristiques que l’électron, hormis sa charge électrique : le position a une charge positive tandis que l’électron a une charge négative.
- Le neutrino est une particule élémentaire qui possède une charge nulle et une masse extrêmement petite.
On constate que la somme des masses des noyaux réactifs est supérieure à la somme des masses du noyau et des particules produits.
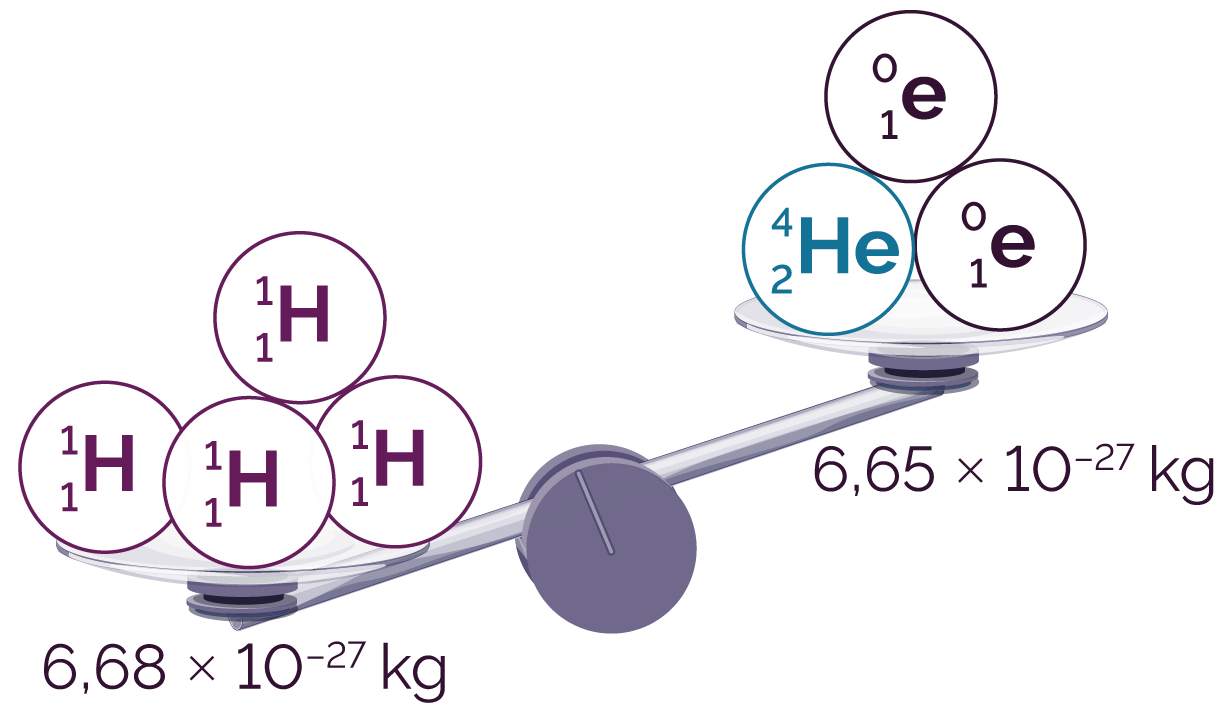
Comparaison des masses des réactifs et des produits
La masse du photon est nulle et celle du neutrino est négligeable.
La perte de masse pendant la réaction de fusion est à l’origine d’une libération d’énergie. Pour calculer la quantité d’énergie libérée, on utilise la relation d’Einstein.
La relation s’écrit de la façon suivante :
|
E = m × c2 |
avec :
|
Le coefficient de proportionnalité est donc égal au carré de la vitesse de la lumière dans le vide.
La variation de masse Δm au cours de la réaction de fusion permet de calculer la variation d’énergie ΔE du système nucléaire.
|
ΔE = Δm × c2 |
avec :
|
La variation de masse Δm a pour expression :
Δm = mproduits – mréactifs
Comme mproduits< mréactifs, Δm est négative donc ΔE est, elle aussi, négative. Cela signifie que le système nucléaire perd (et donc libère) de l’énergie.
L’énergie libérée au cours de la réaction de fusion, comptée positivement, se calcule en utilisant la valeur absolue avec la relation suivante :
ǀΔEǀ = ǀΔmǀ × c2
La valeur absolue d’un nombre x est égale à sa valeur positive :
ǀxǀ = x si x est positif et ǀxǀ = –x si x est négatif
Application
On cherche à calculer l'énergie
libérée ǀΔEǀ pour la
série de réactions de fusion dont le
bilan est le suivant :
Les masses des réactifs et des produits sont
données :
mréactifs=
6,68×10–27
kg et mproduits=
6,65×10–27
kg.
On calcule d’abord la perte de masse Δm :
Δm =
mproduits–
mréactifs=
6,65×10–27–
6,68×10–27=
–3×10–29
kg
On calcule ensuite l’énergie
libérée ǀΔEǀ:
ǀΔEǀ = ǀΔmǀ×c2= ǀ–3×10–29ǀ×(3,00×108)2=
3×10–12 J
On a vu précédemment que le Soleil libérait (et donc perdait) de l’énergie sous la forme d’un rayonnement électromagnétique.
La puissance rayonnée par le Soleil, notée PS, correspond à l’énergie libérée par les réactions de fusion par unité de temps. On a la relation suivante :
|
|
avec :
|
La relation d’Einstein permet de relier la puissance rayonnée par le Soleil PS à la masse solaire mS transformée chaque seconde en énergie :
On peut ainsi calculer la masse solaire mS transformée chaque seconde à partir de la donnée de la puissance rayonnée par le Soleil PS.
|
|
avec :
|
Application
La puissance rayonnée par le Soleil est
donnée : PS= 4×1026 W. La
masse solaire transformée chaque seconde est
égale à :
Chaque seconde, le Soleil perd donc une masse de 4 milliards de kilogrammes.
- Un rayonnement
électromagnétique est
caractérisé par sa longueur
d’onde λ,
exprimée en nanomètre (nm). Chaque
rayonnement électromagnétique
appartient à un domaine de longueur
d’onde.
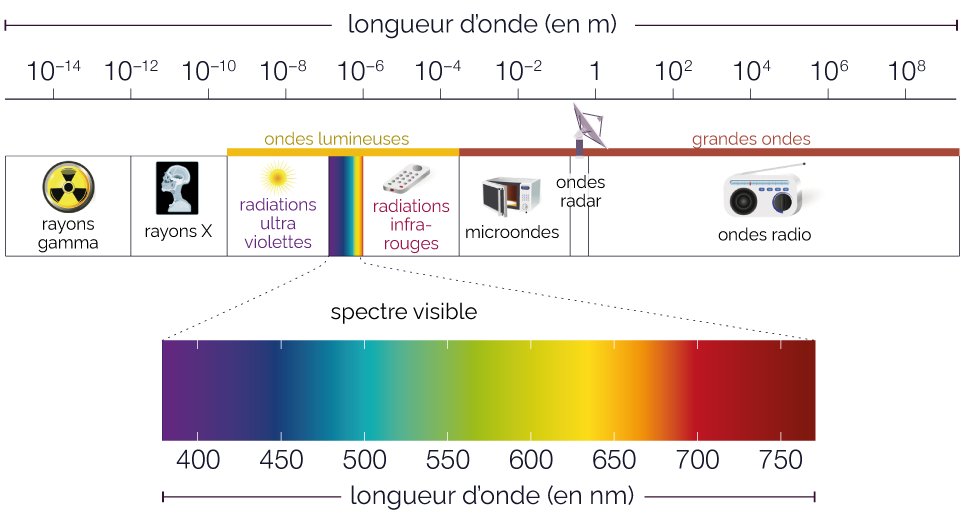
Spectre des ondes électromagnétiques - Le spectre d’émission d’un corps correspond à la courbe de l’intensité du rayonnement émis par ce corps en fonction de la longueur d’onde du rayonnement émis.
Pour simplifier l’interprétation des phénomènes d’absorption et d’émission de lumière dans l’espace, on définit un objet idéal appelé corps noir. Il est capable d’absorber tous les rayonnements, quelles que soient leurs longueurs d’onde.
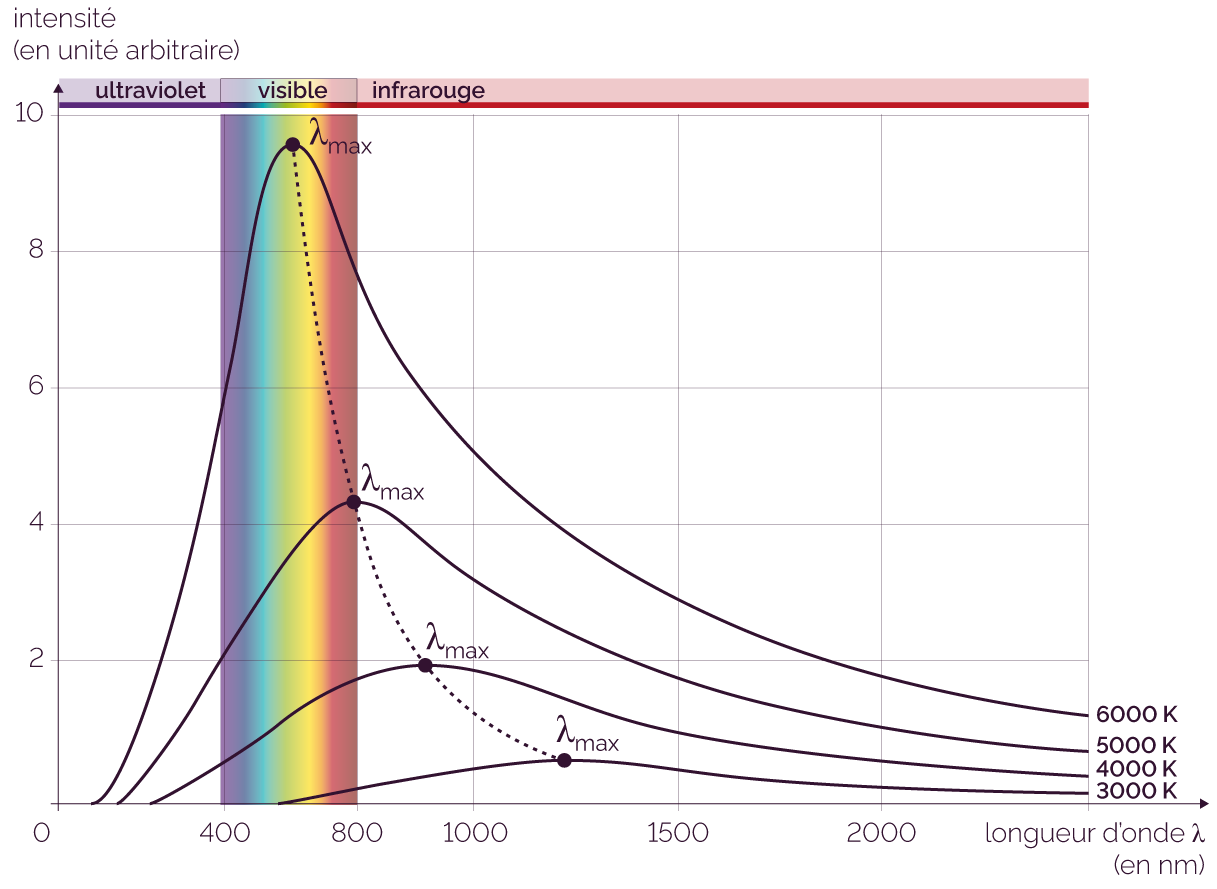
Spectre d'émission du corps noir pour différentes températures
Sur le graphique, pour une température de surface de 6000 K, l’absorption maximale est située dans le vert ; alors que pour une température de surface de 5000 K, elle est située dans le rouge.
On remarque donc que pour un corps noir donné, la longueur d’onde correspondant au maximum d’absorption (λmax) est une fonction décroissante de la température.
Par ailleurs, la loi de Wien donne la relation suivante :
|
|
avec :
|
Application
Le spectre d’émission du Soleil est le
suivant :
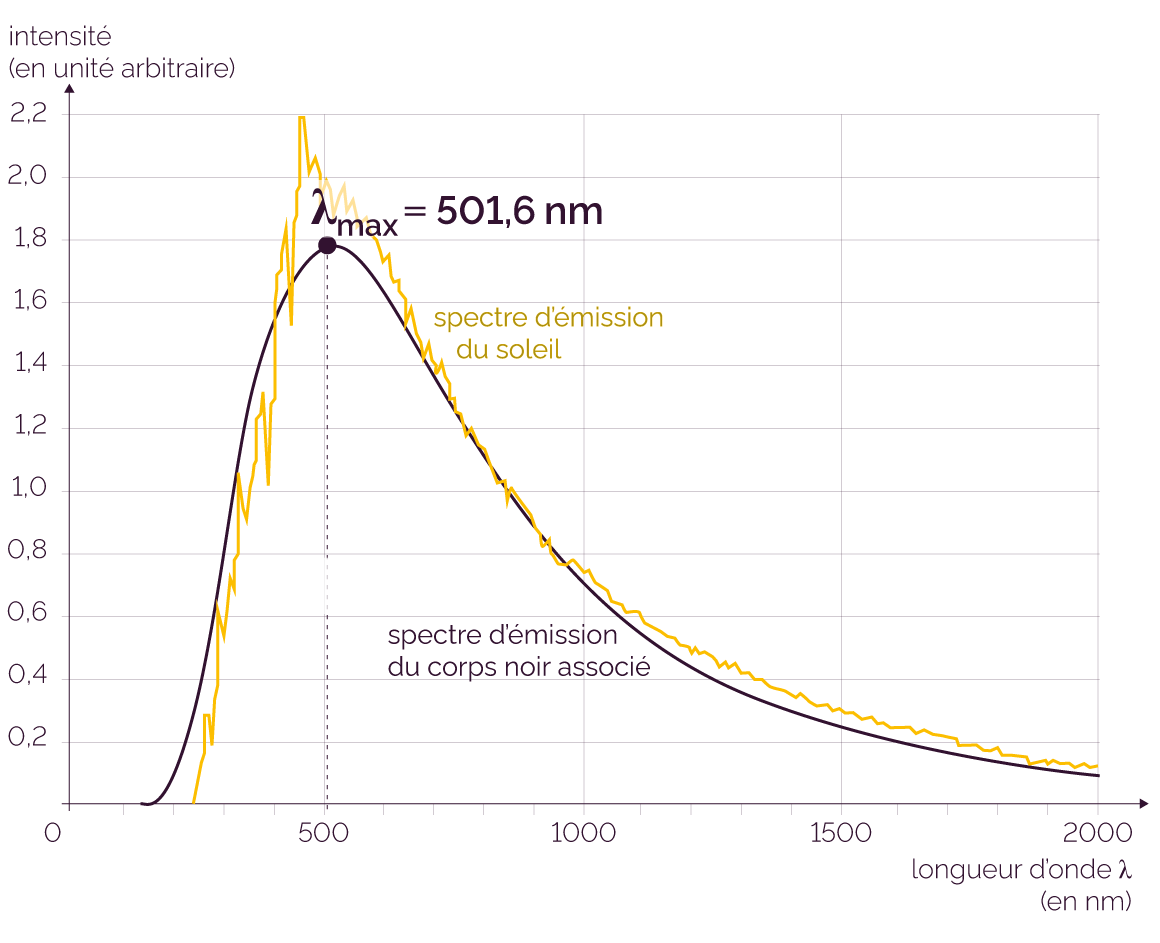
Spectre d'émission du Soleil
On lit la longueur d’onde d’émission
maximale sur le graphique : λmax = 501,6
nm.
On applique la loi de Wien pour trouver la
température de surface T du Soleil :
La température de surface du Soleil est donc de 5778 kelvins.
N’importe quelle surface sur Terre reçoit une certaine puissance radiative en provenance du Soleil.
Elle a comme unité le watt (W).
La valeur de cette puissance dépend de certains paramètres.
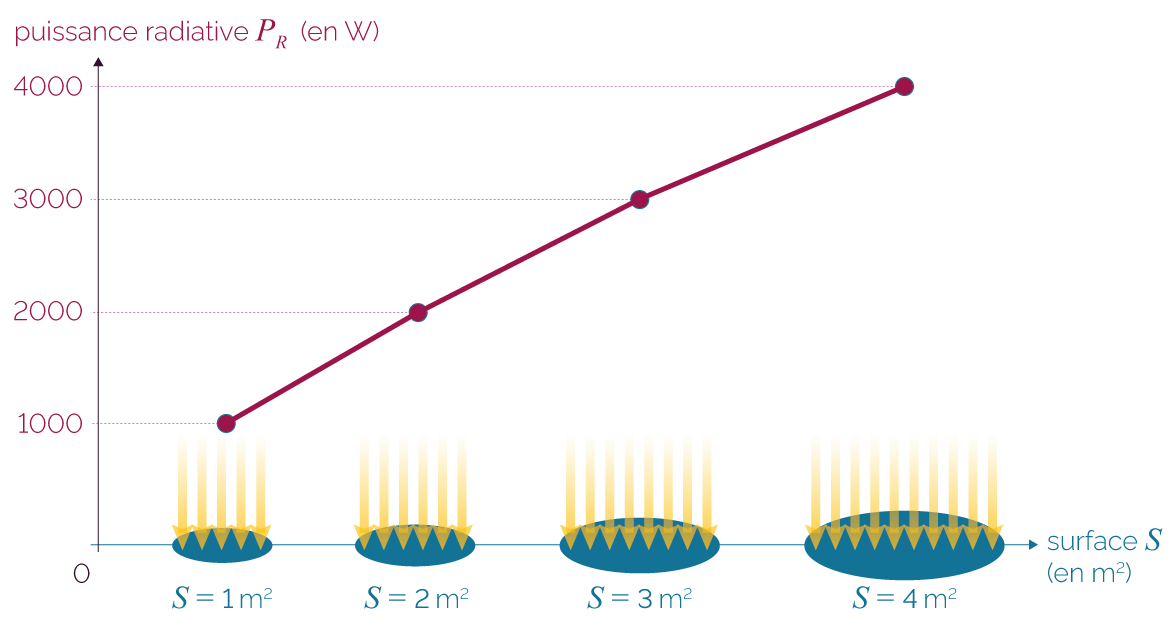
Puissance radiative PR reçue pour différentes aires de surface
Le soleil étant très éloigné de la Terre, tous les rayons solaires sont parallèles entre eux.
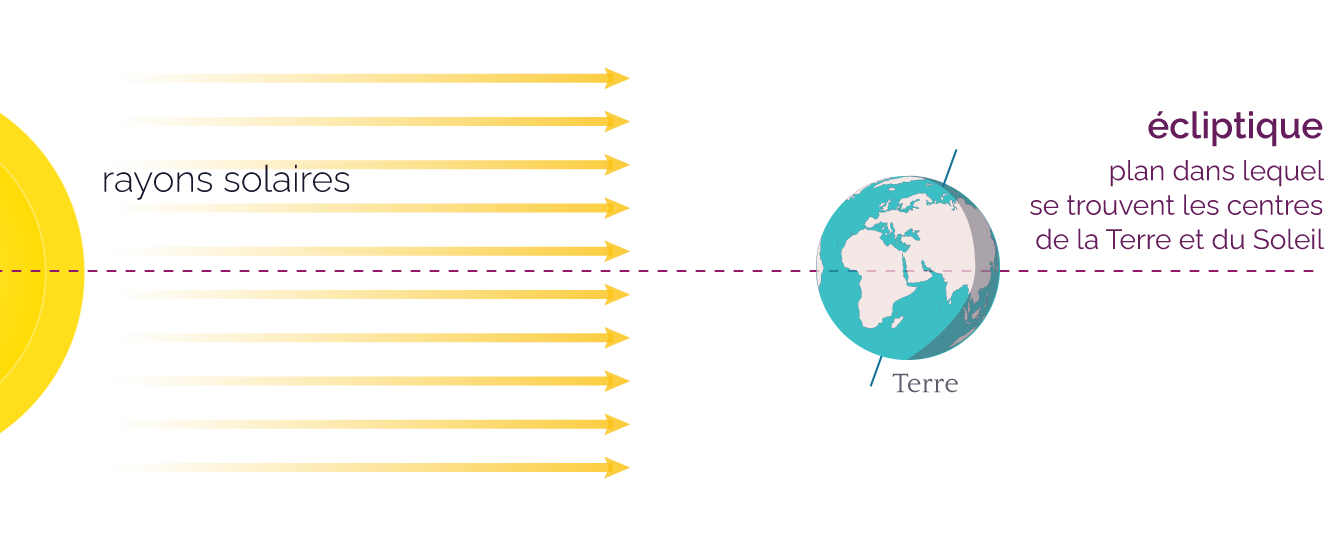
On appelle normale à la surface la droite perpendiculaire à la surface. Elle forme donc un angle de 90° avec cette surface.
On définit l’angle d’inclinaison α comme celui formé par la normale à la surface S et la direction des rayons solaires
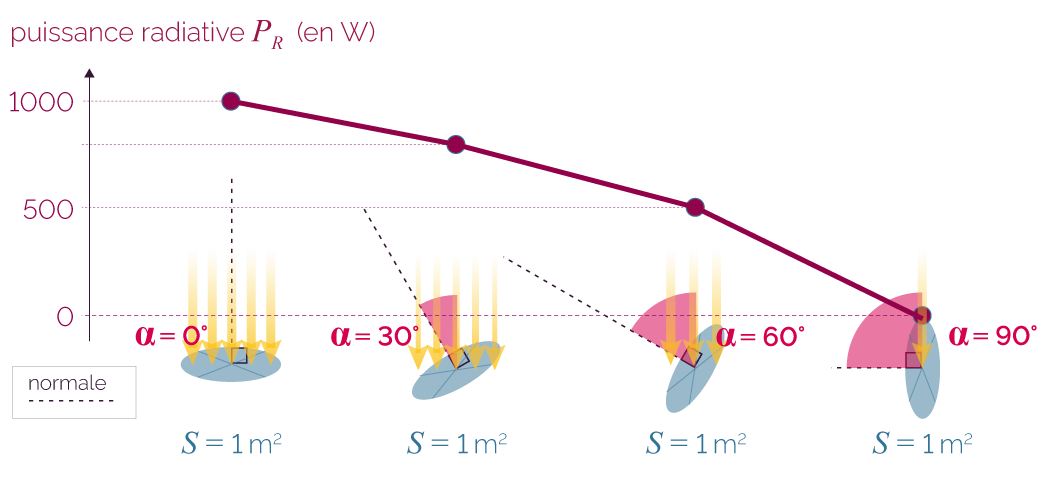
Puissance radiative PR reçue selon l'angle d'inclinaison α
La puissance radiative diminue lorsque l’angle d’inclinaison α augmente. Elle est maximale pour α = 0°, ce qui correspond à des rayons arrivant perpendiculairement à la surface, et minimale pour α = 90°, ce qui correspond à des rayons arrivant parallèlement à la surface.
On définit la puissance solaire reçue du Soleil par unité de surface PuS avec la relation suivante :
|
|
avec :
|
Cette grandeur varie en fonction d’un certain nombre de paramètres.
Au cours d’une journée, la hauteur du Soleil dans le ciel varie, ce qui induit une variation de l’angle d’inclinaison α des rayons solaires.
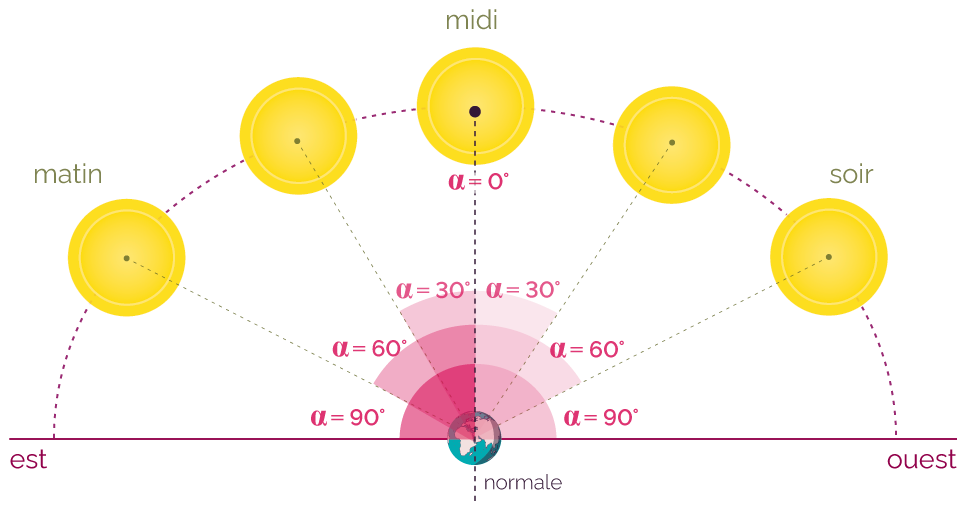
Variation de l'angle d'inclinaison α au cours de la journée
La variation de l’angle d’inclinaison α des rayons solaires au cours de la journée montre que la puissance solaire reçue du Soleil par unité de surface PuS est maximale à midi et s’annule au lever et au coucher du Soleil.
Au cours de l’année, à une même heure de la journée, la hauteur du Soleil est différente selon les mois et l’angle d’inclinaison α des rayons solaires varie donc également.
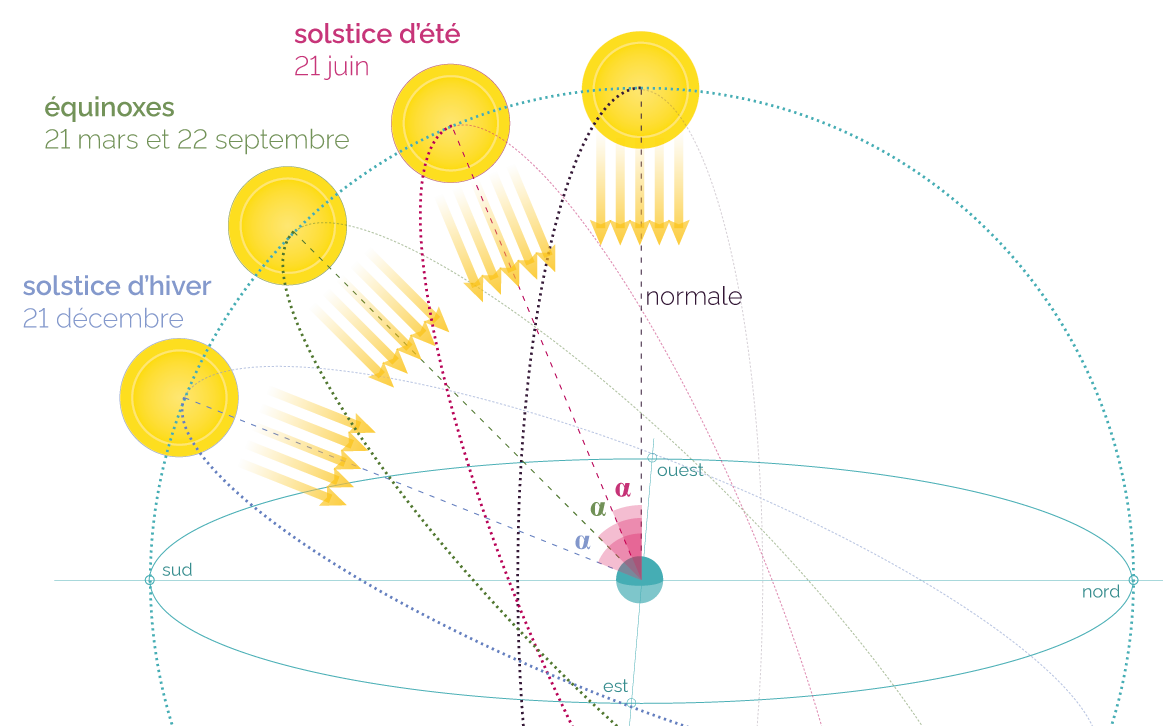
L'angle d'inclinaison α au midi solaire à différentes dates de l'année
dans l'hémisphère Nord
Pour un point de l’hémisphère Nord, on peut établir la relation d’ordre suivante :
α(solstice d’été) < α(équinoxes) < α(solstice d’hiver)
La variation de l’angle d’inclinaison α au cours de l’année, pour une même heure de la journée, montre que la puissance solaire reçue du Soleil par unité de surface PuS est maximale au solstice d’été et minimale au solstice d’hiver, pour un point du globe situé dans l’hémisphère Nord.
Pour un point de l’hémisphère Sud, on observerait le contraire. Ceci s’explique par l’inclinaison de l’axe de rotation de la Terre sur elle-même par rapport au plan de l’écliptique (voir la partie III).
La latitude λ est une coordonnée géographique associée à la valeur d’un angle. Elle représente la position d’un point du globe par rapport au plan équatorial, qui est le plan de référence (λ = 0°).
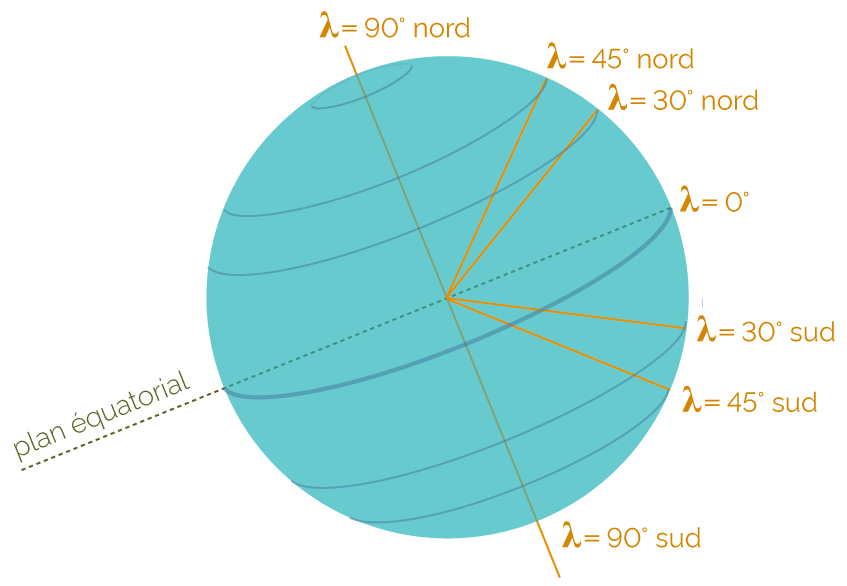
Latitude de quelques points du globe
Aux équinoxes de printemps et d’automne, les rayons solaires arrivent perpendiculairement à la surface de la Terre au niveau de l’équateur.
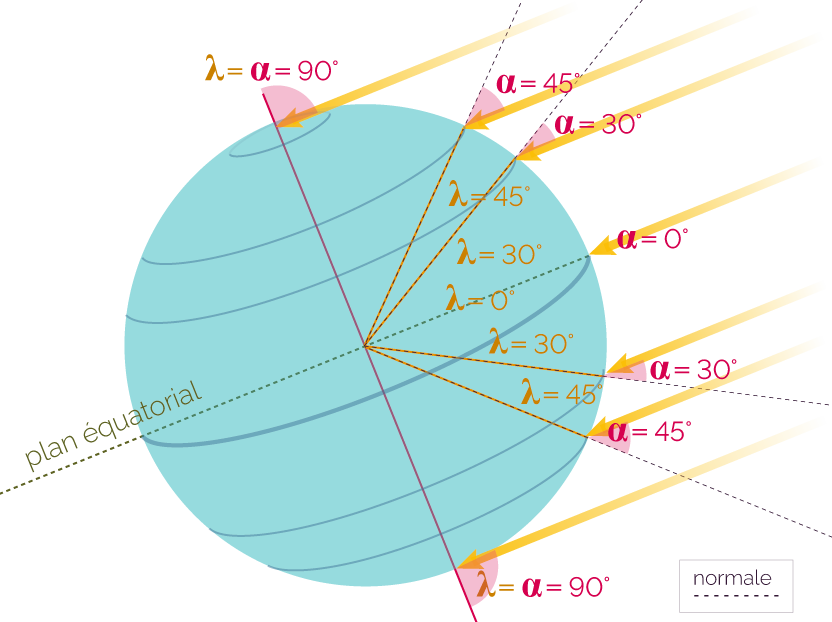
Arrivée des rayons solaires à la surface de la Terre
aux équinoxes de printemps et d’automne
Dans cette configuration, l’angle
d’inclinaison α est égal
à la latitude λ du point du
globe.
On en déduit que la puissance solaire
reçue du Soleil par unité de surface
PuS est :
- maximale à l’équateur car l’angle d’inclinaison α (et donc la latitude λ) est minimale (λ = α = 0°) ;
- minimale aux pôles Nord et Sud car l’angle d’inclinaison α (et donc la latitude λ) est maximale (λ = α = 90°).
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Sciences
Une conversion naturelle de l'énergie solaire : la photosynthèse
Sciences
Le bilan thermique du corps humain
Sciences
Entendre la musique
Sciences
Le bilan radiatif terrestre
Sciences
La forme de la Terre
Sciences
Formation des images sur la rétine - Nécessité de l'accommodation
Sciences
Biologie des microorganismes et conservation des aliments
Sciences
Qualité des sols et de l'eau
Sciences
Pratiques alimentaires, collectives et perspectives globales
Sciences
Se nourrir au quotidien : exemple des émulsions
Sciences
Conditions de visibilité d'un objet
Sciences
Lentilles minces convergentes et divergentes
Sciences
Couleur et Art
Sciences
Les perturbations chimiques de la perception visuelle
Sciences
Comportements sexuels
Fermer
Accédez gratuitement à
