Equations de droites
- Fiche de cours
-
Quiz et exercices
1
- Vidéos et podcasts
Comment définit-on une droite par son équation ? Comment tracer une droite à partir de son équation ? Comment déterminer l'équation d'une droite à partir d'une représentation graphique ? Comment déterminer l'équation d'une droite à partir des coordonnées de 2 points distincts ?
1) x = c où c est un nombre réel, si elle est parallèle à l'axe de ordonnées
2) y = px + d où p et d sont des nombres réels, si elle n'est pas parallèle à l'axe des ordonnées
Remarque : On rencontrera parfois des équations du type ay + bx + c = 0 avec a ≠ 0. On pourra alors les transformer en une équation du type y = px + d que l’on appelle équation réduite de la droite.
Exemples :
a) y = 3x + 2 est l’équation d’une droite non parallèle à l’axe des ordonnées
b) x = 3 est l’équation d’une droite parallèle à l’axe des ordonnées
c) 2y - 2x + 4 = 0 est aussi une équation de droite, en effet
p est le coefficient directeur de la droite ;
d est l’ordonnée à l’origine de la droite.
Exemples :
a) y= 3x + 2 est la droite de coefficient directeur 3 et d’ordonnée à l’origine 2 ;
b) y = x - 2 est la droite de coefficient directeur 1 et d’ordonnée à l’origine -2.
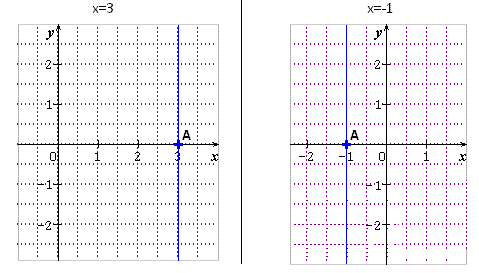
* Cas où x = c
Il s’agit de la droite parallèle à l’axe des ordonnées passant par le point A(c ;0).
Exemples :
* Cas y = px + d à partir des coefficients
D’après ce qui précède :
* d est l’ordonnée à l’origine de la droite, c’est donc l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées. Le point de coordonées (0 ;d) appartient à cette droite.
* p est le coefficient directeur de la droite, c'est-à-dire qu’il donne l’accroissement de y pour un accroissement de x valant 1.
Remarque : si p > 0, la droite « monte » et si p < 0, la droite « descend ».
Exemples : Tracer les droites suivantes à partir de leurs équations :
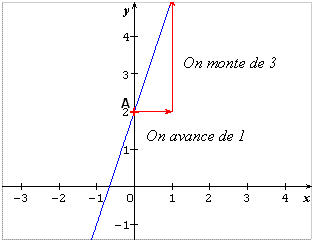
1) y = 3x + 2. L’ordonnée à l’origine est 2. Le point A(0 ;2) appartient à la droite.
Le coefficient directeur est 3. Donc « si on avance de 1 en abscisse, on monte de 3 en ordonnée ».
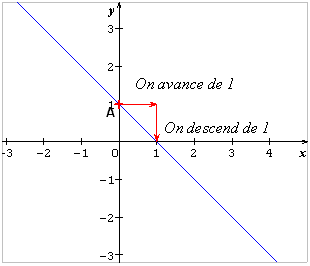
2) y= -x + 1. L’ordonnée à l’origine est 1. Le point (0 ;1) appartient à la droite.
Le coefficient directeur est -1. Donc si on « avance de 1 en abscisse », on « descend de 1 en ordonnée ».
* Cas y = px + d. A partir de deux valeurs distinctes de x.
On choisit deux valeurs différentes pour x. Pour faciliter les calculs, on prend souvent
x = 0 et x = 1. On obtient donc les coordonnées de 2 points distincts de la droite, il ne reste plus qu’à tracer la droite les reliant.
Exemples :
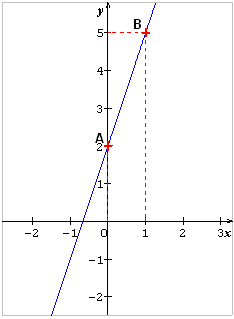
1) y = 3x + 2.
| Valeurs de x | 0 | 1 |
| y = 3x + 2 |
|
|
Les points A(0 ;2) et B(1 ;5) appartiennent à la droite. On trace donc la droite passant par ces 2 points.
2) y = - x + 1
| Valeurs de x | 0 | 1 |
| y = - x + 1 | - 0 + 1 = 1 | - 1 + 1 = 0 |
Les points A(0 ;1) et B(1 ;0) appartiennent à la droite. On trace donc la droite passant par ces 2 points.
et 
appartiennent à
cette droite.
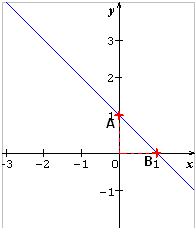
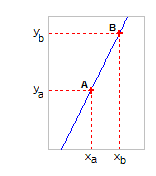
But : trouver les coefficients p et d.
Détermination du coefficient directeur de la droite :
Détermination de l’ordonnée à l’origine : Il suffit de lire l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées.
Exemples : Déterminer les équations des droites suivantes
1)
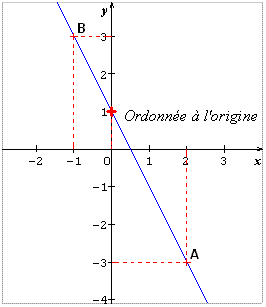
La droite passe par les points A(2 ;-3) et B(-1 ;3)
L’ordonnée à l’origine est 1. Donc d = 1.
L’équation de la droite est : y = -2x + 1.
2)
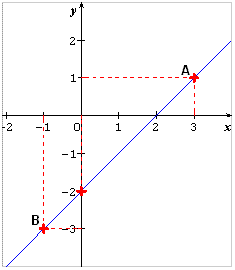
L’ordonnée à l’origine est -2. Donc d=-2.
L’équation de la droite est : y = x - 2.
et appartiennent à
cette droite.
But : trouver les coefficients p et d.
Détermination du coefficient directeur de la droite :
Détermination de l’ordonnée à l’origine : Le point A appartient à la droite, ses coordonnées vérifient l’équation y = px + d. D’où l’obtention de d par la résolution d’une équation.
Exemples : Déterminer les équations suivantes
1) Equation de la droite passant par A(2 ;-3) et B(-1 ;3) :
Elle est de la forme y = px + d
Calcul de
A(2 ;-3) appartient à la droite,
donc
L’équation de la droite est : y = -2x + 1
2) Equation de la droite passant par A(3 ;1) et B(-1 ;-3)
Elle est de la forme y= px + d
Calcul de
A(3 ;1) appartient à la droite,
Donc
.L’équation de la droite est : y = x - 2
Évalue ce cours !
Teste dès maintenant tes nouvelles connaissances dans notre quiz
Vous avez obtenu75%de bonnes réponses !
Reçois l’intégralité des bonnes réponses ainsi que les rappels de cours associés
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Mathématiques
Parallélisme et positions relatives de droites et de plans
Mathématiques
Droite numérique et intervalles
Mathématiques
La valeur absolue
Mathématiques
Les ensembles de nombres
Mathématiques
Nombres pairs et impairs
Mathématiques
Les nombres premiers
Mathématiques
Les calculs avec la racine carrée
Mathématiques
Distance entre deux points et coordonnées du milieu d'un segment
Mathématiques
Les configurations du plan
Mathématiques
Aires et volumes - formulaire
Fermer
Accédez gratuitement à
