Simulation d'une expérience aléatoire et fluctuation de l'échantillonnage
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Simuler une expérience aléatoire à deux issues avec un tableur.
- Connaitre la notion d’échantillon de taille n pour une expérience aléatoire à deux issues.
- Connaitre la notion de fluctuation de l’échantillonnage.
- Connaitre le lien entre la taille des échantillons et l’amplitude des fluctuations.
- Compter le nombre de fréquences de succès situées dans un intervalle.
- Simuler une expérience aléatoire, c’est remplacer cette expérience par une autre plus simple à organiser et qui permet d’obtenir des résultats semblables. L’outil informatique, notamment le tableur, peut être utilisé.
- Des échantillons de la même expérience aléatoire peuvent donner des résultats très différents. C’est ce que l’on appelle la fluctuation de l’échantillonnage.
- Plus la taille des échantillons est grande, plus l’amplitude des fluctuations diminue.
- Pour diviser la dispersion des données par k, il faut multiplier la taille de l’échantillon par k².
- L’écart type de la série des
fréquences est de l’ordre de
.
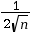- Si on étudie une simulation de N
échantillons de taille
n, que l’on note s l’écart
type de la série des fréquences de
succès et p la probabilité de
succès, on a :
- en moyenne, environ 68 % des fréquences de succès sont dans l’intervalle [p – s ; p + s] ;
- en moyenne, environ 95 % des fréquences de succès sont dans l’intervalle [p – 2s ; p + 2s] ;
- en moyenne, environ 99 % des fréquences de succès sont dans l’intervalle [p – 3s ; p + 3s].
- Lire un graphique
Il n’est pas toujours facile d’organiser une expérience aléatoire. Par exemple, jouer à la roulette nécessite de se déplacer dans un casino ou d’acheter un matériel couteux.
- Avec un tableur, on peut facilement simuler le lancer d’une pièce équilibrée. En effet, la fonction qui donne au hasard un nombre réel compris entre 0 et 1 exclu est : ALEA(). On peut décider arbitrairement qu’à chaque lancer, obtenir 0 équivaut à « pile » et obtenir 1 équivaut à « face ».
- Pour obtenir la partie entière d'un nombre, on utilise la fonction ENT().
- Pour obtenir au hasard un nombre entier compris entre 0 et 1 inclu, on tapera dans le tableur : =ENT(2*ALEA()).
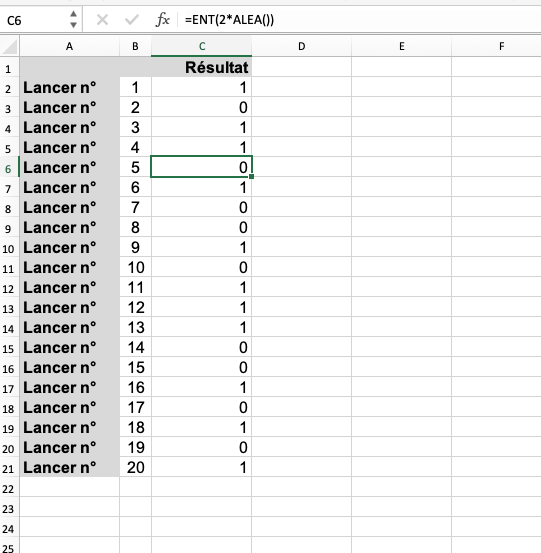
D’autres fonctions du tableur peuvent être utiles.
- La fonction NB.SI(plage;critère) permet de compter le nombres de cellules de la plage qui vérifient un critère donné. Par exemple, =NB.SI(C1:C21;1) compte le nombre de fois ou le 1 est apparu dans les cellules qui vont de C1 à C21. Sur l’exemple ci-dessus, elle répondra 11.
- La fonction SOMME(plage) permet d’additionner tous les nombres sur une plage donnée. Sur l’exemple ci-dessus, =SOMME(C1:C21) additionne tous les nombres contenus dans les cellules C1 jusqu’à C21.
Répéter n fois une expérience de manière indépendante signifie que le résultat d’une répétition n’influence pas le résultat des répétitions suivantes.
Un sac contient 10 boules blanches et 20 boules noires.
Une expérience aléatoire consiste à prendre au hasard une boule dans le sac, à noter « succès » si c’est une boule noire, « échec » sinon, puis à remettre la boule dans le sac.
On répète 8 fois cette expérience. La répétition se fait bien de manière indépendante, car la boule tirée est toujours remise dans le sac, donc le résultat d’un tirage n’influence pas les tirages suivants.
On obtient un échantillon de taille 8 : {succès, échec, échec, succès, succès, échec, succès, succès}.
Reprenons le sac de boules de l’exemple précédent. Si maintenant, à chaque fois que l’on a tiré une boule, on l’enlève du sac, la répétition de cette expérience ne se fera plus de manière indépendante. En effet, si on a enlevé une boule blanche au premier tirage, alors au deuxième tirage on n’aura plus que 9 boules blanches dans le sac (au lieu des 10 qu’il y avait au départ). Le résultat de la 2e expérience dépend donc de celui de la 1re expérience. Dans ce cas, on ne peut pas parler d’échantillon.
On réalise 150 échantillons de 30 lancers d’une pièce équilibrée. On considère comme un « succès » l’issue « obtenir face ».
On obtient le graphique ci-dessous qui représente le nuage de points des fréquences de succès dans chaque échantillon. Chaque point bleu du graphique représente la fréquence de succès dans un seul échantillon.
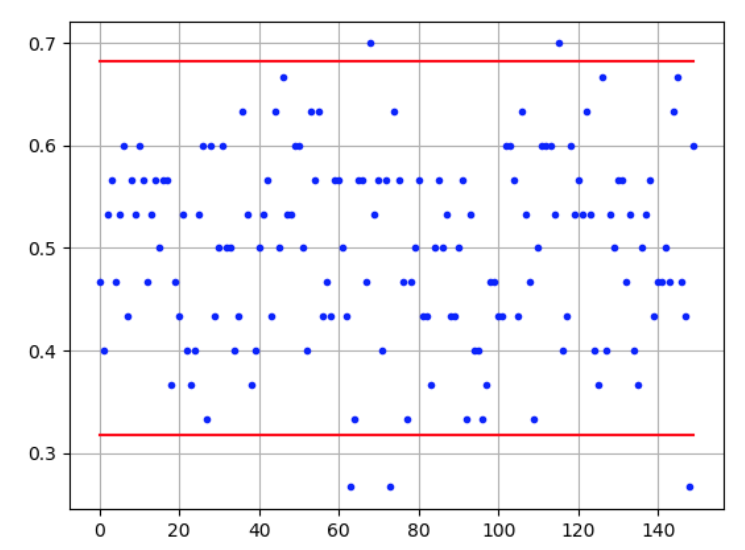
On constate que les fréquences obtenues sont toutes assez différentes les unes des autres (comprises entre 0,25 et 0,7) : on dit qu’il y a fluctuation de l'échantillonnage.
De plus, comme la probabilité d’obtenir un succès pour une pièce équilibrée est de 0,5, théoriquement chacune de ces fréquences devrait être de 0,5.
On réalise 150 échantillons de 1000 lancers de la pièce équilibrée. On constate sur le graphique ci-dessous que le nuage de points des fréquences de succès s’est resserré : les fréquences obtenues sont comprises entre 0,44 et 0,56, soit une dispersion de 0,12.
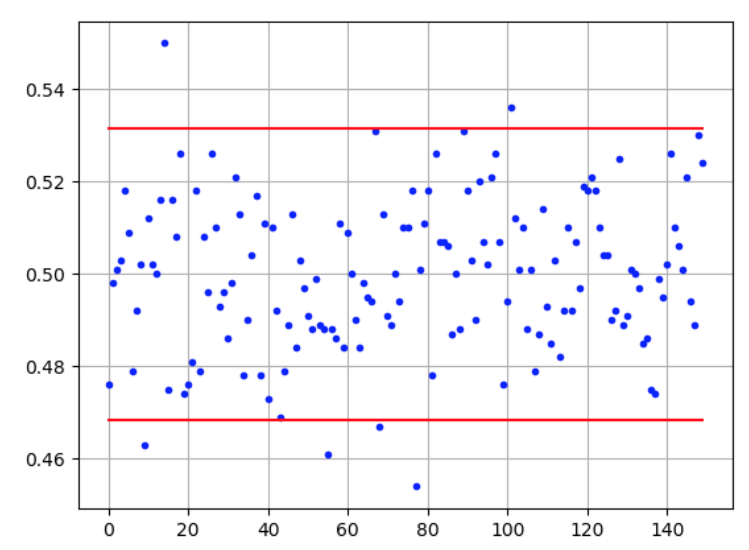
On réalise 150 échantillons de 4000 lancers d’une pièce. On constate sur le graphique ci-dessous que le nuage de points des fréquences de succès s’est resserré : les fréquences obtenues sont comprises entre 0,47 et 0,52, soit une dispersion inférieure à 0,06.
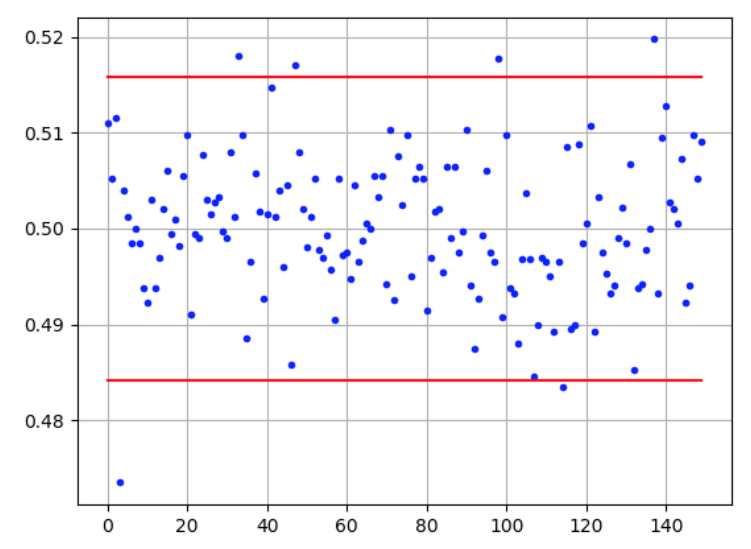
On peut généraliser cette observation par la propriété suivante :
Plus la taille des échantillons est grande, plus l’amplitude des fluctuations diminue.
De plus, entre ces deux simulations, on observe que la dispersion des données à été divisée par 2 alors que la taille des échantillons a été multipliée par 4.
D’où la propriété suivante :
Pour diviser la dispersion des données par k, il faut multiplier la taille des échantillons par k².
On considère :
- N échantillons de taille n des résultats d’une expérience aléatoire à deux issues (« succès » et « échec ») ;
- la série statistique de toutes les fréquences de succès obtenues dans les N échantillons.
On note p la probabilité de succès de chaque expérience ; on note s l’écart type de la série des fréquences de succès.
On souhaite compter le nombre de fréquences de succès situées dans un intervalle de la forme [p – ks ; p + ks] pour k ∈ {1 ; 2 ; 3}.
L’écart type s de la série des fréquences est de l’ordre de
.
Dans l’exemple de la partie 2b montrant le nuage de points des fréquences de succès dans 150 échantillons de 30 lancers d’une pièce équilibrée, p = 0,5 et s =
.
Si on étudie une simulation de N échantillons de taille n :
- En moyenne, environ 68 % des fréquences de succès sont dans l’intervalle [p – s ; p + s] ;
- En moyenne, environ 95 % des fréquences de succès sont dans l’intervalle [p – 2s ; p + 2s] ;
- En moyenne, environ 99 % des fréquences de succès sont dans l’intervalle [p – 3s ; p + 3s].
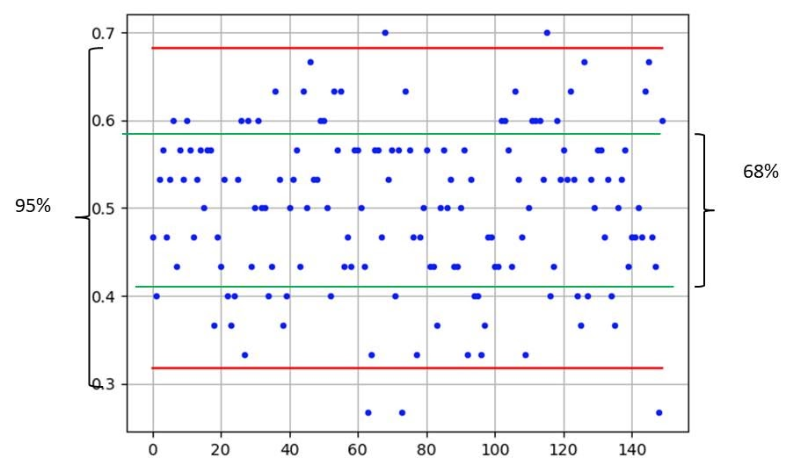
Dans l’exemple de la partie 2b montrant le nuage de points des fréquences de succès dans 150 échantillons de 30 lancers d’une pièce équilibrée, on a p = 0,5 et s = 0,0912. Les fréquences de succès sont réparties de la façon suivante :
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Mathématiques
L'espérance d'une variable aléatoire
Mathématiques
Puissances de 10 et notation scientifique- Première- Mathématiques
Mathématiques
Résoudre une équation comportant un carré
Mathématiques
Convertir des unités de durée
Mathématiques
Convertir des unités de longueur
Mathématiques
Convertir des unités d'aire- Première- Mathématiques
Mathématiques
Convertir des unités de contenance
Mathématiques
Simplification de fractions et fractions irréductibles- Seconde- Mathématiques
Mathématiques
Calculer avec des puissances
Mathématiques
Convertir des unités de grandeur composées
Fermer
Accédez gratuitement à
