Loi binomiale
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Reconnaître un schéma de Bernoulli.
- Calculer des coefficients binomiaux.
- Calculer des probabilités dans le cadre de la loi binomiale.
- Utiliser l’espérance d’une loi binomiale.
- Une épreuve de Bernoulli n'a que 2 issues : un succès S qui se produit avec une probabilité p, un échec S qui se produit avec la probabilité 1-p .
- Un schéma de Bernoulli d’ordre n est la répétition d’une épreuve de Bernoulli n fois où chaque issue est indépendante.
- On nomme coefficient binomial, noté n k et qui se lit : « k parmi n », le nombre de chemins ayant k succès de l’arbre d’un schéma de Bernoulli d’ordre n.
- Un coefficient binomial s'obtient à la calculatrice ou avec un triangle de Pascal.
- Pour un schéma de Bernoulli d’ordre n, de
probabilité p pour chaque succès de
l’épreuve, la loi de probabilité de la
variable X qui à chaque issue associe k
succès est :
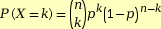avec
0 ≤ k ≤ n. Cette loi s'appelle la loi binomiale de
paramètres n et p et se note B(n,p) .
- L'espérance de B(n,p) est donnée par : E(X)=n p.
- Épreuve de Bernoulli
Cf fiche : Les expériences aléatoires à plusieurs épreuves indépendantes (1ère)
qui se produit avec la
probabilité 1-p.
On lance trois fois de suite une pièce truquée pour laquelle la probabilité d’obtenir pile est
. On gagne 5 € pour chaque
sortie de « Pile ». Tracer
l’arbre pondéré et déterminer
la loi de probabilité de cette variable
aléatoire.Soit X la variable aléatoire qui à chaque issue associe le nombre de succès.
Un succès s est représenté par chaque apparition de l’événement « Pile », de probabilité p =
. L’échec,
l’événement 
aura pour probabilité
.
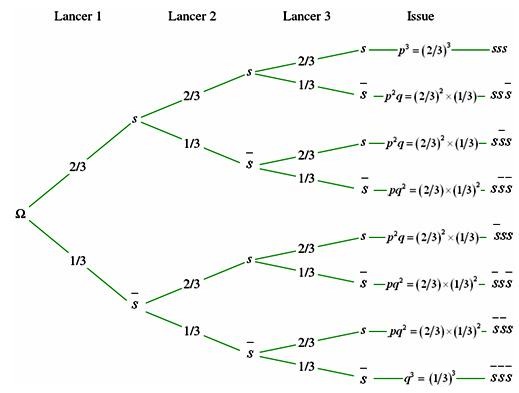
| k | 0 | 1 | 2 | 3 |
| P(X=k) |
|
|
|
|
Les résultats sont laissés sous forme de
fraction de la totalité des cas (on pourrait
passer en fractions irréductibles).
qui se lit k parmi n, le nombre
de chemins ayant k succès de l’arbre
d’un schéma de Bernoulli d’ordre
n.
Pour le schéma de Bernoulli précédent :
- Pour 0 succès on a
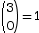car un seul chemin n’a
aucun succès.
- Pour 2 succès on a
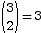car trois chemins ont 2
succès.
Par exemple 
.
- Sur Texas instrument (82 stat, 83 & 84) écrire n (ici 3) puis entrer la fonction « Combinaison » (qui est dans le menu « Math/Prb ») puis l’argument k (ici 2). Si les instructions sont en anglais, la fonction sera « nCr » dans le même menu qu’indiqué.
- Sur TI-NSpire dans une page calcul entrer « nCr(3,2).
-
Sur Casio écrire n (ici 3) puis
entrer la fonction « nCr » (dans «
OPTN » puis « PROB ) puis
l’argument k (ici 2).
Dans une cellule écrire « =COMBIN(3;2)».
avec 
.Notation : cette loi est notée
.
C’est ce que l’on constate avec l’exemple précédent. Pour 2 succès, on peut compter « à la main » la probabilité de chaque chemin et additionner le tout, ce qui donne
. D’après la
définition, pour 
on a 
.
Par exemple P(X=k) pour n = 1000, p = 0,5 et k = 462.
- Sur Texas instrument (82 stat, 83 & 84) entrer la fonction « binomFdp(n,p,k) » (qui est dans le menu « distrib ») avec les arguments n = 1000, p = 0,5 et k = 462.
-
Sur TI-NSpire dans une page calcul entrer
« binomPdf(1000,0.5,462) »
(rappel : les points sont des virgules, les virgules des caractères de séparation des variables). - Sur Casio entrer la fonction « BinomialPD(k,n,p) » (dans « OPTN » puis « STAT » puis « DIST » puis « BINM » et « Bpd » pour finir) avec les arguments k = 462, n = 1000 et p = 0,5.
Dans une cellule écrire « =LOI.BINOMIALE(valeur de k ; n ; p ;FAUX) ».
Par exemple P(X
k) pour n = 1000, p
= 0,5 et k = 462 (utilisé
ci-après).
- sur Texas instrument entrer la fonction « binomFrép(n,p,k) » (qui est dans le menu « distrib ») avec les arguments n = 1000, p = 0,5 et k = 462.
-
sur TI-NSpire dans une page calcul entrer
« binomCdf(1000,0.5,0,462) »
(rappel : les points sont des virgules, les virgules des caractères de séparation des variables). - sur Casio entrer la fonction « BinomialCD(k,n,p) » (dans « OPTN » puis « STAT » puis « DIST » puis « BINM » et « Bcd » pour finir) avec les arguments k = 462 la valeur à tester, n = 1000 et p = 0,5.
Dans une cellule écrire « =LOI.BINOMIALE(valeur de k ; n ; p ;VRAI) » que l’on tirera vers le bas.
On peut remarquer : 
. 
. 
Par convention 
.
- Si
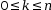alors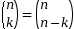 
.
- Si
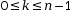alors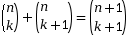 
(formule de Pascal).
Ces deux règles permettent de calculer les coefficients binomiaux de proche en proche, en construisant le « Triangle de Pascal » par exemple.
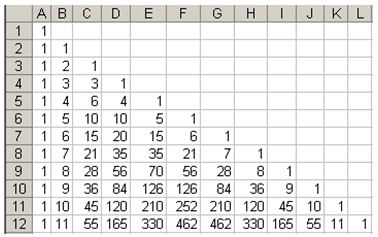
Dans le tableur enlever l’affichage des
zéros (cliquer sur Outils/Options puis
décocher la case « Valeurs zéro
» dans Affichage).
Mettre des 1 en première colonne et en
diagonale.
En B3 écrire une formule du genre « =A2+B2
» que l’on recopie vers le bas. On recopie
aussi cette formule vers la droite pour les cellules sans
valeur à l’intérieur du triangle.
Rappel : les coefficients binomiaux sont obtenus
avec la calculatrice.
-
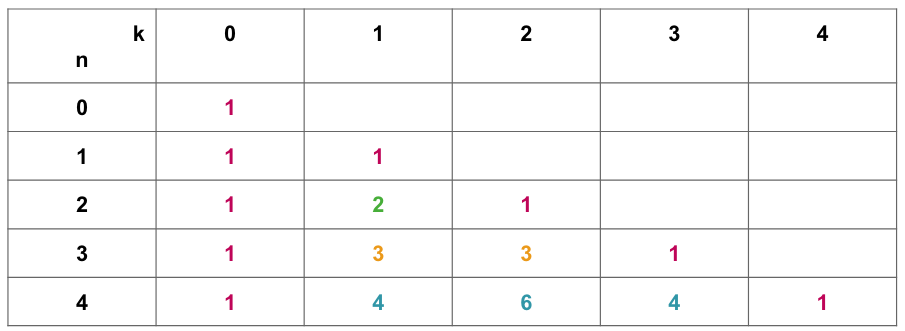
Étape 1 : on remplit la première colonne et la
diagonale à l'aide des formules
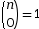et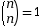 
-
Étape 2 : dans le triangle de
Pascal, chaque case est la somme de la case
située au-dessus, et de celle située
au-dessus à gauche, ainsi on remplit :
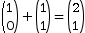
- Étape 3 : on reprend l'étape 2 à la ligne du dessous, et ainsi de suite.
Rappel : les coefficients binomiaux peuvent s'obtiennent aussi avec la calculatrice.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Fermer
Accédez gratuitement à
