Les vecteurs colinéaires et expression d'un vecteur en fonction de 2 vecteurs non colinéaires
et
sont
colinéaires lorsqu’il existe un
réel 
tel
que 
.
, le
vecteur nul est donc colinéaire à tout
autre vecteur.Exemple :
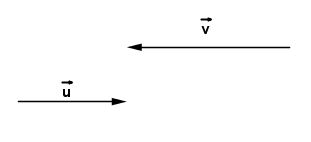
Sur le dessin ci-dessus,
donc
et
sont
colinéaires.Conséquences géométriques :
Dire que les vecteurs
et
sont
colinéaires signifie que les points A,
B, C sont alignés.Dire que les vecteurs non nuls
et
sont
colinéaires signifie que les droites
(AB) et (CD) sont
parallèles.
du plan,
dire que les vecteurs 
et
sont
colinéaires signifie que 
.Preuve :
Dire que les vecteurs
et
sont
colinéaires signifie que 
.En classe de seconde, on a vu que
a pour
coordonnées 
.Ainsi dire que
signifie
que 
et
,
autrement dit les coordonnées de 
et
sont
proportionnelles.Ainsi, le tableau suivant est un tableau de proportionnalité :
| x | x' |
| y | y' |
et les produits xy' et x'y sont égaux, d'où le résultat
soit
.est un
repère du plan.Les points
,
,
sont-ils
alignés ?
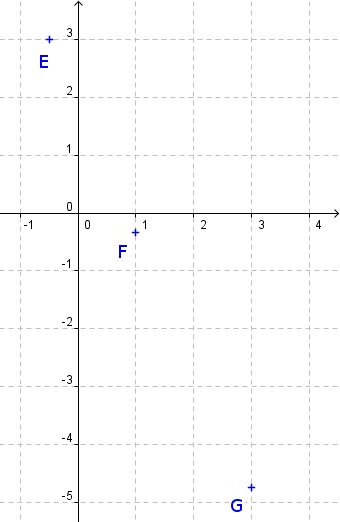
Dire que les points E, F et G sont alignés revient à dire que les vecteurs
et
sont
colinéaires : 
soit
.De même
soit
.
donc les vecteurs
et
ne sont
pas colinéaires d’où E,
F, G, ne sont pas alignés.
et
deux
vecteurs non colinéaires du plan.Pour tout vecteur
il
existe un couple unique (x, y) de réels tels
que 
.
Autrement dit, tout vecteur
se
décompose d'une façon unique en fonction
de
et
.
et
.1°) Prouver que les vecteurs
et
ne sont
pas colinéaires.2°) Exprimer le vecteur
en
fonction des vecteurs 
et
.1°) On peut calculer le réel xy' – x'y et montrer qu’il est non nul ; on peut aussi lire directement que les coordonnées des 2 vecteurs ne sont pas proportionnelles :
en effet,
et
2°) D’après la propriété ci-dessus, il existe 2 réels uniques x et y tels que
Le vecteur
a pour
coordonnées 
Dire que le vecteur
est
égal au vecteur 
signifie
que leur coordonnées sont égales.À savoir
Nous pouvons conclure que
et
sont
colinéaires revient à dire que
.
et
étant
2 vecteurs non colinéaires, tout vecteur 
s’écrit
de façon unique 
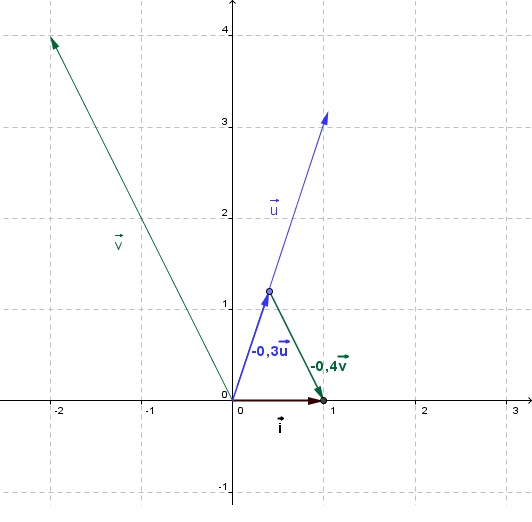
où x et y sont 2 réels.
Vous avez déjà mis une note à ce cours.
Découvrez les autres cours offerts par Maxicours !
Découvrez MaxicoursComment as-tu trouvé ce cours ?
Évalue ce cours !
Teste dès maintenant tes nouvelles connaissances dans notre quiz
Quiz sur le cours ‘Les vecteurs colinéaires et expression d’un vecteur en fonction de 2 vecteurs non colinéaires’ – mathématiques
Réussis ton année de première générale avec le soutien scolaire en ligne Maxicours ! Teste tes connaissances avec notre quiz de mathématiques sur le cours intitulé ‘Les vecteurs colinéaires et expression d’un vecteur en fonction de 2 vecteurs non colinéaires’. Réponds à l’ensemble des questions et vérifie ton taux de bonnes réponses. Tu peux même recevoir par e-mail les réponses détaillées avec les rappels de cours en nous laissant ton adresse !
Fiches de cours les plus recherchées
Découvrir le reste du programme
Des profs en ligne
- 6 j/7 de 17 h à 20 h
- Par chat, audio, vidéo
- Sur les matières principales
Des ressources riches
- Fiches, vidéos de cours
- Exercices & corrigés
- Modules de révisions Bac et Brevet
Des outils ludiques
- Coach virtuel
- Quiz interactifs
- Planning de révision
Des tableaux de bord
- Suivi de la progression
- Score d’assiduité
- Un compte Parent
Message envoyé
