Les représentations graphiques d'une série statistique- Terminale- Mathématiques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Identifier, construire et lire un diagramme en bâtons.
- Identifier, construire et lire un histogramme.
- Identifier, construire et lire un diagramme circulaire.
- Identifier, construire et lire un polygone des effectifs.
- Identifier, construire et lire un diagramme en boite.
- Une série statistique peut être
représentée de différentes
façons : sous forme de liste, de tableau, de
graphique, etc.
La représentation graphique d’une série statistique peut faciliter son étude et permettre de comparer plusieurs séries plus rapidement. - Il existe différents types de représentations graphiques d’une série statistique : diagramme en bâtons, histogramme, diagramme circulaire, polygone des effectifs, diagramme en boite... Le choix d’une représentation dépend du type de série et du message que l’on veut faire passer.
- Construire un angle au rapporteur
- Vocabulaire des séries statistiques
- Médiane, quartiles, valeur minimale et valeur maximale d'une série statistique
Une série statistique peut être
représentée de différentes façons
: sous forme de liste, de tableau, de graphique, etc.
La représentation graphique d’une série
statistique peut faciliter son étude et permettre de
comparer plusieurs séries plus rapidement.
Il existe différents types de représentations graphiques d’une série statistique. Le choix d’une représentation dépend du type de série et du message que l’on veut faire passer.
Il est très utilisé pour représenter des effectifs ou des fréquences.
On met généralement le caractère étudié en abscisse et les effectifs correspondants en ordonnée. Il faut bien choisir les unités pour que le diagramme soit le plus lisible possible.
On a interrogé 100 personnes sur la question suivante : « Combien de fois avez-vous été au cinéma le mois dernier ? »
Les réponses ont été rassemblées dans le tableau ci-dessous.
| Nombre de séances | 0 | 1 | 2 | 3 | 4 |
| Effectif | 18 | 30 | 22 | 19 | 11 |
Sur l’axe des ordonnées, on peut choisir 4 cm pour 10 personnes.
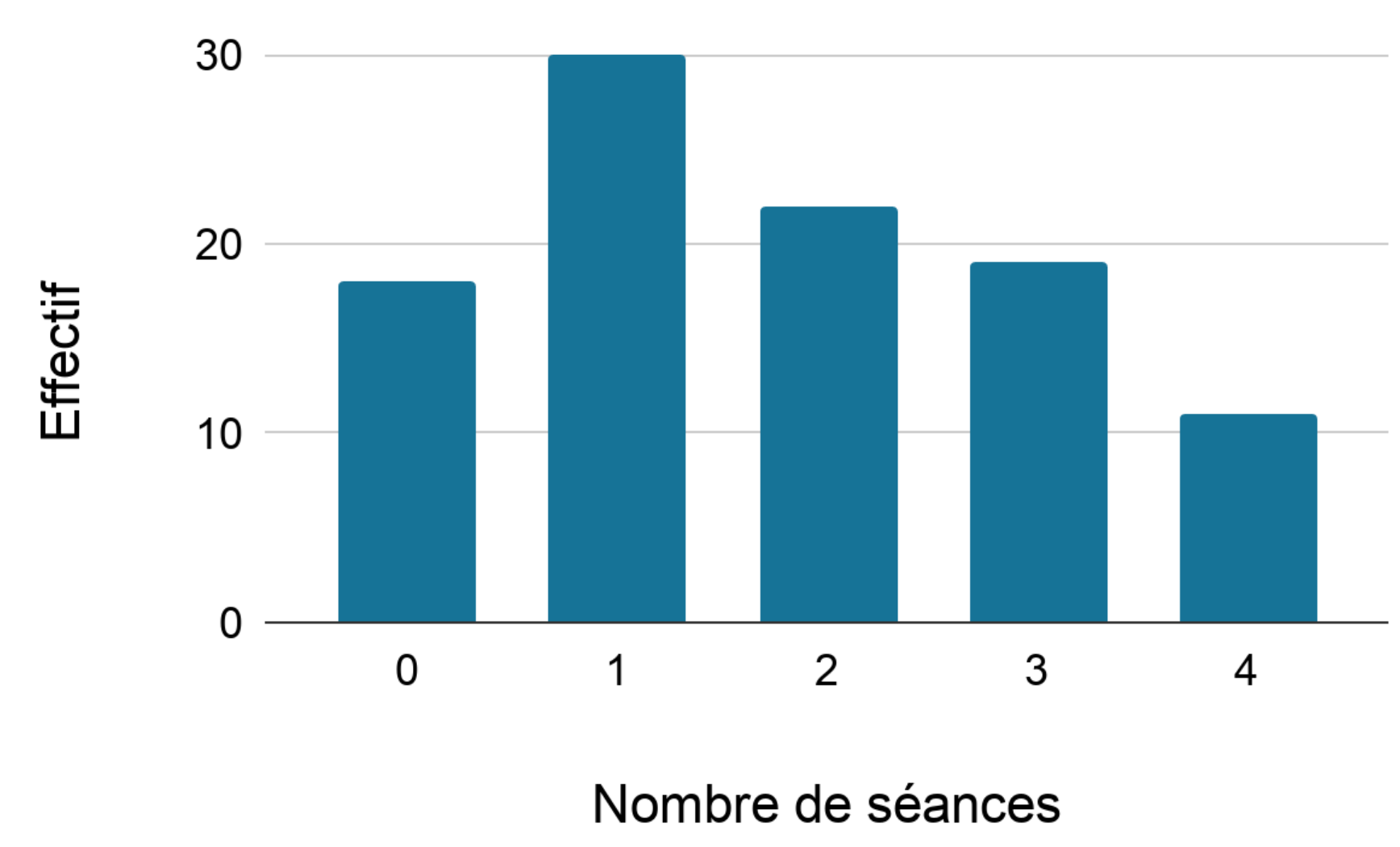
On obtient le diagramme en bâtons suivant.
 Répartition des
effectifs en fonction du nombre de séances de
cinéma
Répartition des
effectifs en fonction du nombre de séances de
cinéma
Généralement, le caractère
étudié est en abscisse et l'effectif
correspondant en ordonnée. Dans ce cas, la hauteur
de chaque barre est proportionnelle à
l'effectif.
Si le caractère étudié est en
ordonnée et l'effectif en abscisse, c'est la
longueur de chaque barre (de gauche à droite) qui
est proportionnelle à l'effectif.
Dans le diagramme en bâtons ci-dessus, le caractère étudié est le nombre de séances de cinéma (en abscisse) et l'effectif correspondant est en ordonnée.
La deuxième barre verticale en partant de la gauche signifie que 30 personnes ont été au cinéma une seule fois le mois dernier.
Il est très utilisé pour représenter les effectifs ou les fréquences de ces classes.
On met généralement le caractère étudié en abscisse et les effectifs correspondants en ordonnée. Il faut bien choisir les unités pour que le diagramme soit le plus lisible possible.
Dans une entreprise, pour être vendues, les pommes de terre sont triées selon leur calibre. On a regroupé les résultats dans le tableau suivant.
| Calibre en mm | [60 ; 65[ | [65 ; 70[ | [70 ; 75[ | [75 ; 80[ |
| Quantité en kg | 105 | 156 | 145 | 98 |
Sur l’axe des ordonnées, on peut choisir 1 cm pour 10 kg.
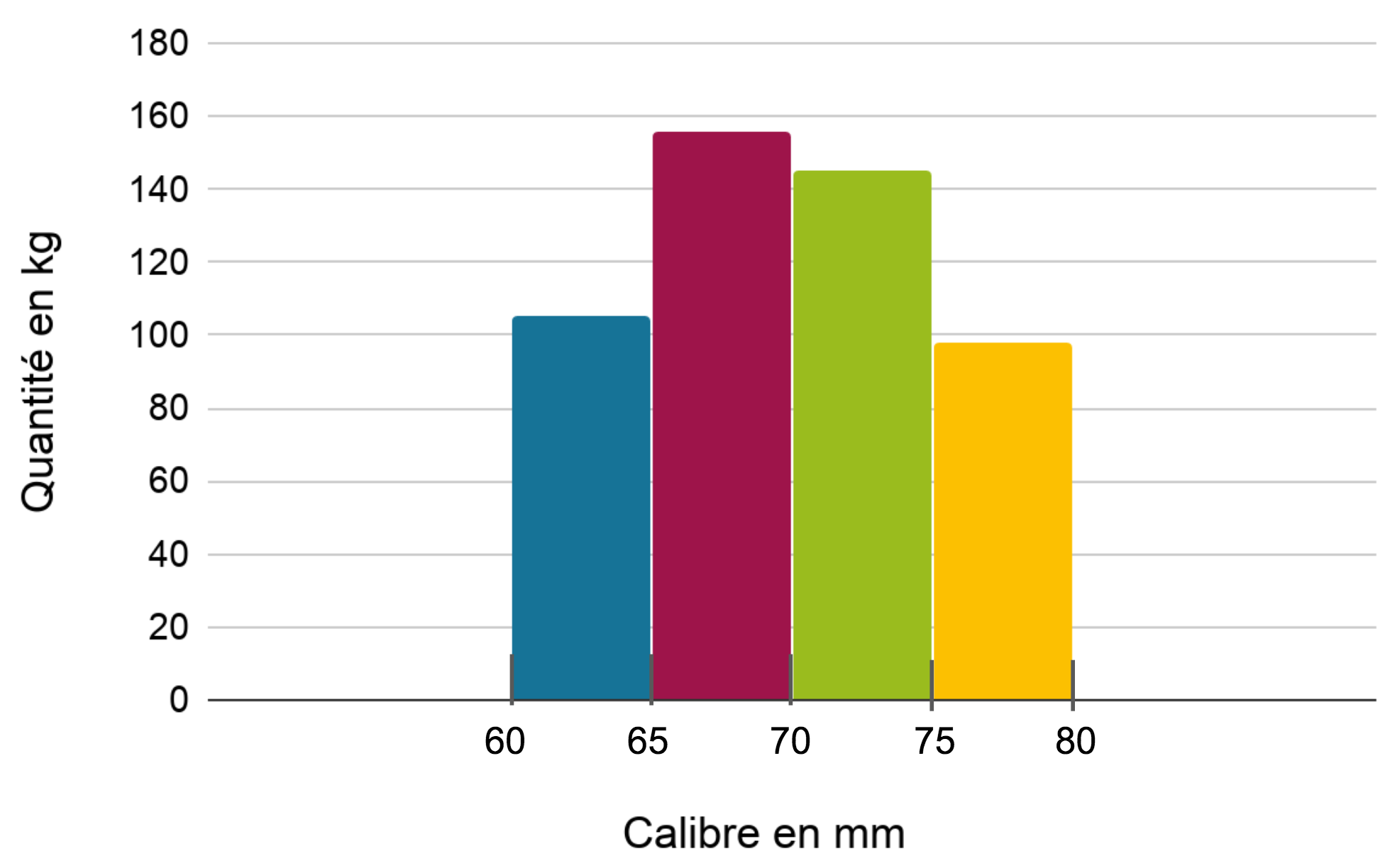
On obtient l’histogramme correspondant.
 Répartition de la
quantité de pommes de terre en fonction de leur
calibre
Répartition de la
quantité de pommes de terre en fonction de leur
calibre
Généralement, le caractère
étudié est en abscisse et l'effectif
correspondant en ordonnée. Dans ce cas, la hauteur
de chaque barre est proportionnelle à
l'effectif.
Si le caractère étudié est en
ordonnée et l'effectif en abscisse, c'est la
longueur de chaque barre (de gauche à droite) qui
est proportionnelle à l'effectif.
Dans l'histogramme ci-dessus, le caractère étudié est le calibre de pommes de terre (en abscisse) et l'effectif correspondant est en ordonnée.
La barre verte signifie qu'environ 145 kg de pommes de terre ont un calibre compris entre 70 et 75 mm.
Un diagramme circulaire entier mesure 360°.
- calculer les angles associés à chacune
des valeurs du caractère étudié.
Pour cela, utiliser la formule :
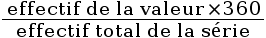 ;
;
- dessiner un cercle ;
- placer un premier rayon ;
- construire les angles les uns à la suite des autres.
On reprend l’exemple précédent du calibre des pommes de terre.
| Calibre en mm | [60 ; 65[ | [65 ; 70[ | [70 ; 75[ | [75 ; 80[ |
| Quantité en kg | 105 | 156 | 145 | 98 |
| Angle en degrés |
|
|
|
|
 Répartition des
quantités de pommes de terre en fonction de leur
calibre
Répartition des
quantités de pommes de terre en fonction de leur
calibre
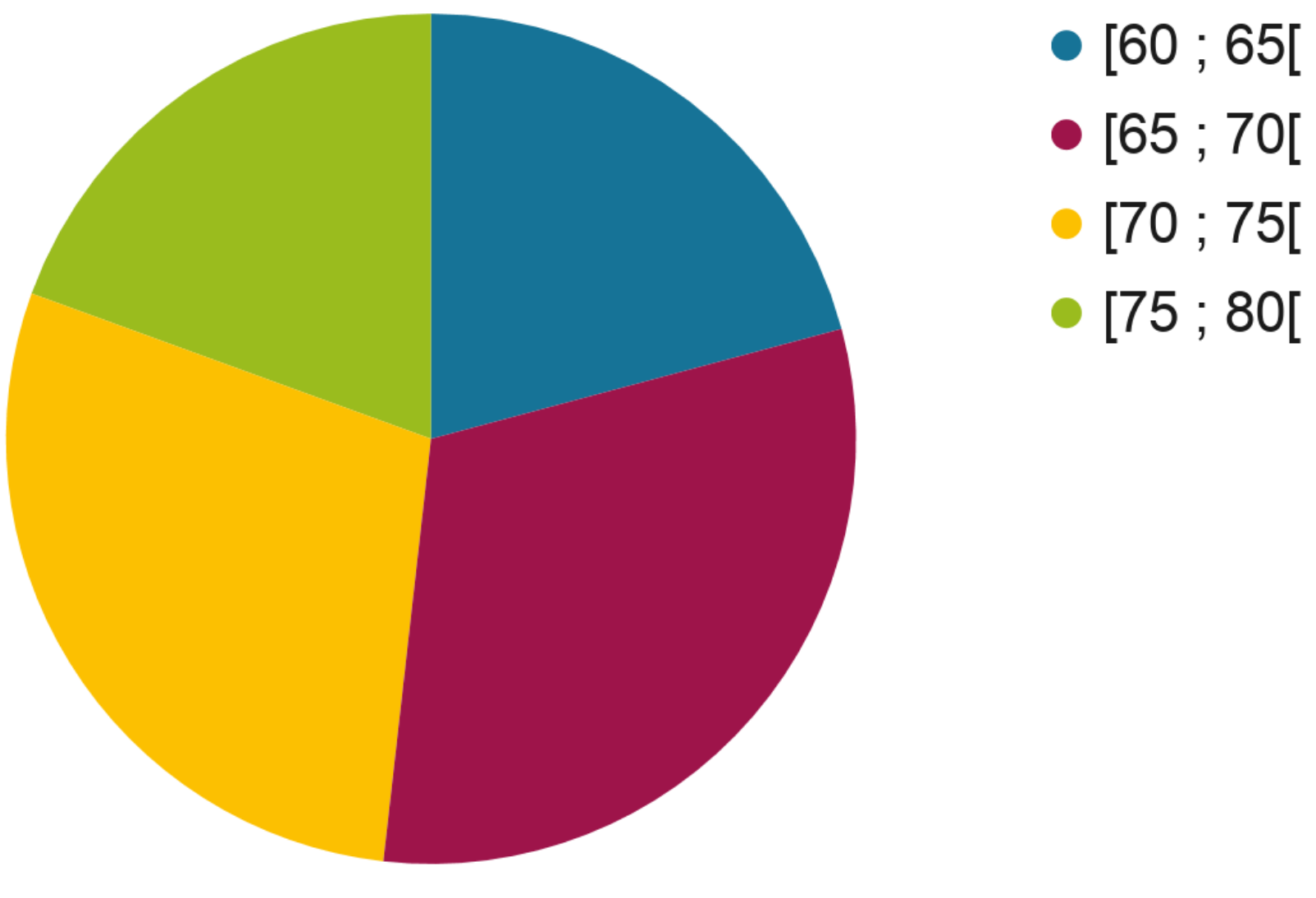
Chaque secteur correspond à une valeur du caractère étudié. L'angle de chaque secteur est proportionnelle à l'effectif de la valeur : plus l'angle est grand, plus l'effectif est important.
Dans le diagramme circulaire ci-dessus, le caractère étudié est le calibre de pommes de terre. Chaque secteur indique une valeur différente de ce calibre. Il y a quatre secteurs de couleurs différentes, donc quatre valeurs différentes de calibre en mm :
Le secteur jaune signifie qu'un peu plus d'un quart de la quantité totale de pommes de terre a un calibre compris entre 70 et 75 mm.
- réfléchir au choix des unités avant de commencer pour que toutes les valeurs soient représentées ;
- en général, mettre le caractère étudié en abscisse et les effectifs correspondants en ordonnée ;
- placer les points du tableau dans le repère et les relier par des segments.
À l’occasion d’une épreuve de saut en hauteur, on a noté les résultats des participants dans le tableau ci-dessous.
| Hauteur en cm | 105 | 110 | 115 | 120 | 125 |
| Effectif | 4 | 3 | 12 | 4 | 5 |
Sur l’axe des ordonnées, on peut choisir 1 cm pour 1 élève.
On obtient le polygone des effectifs correspondant.
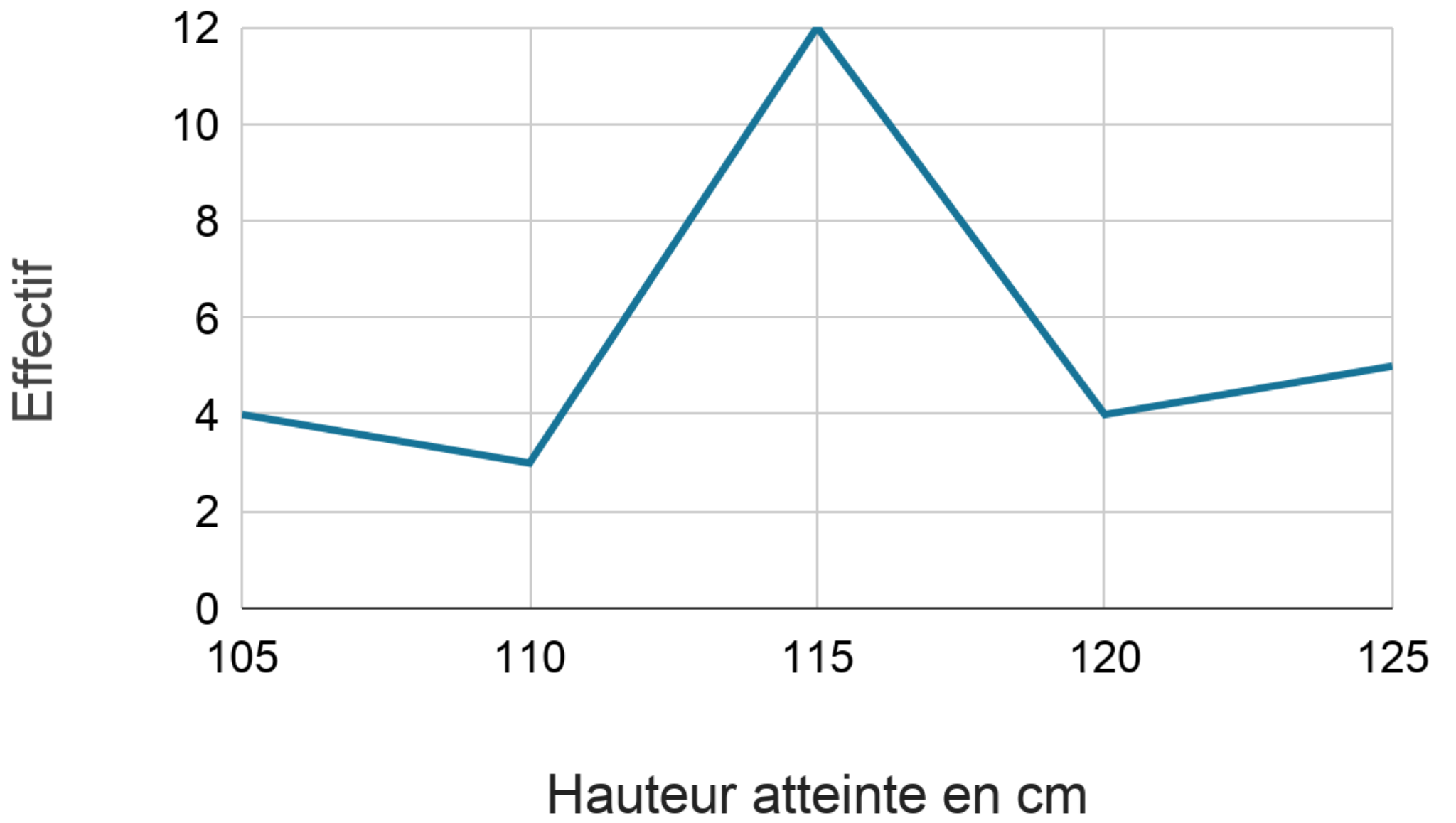 Répartition des
effectifs en fonction de la hauteur atteinte
Répartition des
effectifs en fonction de la hauteur atteinte
Si on reprend l’exemple précédent et qu’on le complète avec les fréquences cumulées croissantes, on obtient :
| Hauteur en cm | 105 | 110 | 115 | 120 | 125 |
| Effectif | 4 | 3 | 12 | 4 | 5 |
| Fréquence cumulée |
|
|
|
|
1 |
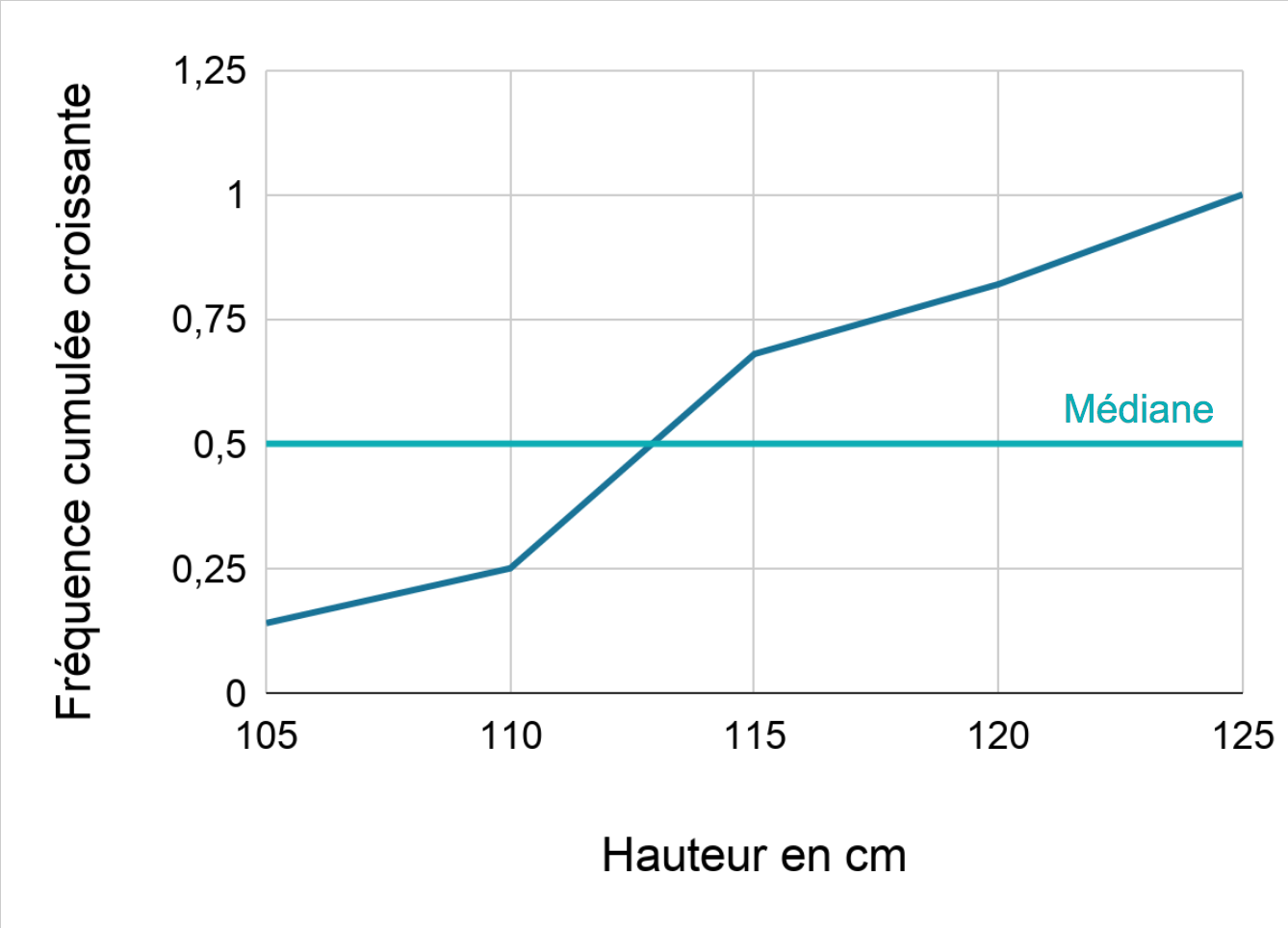
Fréquence cumulée croissante de la hauteur atteinte
Par lecture graphique, on trouve une médiane de 113.
Dans le cas d'un polygone des effectifs simple, le
caractère étudié est
généralement en abscisse et l'effectif
correspondant en ordonnée.
Dans le cas d'un polygone des fréquences
cumulées croissantes, le caractère
étudié est généralement en
abscisse et la fréquence cumulée croissante
en ordonnée. La médiane est la valeur en
abscisse pour laquelle la fréquence cumulée
croissante vaut 0,5.
Dans le graphique des fréquences cumulées croissantes ci-dessus, le caractère étudié est la hauteur atteinte en cm (en abscisse) et la fréquence cumulée croissante est en ordonnée.
On lit que 75 % des participants ont atteint une hauteur comprise entre 105 et 118 cm environ.
Pour connaitre la valeur médiane, on trace une droite horizontale d'équation y = 0,5 et on lit la valeur de l'abscisse du point d'intersection entre la droite et le polygone. On trouve une hauteur médiane de 113 cm.
- la médiane Me ;
- les quartiles Q1 et Q3 ;
- les minimales et maximales du caractère (Min et Max).
Il est possible d'y trouver également les déciles D1 et D9 (et même des centiles...).
Il se construit de la manière suivante :

En réalité, sur l'axe gradué qui est
sous la boite ne doivent figurer que les valeurs des
graduations.
Le diagramme en boite permet de visualiser les quatre
quarts de la série :
- 25 % de la population a une valeur de caractère
inférieure à Q1 ;
- 50 % de la population a une valeur de caractère
inférieure à Me ;
- 75 % de la population a une valeur de caractère
inférieure à Q3 ;
- 100 % de la population a une valeur de caractère
inférieure à Max.
Le diagramme indique aussi l'étendue de la
série (la longueur du diagramme) et l'écart
interquartile (la longueur de la boite).
On a ainsi 50 % de la population « dans la
boite ».
On considère la série statistique de 50 valeurs présentées dans le tableau ci-dessous. On a pris soin de les ordonner de la plus petite à la plus grande.
|
5 |
15 |
19 |
21 |
29 |
|
7 |
16 |
19 |
21 |
30 |
|
11 |
16 |
19 |
23 |
33 |
|
14 |
16 |
19 |
24 |
33 |
|
15 |
16 |
19 |
24 |
33 |
|
15 |
16 |
20 |
25 |
33 |
|
15 |
16 |
20 |
25 |
33 |
|
15 |
17 |
20 |
26 |
34 |
|
15 |
18 |
20 |
27 |
34 |
|
15 |
18 |
21 |
28 |
35 |
La plus petite valeur est Min = 5, la plus grande Max =
35.
Il y a 50 valeurs, la médiane est la moyenne de
la 25e et de la 26e :
Me = (19 + 20) ÷ 2 = 19,5.
Pour Q1 : 25 % de 50, cela fait 12,5. Il
faut laisser au moins 25 % en dessous de Q1,
on prend la 13e valeur : Q1 =
16.
Pour Q3 : 75 % de 50, cela fait 37,5. Il
faut laisser 75 % au moins en dessous de Q3,
on prend la 38e valeur: Q3 =
26.
L'écart interquartile est donc égal
à Q3
– Q1 = 26 – 16 =
10.
Voici une représentation de la boite à
moustache de cette série.


Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









