Les listes en Python : application aux probabilités et statistiques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Dans le cadre des statistiques et des probabilités :
- Définir une liste en Python par extension et par compréhension.
- Manipuler les éléments d’une liste (ajout, suppression, modification).
- Parcourir les éléments d’une liste.
- Itérer sur les éléments d’une liste.
- On peut simuler avec Python une expérience
aléatoire, par exemple celle qui consiste à
lancer un dé équilibré un certain
nombre de fois n. Pour obtenir les
résultats de cette expérience, on a besoin de
deux fonctions :
- la première pour simuler le lancer du dé ;
- la seconde pour construire la liste des résultats, c’est-à-dire la liste de toutes les faces obtenues à l’issue des n lancers du dé.
- On peut également analyser des données
statistiques, par exemple des données
météorologiques. Dans une ville, on
relève chaque jour la température pendant une
période de 30 jours. Pour déterminer la
température maximale, la température minimale
et la température moyenne sur 30 jours, on a
besoin de 3 fonctions :
- une fonction max_val qui retourne la valeur maximale de la liste ;
- une fonction min_val qui retourne la valeur minimale ;
- une fonction moyenne_val qui retourne la valeur moyenne.
- On peut définir une fonction qui calcule l’espérance d’une variable aléatoire.
- Il est possible de comparer l’espérance d’une loi de probabilité et la valeur moyenne d’un échantillon de taille n. On peut ainsi vérifier que lorsque la taille n de l’échantillon est importante, la valeur de la moyenne de l’échantillon se rapproche de la valeur de l’espérance.
- Connaitre la notion de variable en Python
- Savoir utiliser des instructions conditionnelles et des boucles
- Connaitre la notion de fonction en Python
Les listes en Python peuvent être utilisées dans de nombreuses parties du programme. Cette fiche présente quelques utilisations possibles.
On considère un dé à six faces parfaitement équilibrées et numérotées de 1 à 6. On s’intéresse à l’expérience aléatoire consistant à lancer ce dé un certain nombre de fois n.
Pour obtenir plus facilement les résultats de
cette expérience, on la simule à
l’aide d’un programme en Python.
Pour cela, on réfléchit d’abord
à l’algorithme à mettre en place.
Il peut s’écrire sous la forme suivante.
tirer le dé
ajouter le résultat obtenu aux résultats
Retourner les résultats
Pour obtenir les résultats de cette expérience aléatoire, on a donc besoin de deux fonctions en Python :
- la première pour simuler le lancer du dé ;
- la seconde pour construire la liste des résultats, c’est-à-dire la liste de toutes les faces obtenues à l’issue des n lancers du dé.
Pour simuler le lancer d’un dé à six faces, on rédige le programme suivant :
| Langage Python | Interprétation |
|
L1 from random import* L2 def de(): L3 return randint(1, 6) |
L1 : On importe le module random. L2 : On définit la fonction de() pour simuler le lancer de dé. L3 : La commande randint(1,6) tire un nombre entier aléatoire compris entre 1 et 6 inclus. La commande return retourne le nombre entier obtenu. |
Une fois la fonction exécutée, on obtient, par exemple, les résultats suivants :
L1 de() # On
appelle la fonction de() qui simule le lancer
d’un dé à six faces.
L2 3 # On
obtient le résultat 3.
L3 de() # On
appelle la fonction de() qui simule le lancer
d’un dé à six faces.
L4 1 # On
obtient le résultat 1.
Pour construire la liste des résultats, c’est-à-dire la liste de toutes les faces obtenues à l’issue des n lancers du dé, on rédige le programme suivant :
| Langage Python | Interprétation |
|
L1 def
tirages(n): L2 liste_tirages=[] L3 while len(liste_tirages)<n: L4 liste_tirages.append(de()) L5 return liste_tirages |
L1 : On définit la fonction tirages(n) qui crée
une liste contenant n résultats. L2 : On déclare les tirages comme une liste vide. L3, L4 : La boucle while ajoute un tirage de dé à la liste tant que la longueur de la liste est inférieure à n. L5 : La commande return retourne la liste des tirages. |
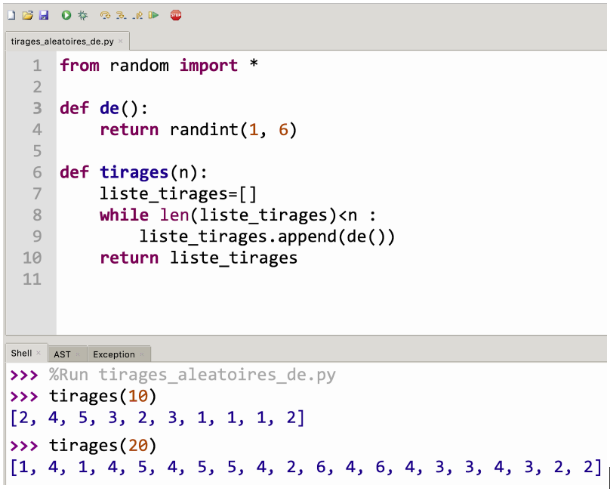
Les deux fonctions précédentes ayant été exécutées, on obtient par exemple les résultats suivants :
L1 tirages(10) # On
appelle la fonction tirages(10) qui simule 10 fois le
lancer d’un dé à six faces.
L2 [4, 3, 4, 5, 2, 1, 6, 4,
6, 3] # On obtient une liste de
10 résultats.
L3 tirages(20) # On
appelle la fonction tirages(10) qui simule
20 fois le lancer d’un dé à
six faces.
L4 [1, 3, 3, 2, 2, 4, 2, 5,
1, 1, 5, 5, 1, 1, 1, 5, 3, 2, 1, 5] # On obtient
une liste de 20 résultats.
Le programme final est donc :
L2 def de():
L3 return randint(1, 6)
L4 def tirages(n):
L5 liste_tirages=[]
L6 while len(liste_tirages)<n:
L7 liste_tirages.append(de())
L8 return liste_tirages
Dans une ville, on relève chaque jour la température pendant une période de 30 jours. Ces données sont indiquées sous la forme d’une liste de 30 valeurs, exprimées en degrés Celsius.
Pour analyser ces données, on veut
déterminer la température maximale, la
température minimale et la température
moyenne sur 30 jours.
On a donc besoin de 3 fonctions :
- une fonction max_val qui retourne la valeur maximale de la liste ;
- une fonction min_val qui retourne la valeur minimale ;
- une fonction moyenne_val qui retourne la valeur moyenne.
Il existe déjà une fonction implémentée en Python qui retourne la valeur maximale d’une liste. Elle se nomme tout simplement max.
def
max_val(liste): # fonction qui retourne la
valeur maximale d’une liste
return
max(liste)
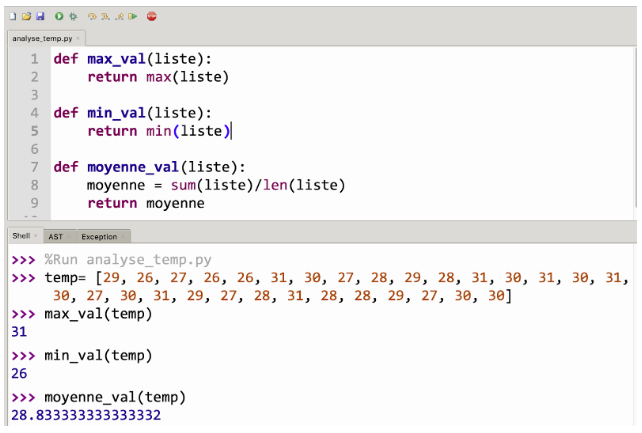
Si les températures relevées sont contenues dans une liste temp et que la fonction max_val a été exécutée, on obtient :
| Langage Python | Interprétation |
|
L1 temp= [29, 26, 27,
26, 26, 31, 30, 27, 28, 29, 28, 31, 30, 31, 30,
31, 30, 27, 30, 31, 29, 27, 28, 31, 28, 28, 29,
27, 30, 30] L2 max_val(temp) L3 31 |
L1 : On définit la liste temp qui contient les
30 températures relevées. L2 : On appelle la fonction max_val. L3 : La valeur maximale retournée est 31. |
La fonction min implémentée en Python retourne la valeur minimale d’une liste.
def
min_val(liste): # fonction qui retourne la
valeur minimale d’une liste
return
min(liste)
Si les températures relevées sont contenues dans une liste temp et que la fonction min_val a été exécutée, on obtient :
| Langage Python | Interprétation |
|
L1 temp= [29, 26, 27,
26, 26, 31, 30, 27, 28, 29, 28, 31, 30, 31, 30,
31, 30, 27, 30, 31, 29, 27, 28, 31, 28, 28, 29,
27, 30, 30] L2 min_val(temp) L3 26 |
L1 : On définit la liste temp qui contient les
30 températures relevées. L2 : On appelle la fonction min_val. L3 : La valeur minimale retournée est 26. |
Pour calculer la moyenne d’une liste, il suffit de calculer la somme de toutes les valeurs puis de la diviser par l’effectif total.
- La fonction sum() permet de calculer la somme des éléments d’une liste ne comportant que des valeurs numériques.
- L’effectif total est déterminé par le nombre total de valeurs de la liste, ce qui correspond à la longueur de la liste.
On a donc :
L2 moyenne = sum(liste)/len(liste)
L3 return moyenne
On obtient :
| Langage Python | Interprétation |
|
L1 temp= [29, 26, 27,
26, 26, 31, 30, 27, 28, 29, 28, 31, 30, 31, 30,
31, 30, 27, 30, 31, 29, 27, 28, 31, 28, 28, 29,
27, 30, 30] L2 moyenne_val(temp) L3 28.833333333333332 |
L1 : On définit la liste temp qui contient les
30 températures relevées. L2 : On appelle la fonction moyenne_val. L3 : La valeur moyenne retournée est 28,833333333333332. |
On considère un dé parfaitement
équilibré à six faces,
numérotées de 1 à 6.
On note X le
résultat obtenu après un lancer de
dé.
X est alors une variable aléatoire discrète : X ne peut prendre qu’un nombre fini de valeurs appartenant à {1, 2, 3, 4, 5, 6} mais on ne peut déterminer exactement quelle sera cette valeur.
À chaque valeur xi ∈ {1,2,3,4,5,6}, on peut
associer la probabilité pi =
p(X = xi).
Comme on est ici en situation
d’équiprobabilité, toutes les
probabilités sont égales
à ![]() .
.
On appelle espérance de la variable
aléatoire X, le nombre défini
par : ![]() .
.
L’espérance d’une variable aléatoire dépend des valeurs possibles de X et des probabilités associées, c’est-à-dire de la loi de probabilité de X.
On peut utiliser une liste de listes en Python pour
décrire la loi de probabilité d’une
variable aléatoire.
Si l’on revient à notre exemple du
dé et si l’on note loi_X la loi de probabilité
associée à X, on a :
loi_X=[[1,1/6],[2,1/6],[3,1/6],[4,1/6],[5,1/6],[6,1/6]]
Cette liste contient 6 éléments
entre crochets.
Chacun des éléments entre crochets est
une liste à 2 éléments
correspondant aux valeurs possibles
de X et
à leur probabilité.
Le premier élément de la liste [1, 1/6]
signifie que X peut prendre la
valeur 1 avec une probabilité
de ![]() .
.
On peut alors accéder aux différents éléments de la liste à l’aide des indices :
- accès au premier élément de la
liste loi_X
>>> loi_X[0]
[1, 0.16666666666666666] - accès au premier élément du
premier élément de la liste
>>>loi_X[0][0]
1 - accès au second élément du
premier élément de la liste
>>>loi_X[0][1]
0.16666666666666666
L’algorithme permettant de calculer l’espérance d’une variable aléatoire X est :
On calcule le produit xi × pi
On l’ajoute à l’espérance
On retourne l’espérance
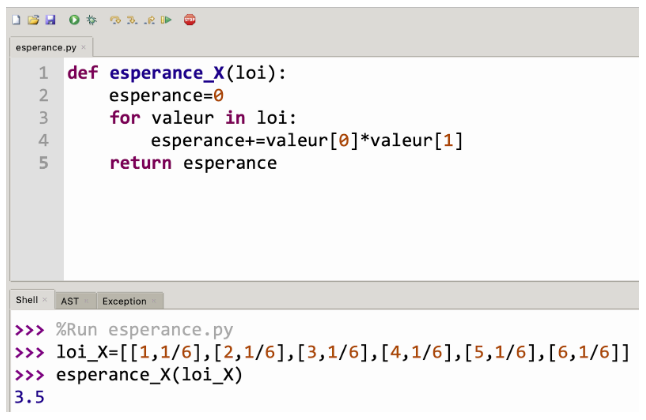
On a donc le programme suivant en Python :
| Langage Python | Interprétation |
|
L1 def
esperance_X(loi): L2 esperance=0 L3 for valeur in loi: L4 esperance+=valeur[0]*valeur[1] L5 return esperance |
L1 : On définit la fonction esperance_X qui calcule
l’espérance de X à partir de sa
loi de probabilité. L2 : On déclare que l’espérance vaut 0. L3, L4 : La boucle for calcule la somme des produits du premier terme par le second terme pour chaque élément de la liste loi. L5 : La commande return retourne l’espérance ainsi calculée. |
Après exécution, on obtient :
L2 esperance_X(loi_X)
L3 3.5
Si on veut vérifier pour la
variable X, on
a bien :
![]()
![]()
En raison de la difficulté à coder des nombres décimaux (ou flottants) en Python, on peut obtenir des résultats numériques non exacts. Pour améliorer la précision, on peut alors avoir recours à des modules spécifiques ou travailler avec des valeurs exactes.
Il existe un lien entre la notion
d’espérance en probabilité et la
notion de moyenne en statistiques.
Pour le mettre en évidence, nous allons
étudier la distance entre
l’espérance d’une loi de
probabilité et la valeur moyenne d’un
échantillon de taille n.
Pour cela, nous allons reprendre l’exemple du
lancer de dé et les fonctions définies
précédemment.
Nous allons avoir besoin :
- de la fonction simulant un échantillon de n lancers (voir la partie 1 de la fiche, Simulation d’une expérience aléatoire) ;
- de la fonction calculant la moyenne d’une série statistique (voir la partie 2 de la fiche, Analyse de données statistiques) ;
- de la fonction déterminant l’espérance d’une variable aléatoire connaissant sa loi de probabilité (voir la partie 3 de la fiche, Calcul de l’espérance d’une variable aléatoire) ;
- d’une nouvelle fonction ecart_moyenne_esperance qui calculera la distance entre la moyenne et l’espérance.
Il suffit donc de reprendre certaines fonctions définies précédemment :
| Langage Python | Interprétation |
|
L1 from random
import* L2 def de(): L3 return randint(1, 6) L4 def tirages(n): L5 liste_tirages=[] L6 while len(liste_tirages)<n: L7 liste_tirages.append(de()) L8 return liste_tirages L9 def moyenne_val(liste): L10 moyenne = sum(liste)/len(liste) L11 return moyenne L12 def esperance_X(loi): L13 esperance=0 L14 for valeur in loi: L15 esperance+=valeur[0]*valeur[1] L16 return esperance |
L1 à L3 : On exécute la fonction
de() pour
simuler le lancer d’un dé à
six faces. L4 à L8 : On exécute la fonction tirages(n) qui construit la liste de résultats des n lancers de dé. L9 à L11 : On exécute la fonction moyenne_val qui calcule la valeur moyenne de la liste. L12 à L16 : On exécute la fonction esperance_X qui calcule l’espérance de la variable aléatoire X. |
Puis, on ajoute la fonction ecart_moyenne_esperance au programme précédent :
| Langage Python | Interprétation |
|
L17 def
ecart_moyenne_esperance(n): L18 loi_X=[[1,1/6],[2,1/6],[3,1/6],[4,1/6],[5,1/6],[6,1/6]] L19 echantillon=tirages(n) L20 moyenne =moyenne_val(echantillon) L21 esperance= esperance_X(loi_X) L22 dist=abs(moyenne–esperance) L23 print('taille échantillon :', n) L24 print('echantillon :', echantillon) L25 print('moyenne :', moyenne) L26 print('esperance X :', esperance) L27 print('distance moyenne-esperance :', dist) L28 return dist |
L17 : On définit la fonction ecart_moyenne_esperance qui
calcule la distance entre la moyenne d’un
échantillon de taille n et
l’espérance. L18 : On précise la loi de probabilité associée à l’expérience. L19 : On crée un échantillon de taille n. L20 : On calcule sa moyenne. L21 : On calcule l’espérance de la variable aléatoire. L22 : On calcule la distance entre les deux. L23 à L28 : On affiche quelques éléments. |
On obtient ainsi le programme complet permettant d’étudier la distance entre l’espérance d’une loi de probabilité et la valeur moyenne d’un échantillon de taille n.
Après avoir exécuté le programme, on peut effectuer quelques comparaisons :
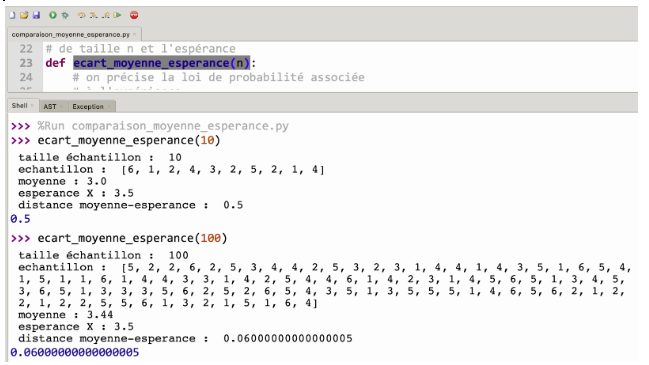
On observe que pour une petite valeur de n (n = 10), la distance entre la moyenne et l’espérance vaut 0,5, ce qui n’est pas négligeable sur un échantillon de 10 valeurs.
Pour une valeur plus importante de n (n = 100), cette distance n’est plus que d’environ 0,06, ce qui est assez peu sur un échantillon de 100.
De la même manière, on peut calculer des distances pour des valeurs de n plus importantes :
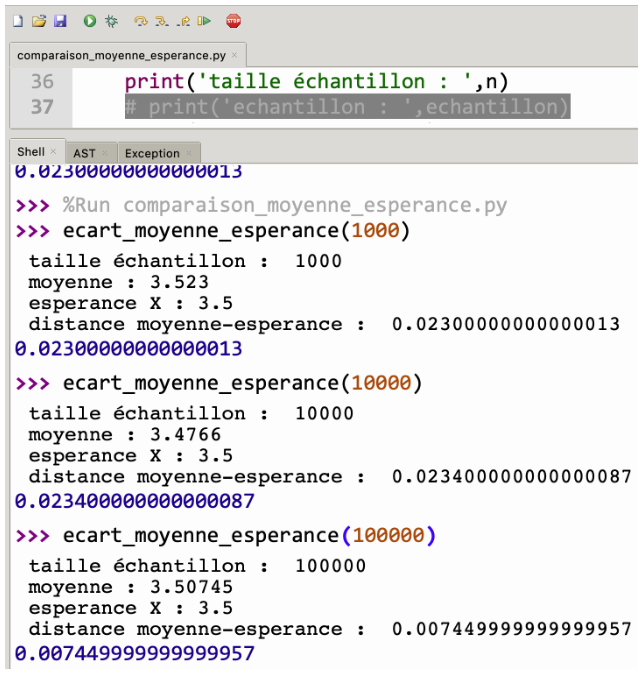
La ligne 37 du programme a été mise en commentaire pour ne plus afficher l’échantillon et ne pas surcharger l’affichage :
# print(‘echantillon :’ echantillon)
On vérifie empiriquement que plus la valeur
de n
est grande, plus la distance entre la moyenne de
l’échantillon et l’espérance
se rapproche de 0.
Autrement dit, lorsque la taille n de
l’échantillon est importante, la valeur de
la moyenne de l’échantillon se rapproche
de la valeur de l’espérance.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








