Le calcul intégral : aire sous une courbe positive et continue
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Définir l’intégrale d’une fonction continue et positive comme la mesure de l’aire d’un domaine du plan.
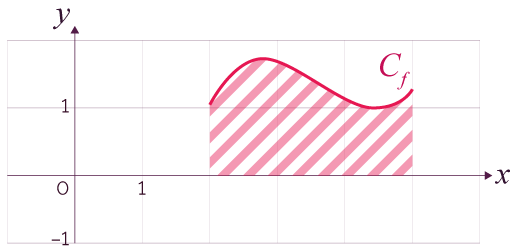
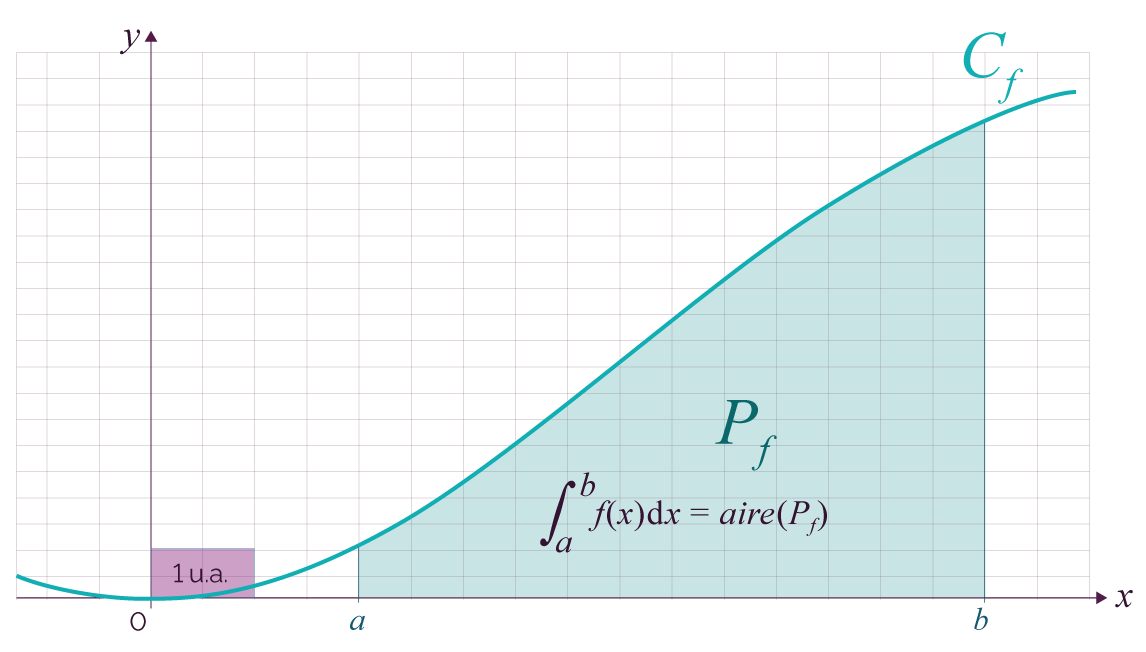
- Le domaine du plan Pf situé sous
la courbe Cf est la partie
plane délimitée par Cf , l'axe des
abscisses et les droites d'équations
x = a
et x = b :
.
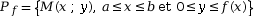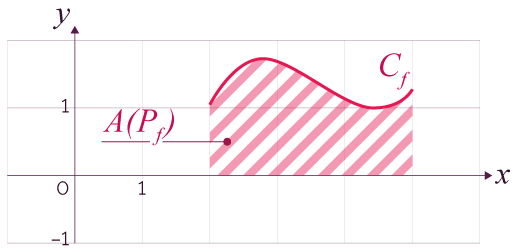
- On admet que Pf a une aire,
appelée intégrale de f sur [a ; b] :
.
-
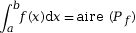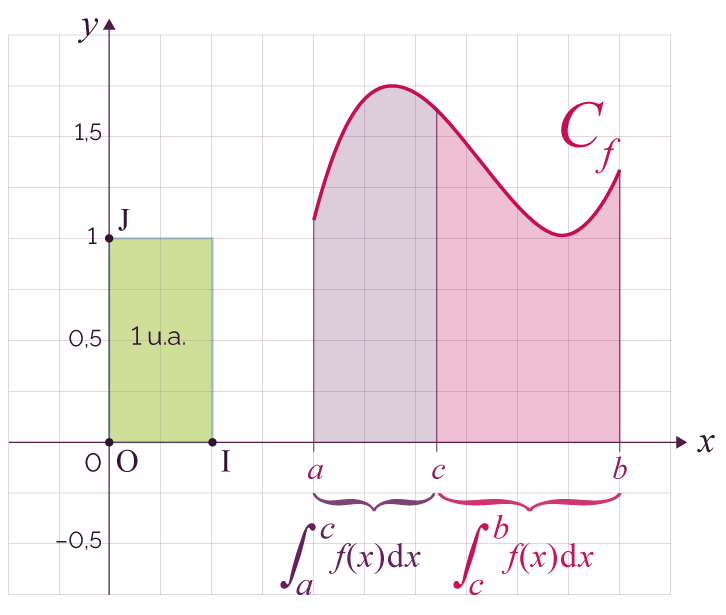
- Relation de Chasles : pour tout
nombre c de
[a ; b] :
.
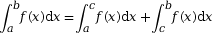- Connaitre la notion d’aire d’une figure.
- Connaitre la notion de fonction continue.
La notion d'aire (ou plus exactement de la mesure de l'aire) d'une partie plane peut sembler un concept évident. Or, la définition de cette notion est en fait difficile et ne peut être rigoureusement établie en classe de lycée.
Historiquement, on a assez vite
dégagé quelques règles que devait
suivre la notion d'aire et on a su établir les
formules donnant les aires d'un rectangle, d'un
triangle rectangle puis d'un triangle quelconque
.
Ainsi, on pouvait calculer l'aire d'une ligne
polygonale fermée quelconque comme somme des
aires de triangles et on a démontré que
cette aire était indépendante du
découpage choisi.
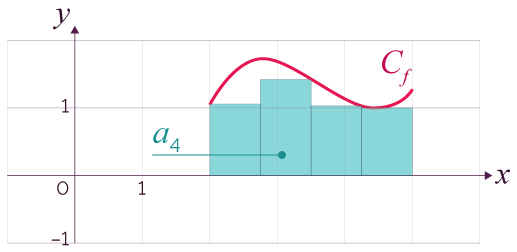
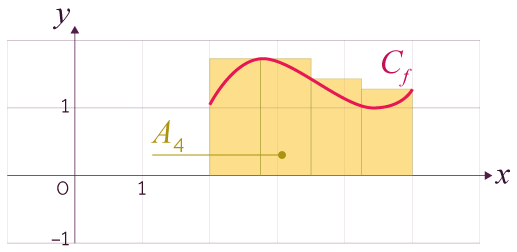
On a eu alors l’idée d’encadrer A(Pf ) par des aires (réelles) de parties du plan limitées par des lignes polygonales fermées. Voici brièvement la démarche.
Soit n un
entier naturel.
On utilise, par exemple, deux lignes polygonales
fermées sn et Sn ,
constituées chacune de n rectangles, la
première incluse dans la partie Pf , la seconde
contenant Pf .
On appelle an l'aire de sn et An l'aire de Sn.
|
|
|
|
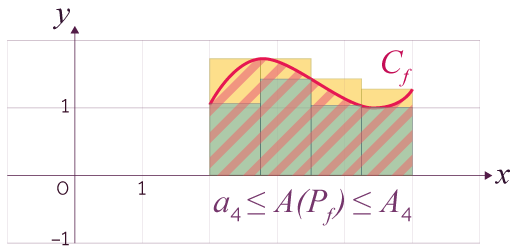
Bien sûr, on peut augmenter le nombre de rectangles pour obtenir un encadrement plus fin de A(Pf ) et même pour obtenir un encadrement aussi fin qu'on le souhaite ; autrement dit, la différence (An – an) peut être rendue aussi petite que l'on veut pourvu que n soit suffisamment grand.
Ainsi, la notion d'aire va se définir à l'aide de la notion de limite.
On démontre (et on admet ici) que les suites
(an) et
(An) sont
respectivement croissante et décroissante et que
:
; autrement dit les
suites (An) et
(an) ont une
limite finie commune, à savoir la valeur
de A(Pf).
On prouve aussi que cette limite est
indépendante du choix des
parties sn
et Sn.
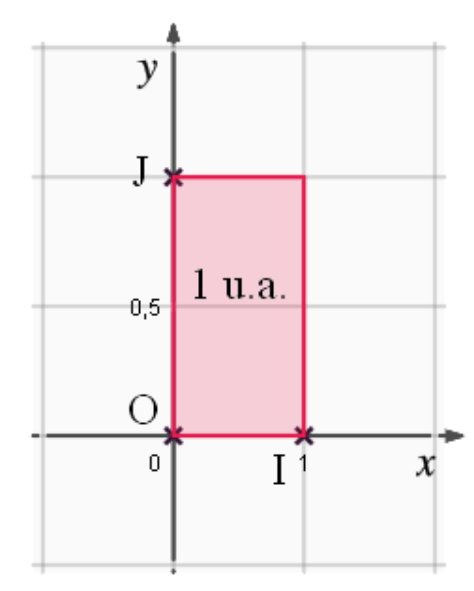
Sauf mention contraire, les aires seront
exprimées en unités d'aire.
Soit (a,
b) un couple
de réels vérifiant a ≤ b.
Soit f une
fonction continue et positive
sur [a ; b]
de courbe représentative Cf.
Si a = b, Cf se réduit à un point de coordonnées (a ; f(a)).
Autrement dit, on a Pf = {M(x ; y), a
x
b et 0
y
f(x)}.
Le domaine Pf est représenté ci-dessous en bleu.
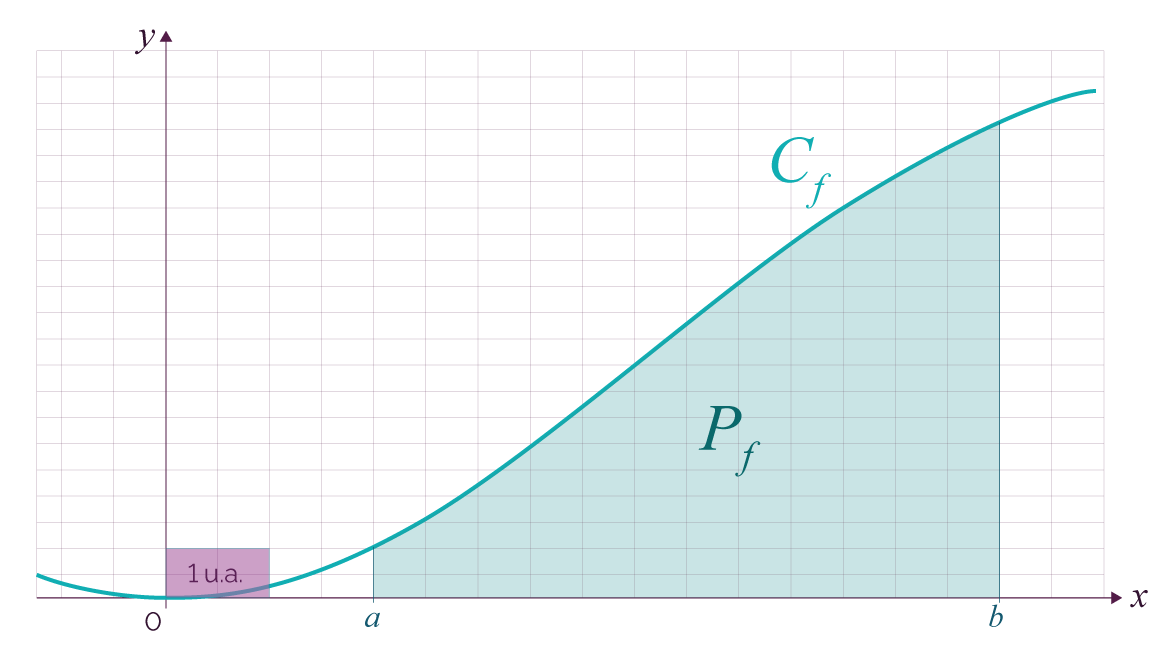
On admet que Pf a une aire.
On encadre cette aire par la somme des aires des
rectangles situés sous la courbe et la somme des
aires des rectangles situés au-dessus la
courbe.
On crée n subdivisions de
l’intervalle [a ; b].
Chaque rectangle inférieur a donc une aire
égale à 
.
Chaque rectangle supérieur a donc une aire
égale à 
.
On peut alors encadrer l’aire du domaine
Pf :
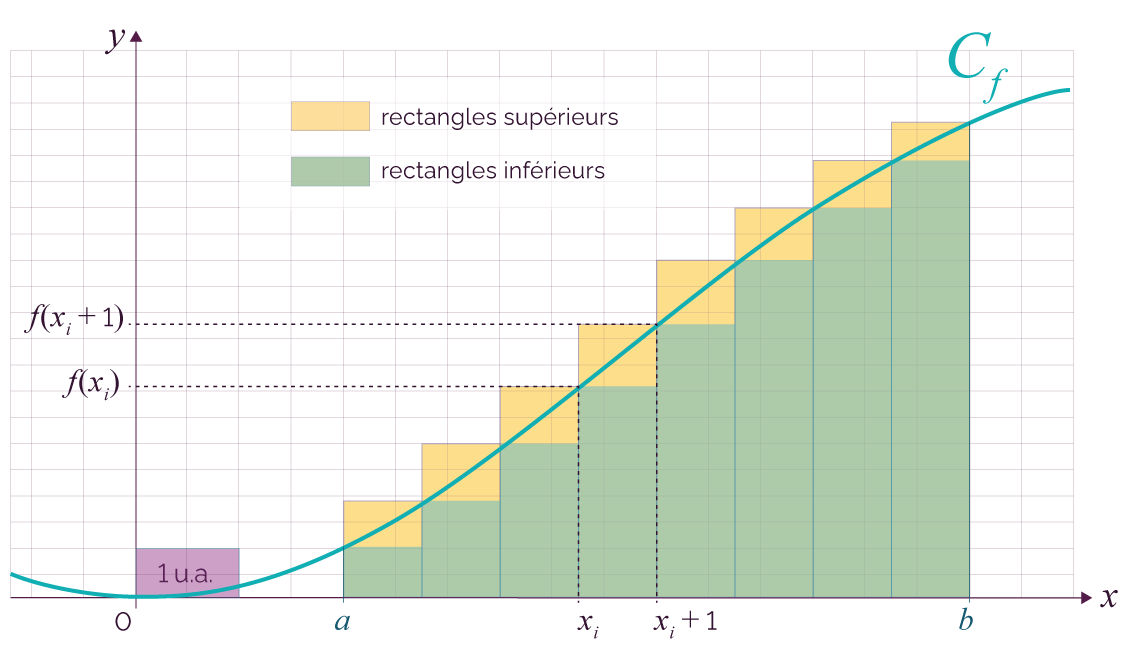
On admet que Pf a une aire appelée intégrale de f sur [a ; b].
On la note
ou 
.On a donc
= aire(Pf).
L’encadrement précédent devient :
Si l’on augmente le nombre n de subdivisions, les sommes des aires des rectangles tendent vers une limite commune égale à l’intégrale de la fonction f sur l’intervalle [a ; b].
- Le symbole
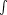ressemble à un
S allongé. Il symbolise l’idée
d’une somme.
-
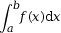se lit
« intégrale (ou somme)
de a
à b de f(x)dx ».
Dans cette écriture, x est une variable (elle varie sur l'intervalle [a ; b]), dite « muette », c’est-à-dire que l’on peut la remplacer par une autre lettre, par exemple t, sans changer la définition.
Ainsi par exemple :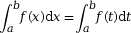
.
-
-
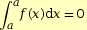
Relation de Chasles : Pour tout
nombre c de [a ; b] :
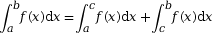
Les propriétés de l'intégrale sont abordées dans la fiche « Nouvelle définition et propriétés de l'intégrale ».
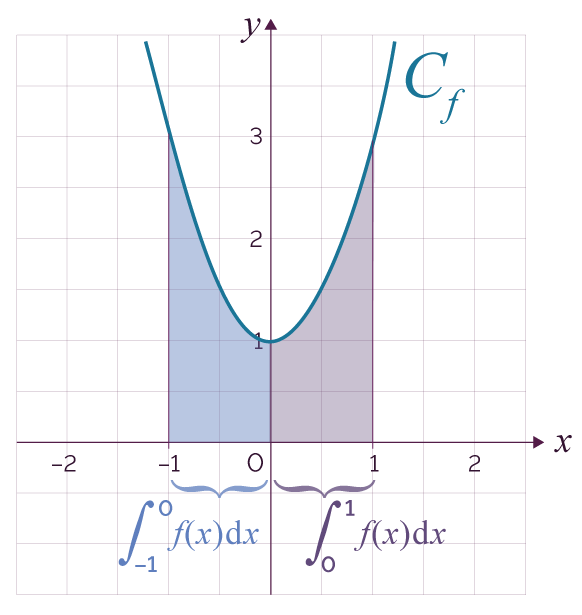
On peut utiliser l'invariance par symétrie ou translation de la notion d'aire pour calculer certaines intégrales. Par exemple, f étant une fonction paire, Cf est symétrique par rapport à l’axe des ordonnées.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Fermer
Accédez gratuitement à
