Loi binomiale, espérance et écart type- Terminale- Mathématiques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Reconnaitre un schéma de Bernoulli.
- Calculer des probabilités dans le cadre de la loi binomiale.
- Utiliser l’espérance d’une loi binomiale.
- Considérons une variable
aléatoire X qui compte le nombre de
réalisations du succès au cours des
n
épreuves. On dit que X suit une loi binomiale de
paramètre n et p.
X peut donc prendre toutes les valeurs entières de 0 à n. - On admet les résultats suivants sur
l'espérance et l'écart type d'une loi
binomiale de paramètres n et p : E(X) = np ;
V(X) = npq ;
.
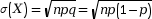- Pour un schéma de Bernoulli
d’ordre n, de
probabilité p pour chaque succès
de l’épreuve, la loi de probabilité de
la variable X qui à chaque issue
associe k succès est
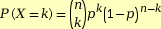avec 
.
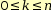Cette loi est notée ℬ(n, p).
Considérons un schéma de Bernoulli de
paramètres n et p.
Les n
épreuves de Bernoulli peuvent se
modéliser par un arbre qui aurait
2 branches initiales (succès-échec)
puis chacune de ces branches donnant naissance à
2 nouvelles branches (succès-échec),
etc.
À chaque épreuve, le nombre de branches
est doublé.
X peut donc prendre toutes les valeurs entières de 0 à n.
Prenons k
une de ces valeurs entières.
Sur l'arbre, il existe un certain nombre de branches
(ou chemins) qui comportent k succès et
n – k échecs.
Ce nombre de chemins se note 
, il s'agit du
nombre de k-uplets d'un ensemble
à n
éléments.
Il peut se calculer aisément avec une
calculatrice.
Chacun de ces chemins comporte k succès et n – k échecs. La probabilité qu'un de ces chemins se réalise est égale à pk × qn–k (c'est le principe du produit des probabilités sur les branches).
Pour finir, puisqu'il y a 
chemins ayant
chacun la probabilité pk × qn–k
de se produire, on peut en déduire que
P(X = k) = pk × qn–k.
E(X) = np ;
V(X) = npq ;
Prenons l'exemple suivant : 
.
Écrire n (ici 3) puis entrer la fonction « Combinaison » (qui est dans le menu « Math/Prb ») puis l’argument k (ici 2). Si les instructions sont en anglais, la fonction sera « nCr » dans le même menu qu’indiqué.
Dans une page calcul, entrer « nCr(3,2) ».
Écrire n (ici 3) puis entrer la fonction « nCr » (dans « OPTN » puis « PROB ») puis l’argument k (ici 2).
Pour déterminer des coefficients binomiaux, dans une cellule écrire « =COMBIN(3;2) ».
avec .Cette loi est notée ℬ(n, p).
C’est ce que l’on constate avec
l’exemple précédent. Pour
2 succès, on peut compter
« à la main » la
probabilité de chaque chemin et additionner le
tout, ce qui donne 
.
D’après la définition, pour
on a : 
.
Prenons l'exemple suivant : P(X = k) pour n = 1000, p = 0,5 et k = 462.
Entrer la fonction « binomFdp(n,p,k) » (qui est dans le menu « distrib ») avec les arguments n = 1000, p = 0,5 et k = 462.
Dans une page calcul, entrer « binomPdf(1000,0.5,462) ».
Les points sont des virgules, les virgules des caractères de séparation des variables.
Entrer la fonction « BinomialPD(k,n,p) » (dans « OPTN » puis « STAT » puis « DIST » puis « BINM » et « Bpd » pour finir) avec les arguments k = 462, n = 1000 et p = 0,5.
Pour déterminer P(X = k), dans une cellule écrire « =LOI.BINOMIALE(valeur de k ; n ; p ; FAUX) ».
Sur certains tableurs au lieu de « FAUX » il faut écrire « 0 ».
Prenons l'exemple suivant : P(X
k) pour
n = 1000,
p = 0,5 et
k = 462
(utilisé ci-après).
Entrer la fonction « binomFrép(n,p,k) » (qui est dans le menu « distrib ») avec les arguments n = 1000, p = 0,5 et k = 462.
Dans une page calcul entrer « binomCdf(1000,0.5,0,462) ».
Entrer la fonction « BinomialCD(k,n,p) » (dans « OPTN » puis « STAT » puis « DIST » puis « BINM » et « Bcd » pour finir) avec les arguments k = 462 la valeur à tester, n = 1000 et p = 0,5.
Dans une cellule écrire « =LOI.BINOMIALE(valeur de k ; n ; p ; VRAI) » que l’on tirera vers le bas.
Sur certains tableurs au lieu de « VRAI » il faut écrire « 1 ».
On peut remarquer : 
. 
, 
.
Par convention 
.
• Si 
alors 
.
• Si 
alors 
(formule de Pascal).
Ces deux règles permettent de calculer les coefficients binomiaux de proche en proche, en construisant le « Triangle de Pascal » par exemple, ce qui se fait assez facilement sur tableur.
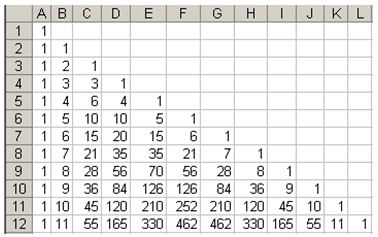
Dans le tableur, on enlève l’affichage des
zéros (cliquer sur Outils/Options puis
décocher la case « Valeurs
zéro » dans Affichage).
On place des 1 en première colonne et en
diagonale.
En B3, on écrira une formule comme
« =A2+B2 » que l’on recopie
vers le bas. On recopie aussi cette formule vers la
droite pour les cellules sans valeur à
l’intérieur du triangle.
Les coefficients binomiaux sont obtenus avec la calculatrice.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Fermer
Accédez gratuitement à
