Fiche de cours

La mesure des inégalités

Lycée > Terminale > SES > La mesure des inégalités

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectifs

Savoir mesurer les inégalités.
Savoir interpréter les principaux outils de mesure des inégalités.

Points clés

La disparité est la mesure de l’écart entre les valeurs centrales qui caractérisent une ou plusieurs populations statistiques.
La dispersion mesure l’écart entre les valeurs extrêmes d’une même population statistique.
La moyenne arithmétique (ou moyenne simple) est la moyenne calculée de telle sorte que chaque variable de la population étudiée a le même poids dans le calcul.
La moyenne pondérée tient compte du poids qu’a chaque valeur.
On peut interpréter la mesure des inégalités à partir de la courbe de Lorenz. Plus la courbe de Lorenz s’éloigne de la bissectrice, plus le pays présente des inégalités de revenu et de patrimoine.
Le coefficient de Gini exprime les inégalités en calculant l’aire entre la courbe de Lorenz et la bissectrice. Plus le coefficient est proche de 1, plus le pays est égalitaire, plus il est proche de zéro et plus il est inégalitaire.

Pour bien comprendre

Les inégalités économiques sont les différences entre individus ou groupes sociaux portant sur des avantages ou des désavantages économiques et qui fondent une hiérarchie entre ces individus ou entre ces groupes.
Les inégalités sociales sont les différences entre individus ou groupes sociaux portant sur des avantages ou des désavantages dans l’accès à des ressources socialement valorisées.

1. La mesure des inégalités

a. Disparité et dispersion

La disparité est la mesure de l’écart entre les valeurs centrales qui caractérisent une ou plusieurs populations statistiques.

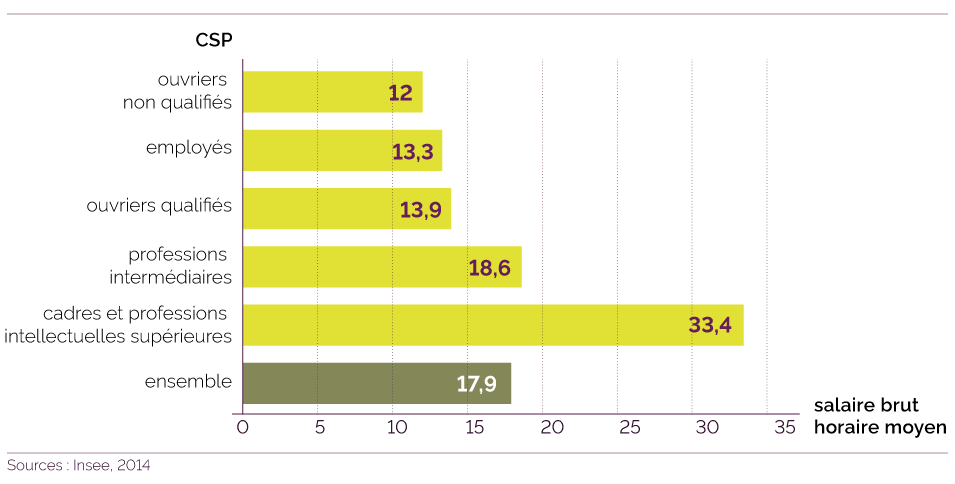Le salaire brut horaire en fonction de la CSP

Méthode : Ici, les cadres gagnent 15,5 € de l’heure de plus que l’ensemble de la population, tandis que les ouvriers non qualifiés gagnent 5,9 € de l’heure de moins que l’ensemble de la population. Ainsi, la disparité mesure l’écart entre l’ensemble et la catégorie qui gagnent les plus et entre l’ensemble et la catégorie qui gagnent le moins.

La dispersion mesure l’écart entre les valeurs extrêmes d’une même population statistique.

Méthode : Ici la dispersion est donc la différence entre le salaire des cadres (33,4 €) et celui des ouvriers non qualifiés (12 €), soit 21,4 €.

b. Moyenne et médiane

Pour mesurer la disparité il faut utiliser des indicateurs de valeur centrale d’une population statistique : moyenne et médiane.

1. Les moyennes

On peut calculer deux types de moyennes.

La moyenne arithmétique (ou moyenne simple) est la moyenne calculée de telle sorte que chaque variable de la population étudiée a le même poids dans le calcul.

Méthode de calcul : (Valeur 1 + Valeur 2 + Valeur 3 + …) ÷ Effectif

Exemple : Si je cours une première fois 5 kms en 45 mn, la deuxième fois en 40 mn, la troisième fois en 35 mn et la 4ème en 30mns, je cours en moyenne donc
(45 + 40 + 35 + 30) ÷ 4 = 37,5 mn pour parcourir 5 kms.

La moyenne pondérée tient compte du poids qu’à chaque valeur. On va pondérer chaque valeur d’un coefficient.

Méthode de calcul : (Valeur 1 x coefficient) + (Valeur 2 x coefficient) + ... ÷ Effectif

Exemple : Si j’ai 12 en maths coefficient 16, 16 en SES coefficient 16 et 14 en philo coefficient 5, ma moyenne à l’épreuve nationale écrite sera de
((12 x 16) + (16 x 16) + (14 x 5) ÷ (16 + 16 + 5) =
192 + 256 + 70 ÷ 37 =
14 ÷ 60.

2. La médiane

La médiane est la valeur d’une série statistique qui divise en 2 groupes égaux la population étudiée.

Exemple : Si il y a 10 élève la médiane se situe au 5^e élève.

Méthode : Lorsqu’on ordonne les observations d’une variable, la valeur médiane correspond à l’observation qui se trouve au point milieu de cette liste ordonnée (la valeur du milieu d’un ensemble de données ordonnées). Elle correspond plus précisément à un pourcentage cumulé de 50 % (c’est-à-dire que 50 % des valeurs sont supérieures à la médiane et 50 % lui sont inférieures).
La position de la médiane est : la valeur à la position (n + 1) ÷ 2, le n désignant le nombre de valeurs dans un ensemble de données.
Pour calculer la médiane, il faut d’abord ordonner les données (les trier dans l’ordre ascendant). La médiane est le nombre qui se situe au point milieu.

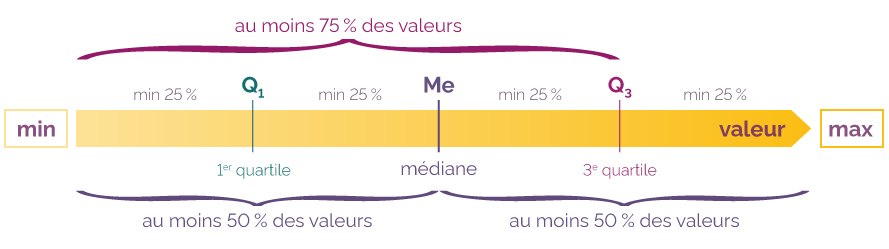La médiane

c. Les quantiles

1. Les déciles

Un décile est la valeur d’une variable étudiée qui partage l’effectif total d’une série en 10 groupes égaux, c’est-à-dire contenant chacun 10 % de l’effectif total.

Il y a neuf déciles (notés D1, D2, … D9). D1 est tel que 10 % de l’effectif total lui sont inférieurs et donc 90 % supérieur.

Méthode : 10 % des moins riche ont un revenu qui s’élève au maximum à 12 930 € et les 10 % les plus riches ont un revenu qui s’élève au minimum à 59 900 €.

Distribution des revenus disponibles des ménages (en euros)

	2009
1er décile (D1)	12 930
2e décile (D2)	16 660
3e décile (D3)	20 190
4e décile (D4)	24 290
Médiane (D5)	28 740
6e décile (D6)	33 640
7e décile (D7)	39 260
8e décile (D8)	46 880
9e décile (D9)	59 900
Rapport interdécile (D9/D1)	4,9

Méthode de lecture : en 2009, 10 % des ménages ont un revenu disponible inférieur à 12 930 euros.

2. Les autres quantiles

Tout dépend de nombre de groupes :

les quartiles : 4 groupes (25 % des effectifs chacun) ;
les quintiles : 5 groupes (20 % des effectifs chacun) ;
les vingtiles : 20 groupes (5 % des effectifs chacun) ;
les centiles : 100 groupes (1 % des effectifs chacun)

3. Les écarts interquantiles

Pour résumer la dispersion d’une série, on peut calculer :

l’intervalle interdécile (D9 – D1) ;

On exclut les 2 intervalles extrêmes qui sont susceptibles de comporter des valeurs marginales (les plus « riches » ou les plus « pauvres »).

Exemple : En 2009, l’intervalle interdécile est de (D9-D1) 59 900-12 930 = 46 970 €.

le rapport interdécile (D9 / D1).

Le calcul de ce rapport est encore plus intéressant, car il se « débarrasse » de l’unité dans laquelle les valeurs sont exprimée (ici en €)

Exemple : En 2009, le rapport interdécile est de (D9/D1) 59 900 / 12 930 = 4,6 ce qui signifie que les 10 % les plus riches ont un revenu 4,6 fois supérieur à celui des 10 % les moins riches.

Ainsi, il existe différents outils pour mesurer les inégalités.

2. L’interprétation de la mesure des inégalités

a. La courbe de Lorenz

Il s’agit d’une représentation graphique permettant de « visualiser » la concentration des valeurs observées. La lecture de la courbe de Lorenz se fait ainsi :

sur l’axe des abscisses on trouve les pourcentages cumulés croissants des effectifs (10 % de la pop, 20 % de la pop, …, 100 % de la pop), c’est-à-dire les déciles, quartiles, etc. ;
sur l’axe des ordonnées on trouve les pourcentages cumulés croissants de la variable étudiée (10 % des revenus, 20 % des revenus, …, 100 % des revenus).

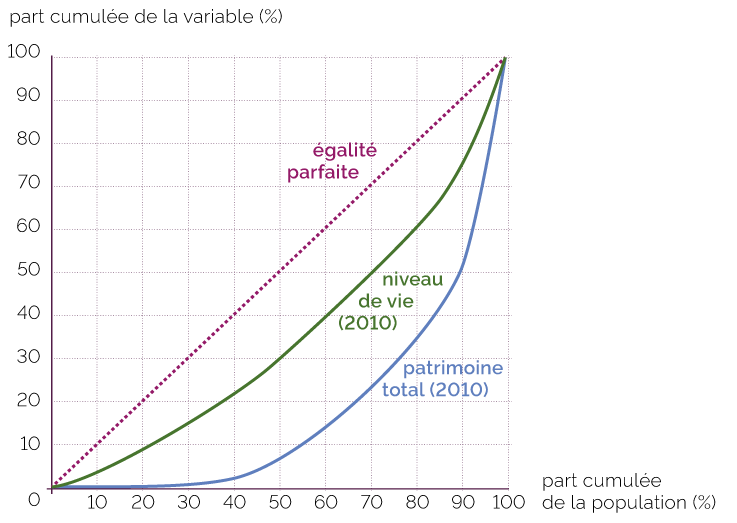La courbe de Lorenz

Méthode de lecture
En 2010, les 10 % des ménages les moins aisés percevaient environ 3 % du RDB national et 0 % du Patrimoine,
En 2019, les 10 % les plus aisés percevaient (100-75 %) 25 % des RDN national et 50 % du patrimoine.

Interprétation de la forme de la courbe de Lorenz :

la bissectrice (diagonale) représente une répartition égalitaire des revenus : les 10 % les plus pauvres perçoivent 10 % des revenus, les 20 % les + pauvres perçoivent 20 % des revenus …
plus la courbe est creuse, c’est-à-dire éloignée de la diagonale, plus la concentration est forte; plus la courbe est proche de cette diagonale, plus la répartition est égalitaire.

b. Le coefficient de Gini

Le coefficient de concentration de Gini est obtenu à partir de la courbe de Lorenz. On mesure la concentration d'une distribution en la comparant à une distribution qui serait la plus inégale possible.

Le coefficient de Gini varie entre 0 et 1 : plus on est proche de zéro, plus il y a d'égalité, à l'inverse, plus le coefficient de Gini se rapproche de 1, plus le caractère étudié est inégalitaire.

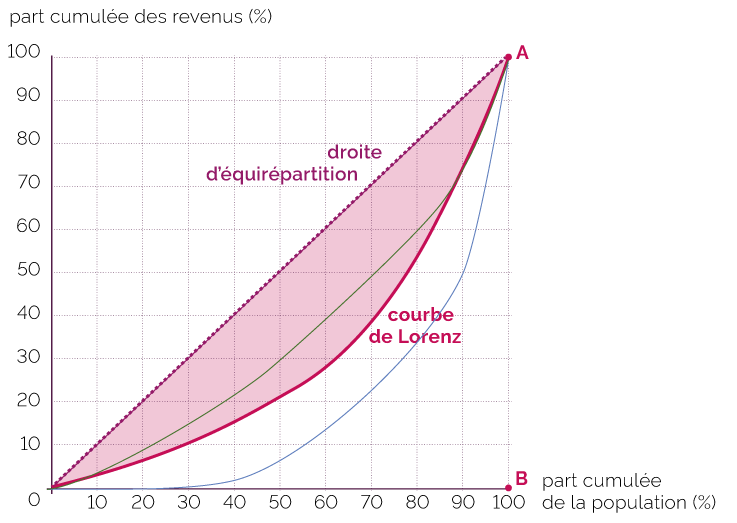Le coefficient de Gini

Méthode : Pour calculer le coefficient de Gini, il faut diviser l’aire entre la bissectrice et la courbe de Lorenz par l’aire du triangle OAB qui divise l’aire de la surface en deux.

En France, le coefficient de Gini est de 0,3 pour les revenus et de 0,6 pour les patrimoines. La distribution des patrimoines est donc plus inégalitaire que celle des revenus.

Ainsi, la courbe de Lorenz et le coefficient de Gini sont les meilleurs outils pour interpréter les inégalités.

En conclusion, il existe de nombreux outils pour mesurer et interpréter les inégalités.

Évalue ce cours !

Note 4.1 / 5. Nombre de vote(s) : 8

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT