Utiliser la formule de l'énergie potentielle de pesanteur
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Connaitre la définition d’une force conservative.
- Connaitre et savoir utiliser l’expression de l’énergie potentielle de pesanteur.
- L’énergie potentielle de pesanteur est notée Epp et s’exprime par Epp = m × g × z.
- Une force est conservative lorsque le travail d’une force entre deux points donnés est indépendant du chemin suivi.
- La variation d’énergie potentielle
associée au poids
,
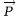entre deux points A et B, est égale à
l’opposé du travail de ce poids sur le
système : 
.
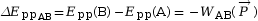- Force
- Travail d’une force
- Énergie
Un système de masse m évolue dans le
champ de pesanteur 
. Le système est déplacé
d’un point A à un
point B,
d’altitudes respectives zA et zB.
Dans un premier temps, le déplacement entre les deux points est rectiligne.
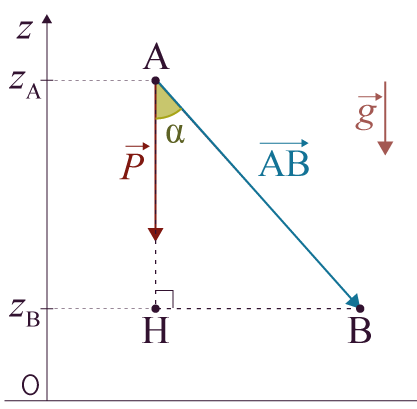
Schéma de la situation
On applique alors la formule du travail pour estimer le
travail du poids :
.
Le travail du poids
s’exprime par 
.Dans le triangle rectangle AHB,
avec AH = zA − zB.Ainsi, AB × cos(α) = AH = zA − zB.
On a donc
.
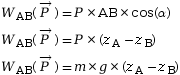On considère maintenant que le déplacement n’est plus rectiligne mais segmenté en deux parties entre les points de départ A et d’arrivée C.
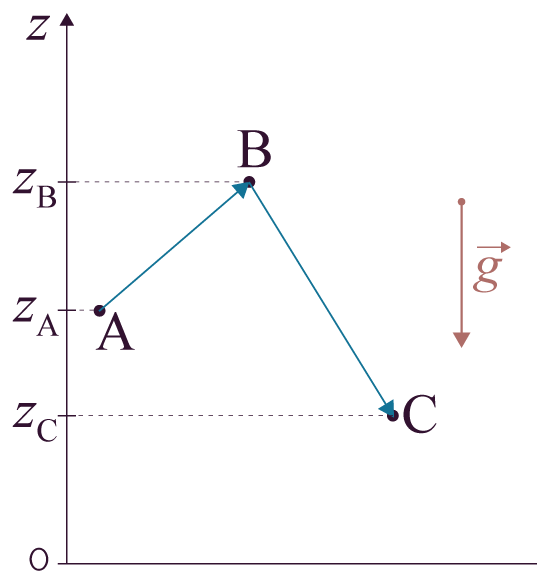
Schéma de la situation
Dans la configuration décrite par le schéma ci-dessus, la trajectoire est composée de deux segments de droites.
Le travail est une grandeur additive,
on décompose donc le travail du poids
entre A
et C de la
manière suivante :
Le résultat précédent est généralisable : toute trajectoire du système peut être vue comme une infinité de déplacements possibles, ce qui mène au même résultat.
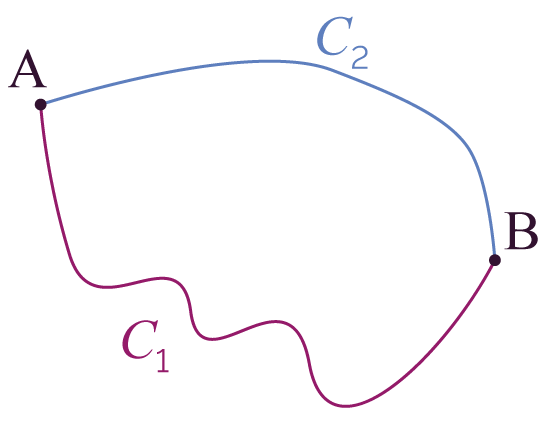
Chemins C1 et C2 pris pour aller
d’un point A à un point B
En conclusion, pour utiliser la relation 
, il est inutile de connaitre le chemin suivi
du système pour aller de A à B.
Le poids est une force conservative.
Lorsque le travail d’une force entre deux points donnés dépend du chemin suivi, on dit que la force est non conservative.
L’énergie potentielle associée au
poids 
est appelée « énergie
potentielle de pesanteur ».
La valeur de l’énergie potentielle de pesanteur est égale au produit de la masse m du système, de l’intensité de la pesanteur g et de l’altitude z du centre de gravité G de ce système.
|
Epp = m × g × z |
avec :
|
- L’altitude z est donnée par rapport à une origine qu’il faut préciser. On choisit la plus commode. On a ainsi Epp = 0 pour z = 0 (point de référence choisi).
- Un système possède une énergie potentielle uniquement s’il est soumis à des forces conservatives car l’énergie potentielle ne dépend que des altitudes finales et initiales, et non du chemin suivi.
On lâche une balle d’un
point A
à un point B. Cette balle n’est
soumise qu’à son poids 
, qui est une force conservative
(son travail ne dépend pas des positions de
départ et d’arrivée).
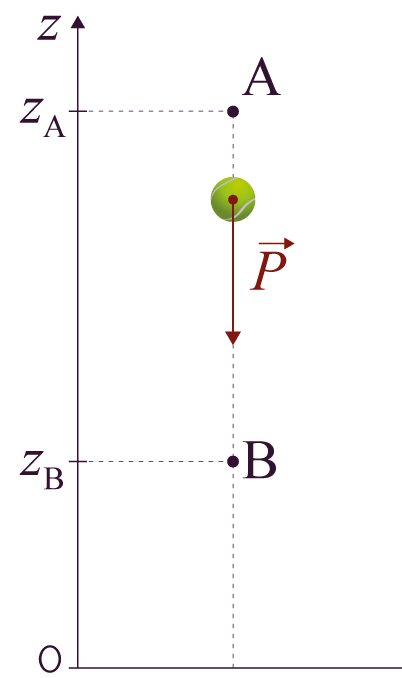
Schéma de la situation
On calcule le travail du poids entre A et B.
avec α l’angle
entre 
et 
. Or 
et 
sont colinéaires et de même sens,
donc α = 0° et
cos(α) = 1.
On a donc :
Le travail fourni par la force
conservative 
pour déplacer la balle du
point A vers
le point B
peut s’exprimer en fonction de m × g × z,
qui représente l’énergie
potentielle de pesanteur.
|
|
avec :
|
le travail du
poids 
appliqué sur le
système, en joule (J)
d’un système entre A et B est le travail à
fournir pour compenser le poids lors du changement
d’altitude par rapport à la Terre.La variation d’énergie potentielle de pesanteur associée au poids P est donc égale à l’opposé du travail de cette force sur le système.
On lance un ballon de masse m = 500 g du dernier étage de la tour Eiffel (à 307 m d’altitude).
Schéma de la situation
Si on choisit le sol comme origine des altitudes, le point B est à l’altitude zB = 307 m et le point A est à l’altitude zA = 0 m.
La variation d’énergie potentielle de
pesanteur Epp de ce ballon
est :
L’énergie potentielle de pesanteur Epp correspond au cas où le système est soumis à la force conservative du poids
.Si le système est soumis à une autre force conservative
(force électrique par exemple)
entre A
et B,
on applique la formule dans le cas
général : 
.Dans ce cas, on parle de variation d’énergie potentielle ΔEp.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Physique Chimie
Exploiter la conservation de l'énergie mécanique
Physique Chimie
Calculer le travail d'une force non conservative
Physique Chimie
Étudier l'évolution des énergies d'un système
Physique Chimie
Décrire la propagation d'une onde mécanique progressive
Physique Chimie
Visualiser expérimentalement la propagation d'une onde mécanique
Physique Chimie
Réaliser une chronophotographie pour étudier la propagation d'une onde mécanique
Physique Chimie
Déterminer expérimentalement la célérité d'une onde
Physique Chimie
Les relations d'une onde mécanique périodique
Physique Chimie
Utiliser les relations de conjugaison et de grandissement pour des calculs
Physique Chimie
Déterminer les caractéristiques de l'image d'un objet
Fermer
Accédez gratuitement à
