Étudier l'évolution des énergies d'un système
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Utiliser un logiciel de traitement d’images pour étudier l’évolution des énergies cinétique, potentielle et mécanique d’un système dans le cas de la chute d’un corps.
- Le mouvement de chute libre de la balle se traduit par une conversion d’énergie potentielle de pesanteur en énergie cinétique.
- L’énergie mécanique est conservée.
- Énergies cinétique, potentielle et mécanique
- Travail d’une force
- Vitesse, chronophotographie
On souhaite étudier l’évolution des énergies d‘un système. On va pour cela étudier la chute libre d’une balle.
On étudie la chute libre d’une balle de masse m = 40,0 g, lâchée sans vitesse initiale, et évoluant dans le champ de pesanteur considéré comme uniforme. L’intensité de pesanteur est g = 9,81 N·kg−1.
On dispose pour cela verticalement une règle qui va nous servir de repère. On lâche la balle à l’extrémité de l’axe de la règle et on enregistre le mouvement de la balle grâce à une webcam réglée pour prendre 50 images par seconde.

Schéma du montage
Les images capturées sont traitées par informatique. Cela génère la chronophotographie ci-dessous, où 11 points numérotés sont représentés, de M0 (position initiale) à M10.
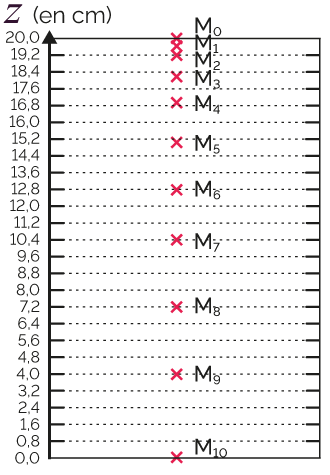
Chronophotographie de la balle
On souhaite étudier l’évolution des énergies de ce système. On va pour cela analyser cette chronophotographie selon la méthode suivante.
|
Grâce aux graduations de la règle, on établit la distance parcourue D de la balle, selon un axe vertical dirigé vers le haut dont l’origine est la position initiale M0 pour zinitial = 20,0 cm.
La webcam prend 50 images par seconde :
entre deux images successives,
il s’écoule une durée
constante |
|
|||||||||||||||||||||||||
La vitesse moyenne d’une balle se déplaçant en ligne droite entre un point A et B est donnée par la relation suivante.
|
|
avec :
|
En conséquence, la vitesse vi de la balle au point Mi est estimée par la formule approchée suivante.
|
|
avec :
|
La vitesse au point M5 est
v5 = 1,0 m·s−1.
- On prend la valeur absolue car la vitesse doit toujours être positive.
- La vitesse v0 est nulle car la balle est lancée sans vitesse initiale.
- La vitesse v10 n’est pas calculable avec cette chronophotographie.
À partir de la vitesse de la balle, on calcule son énergie cinétique en utilisant la relation suivante.
|
|
avec :
|
Pour le point M5, l’énergie cinétique de la balle est :
La balle est soumise à son poids ![]() donc elle dérive d’une
énergie potentielle de
pesanteur Epp.
donc elle dérive d’une
énergie potentielle de
pesanteur Epp.
Pour la déterminer, il faut au préalable choisir l’origine des potentiels, c’est-à-dire fixer l’altitude pour laquelle Epp sera prise comme nulle.
On choisit cette origine au bas de la règle, lorsque la balle a atteint l’altitude z = 0 m (sa position initiale étant zinitial = 0,20 m).
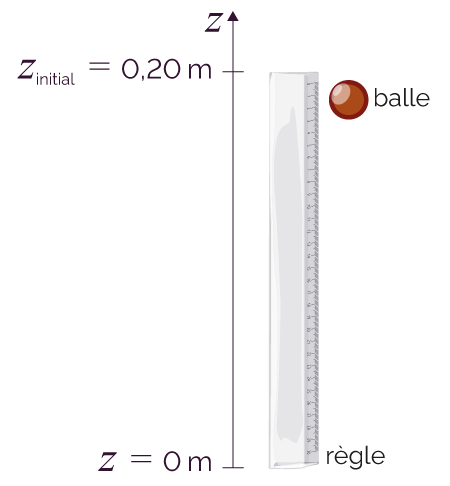
Schéma de la règle
À partir de la position z, on peut calculer l’énergie potentielle de pesanteur de la balle grâce à la relation suivante.
|
Epp = m × g × z |
avec :
|
Puisque notre repère est orienté vers le
haut, l’énergie potentielle au
point Mi est donnée
par ![]() = m × g × zi avec
zi l’altitude
du point Mi.
= m × g × zi avec
zi l’altitude
du point Mi.
L’énergie potentielle de pesanteur en M5, avec z5 =15,1 × 10−2 m, vaut :
Pour chaque point, on est maintenant en mesure de calculer l’énergie mécanique grâce à la relation suivante.
|
Em = Ec + Epp |
avec :
|
L’énergie mécanique en M5 est égale à :
Pour chaque point, on procède aux calculs précédents.
On regroupe ensuite tous les résultats dans le tableau ci-dessous.
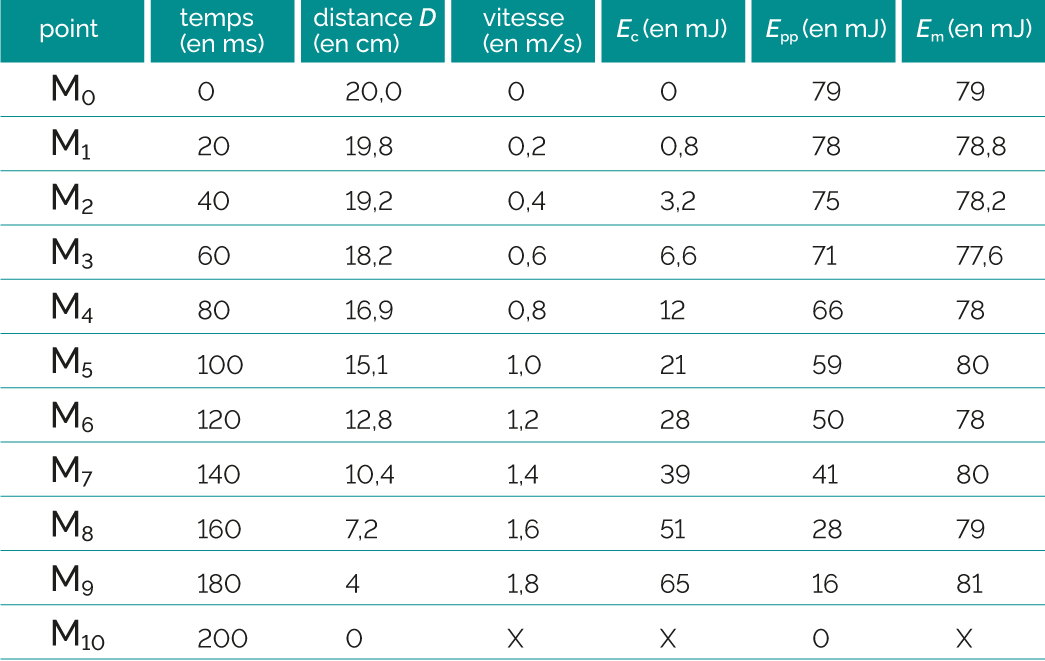
On trace l’évolution de l’énergie cinétique, de l’énergie potentielle et de l’énergie mécanique de la balle, en fonction du temps.
On obtient le graphique ci-dessous.
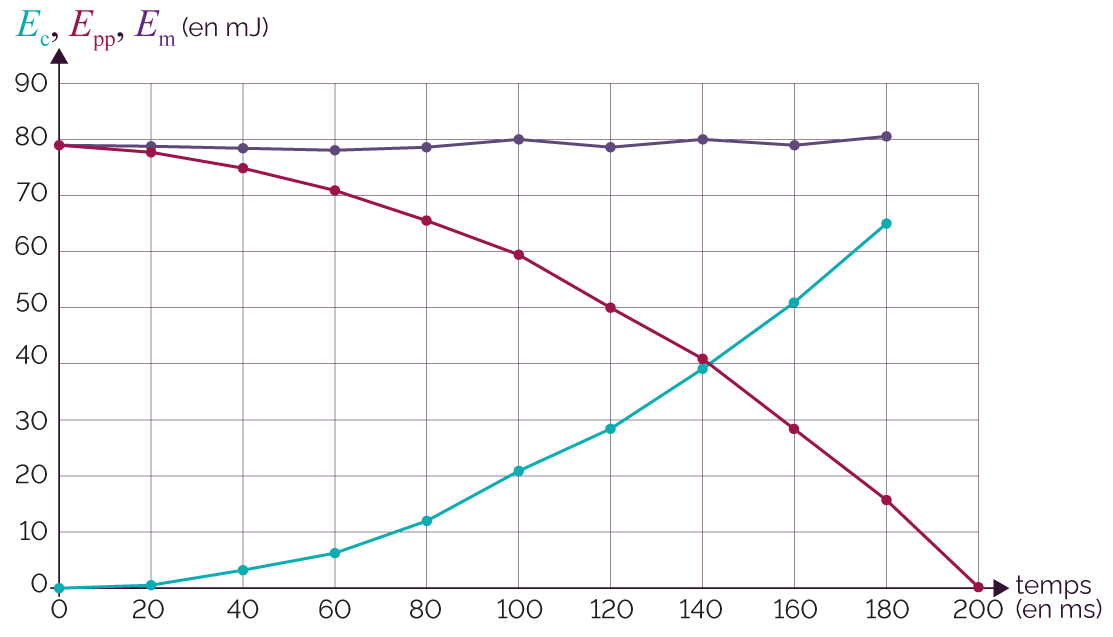
Représentation des énergies de la balle en fonction du temps
La chute de cette balle donne les résultats suivants.
- Son énergie potentielle Epp diminue car cette balle se rapproche du sol.
- Sa vitesse augmente, donc son énergie cinétique Ec augmente également.
- Lorsque l’énergie potentielle Epp diminue, l’énergie cinétique Ec augmente : l’énergie est donc transférée d’une forme à une autre.
- L’énergie mécanique Em est bien la somme des énergies cinétique Ec et potentielle Epp : Em = Ec + Epp.
- L’énergie mécanique Em est constante au cours du temps. Les quelques fluctuations observées sont explicables par les incertitudes de mesure des positions.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








