Exploiter la conservation de l'énergie mécanique
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Savoir dans quel cas l’énergie mécanique se conserve.
- Connaitre la formule de la variation de l’énergie mécanique dans le cas où le système est soumis à des forces non conservatives.
- L’énergie mécanique Em d’un système est la somme de son énergie cinétique Ec et de ses énergies potentielles Ep.
- Lors d’un déplacement entre un
point A et un
point B :
-
Em est conservé
si le système est soumis à des forces
conservatives (
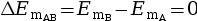 ) ;
) ;
-
Em n’est pas
conservé si le système est soumis
à des forces non conservatives (
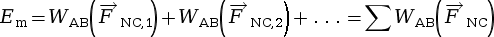 ).
).
-
Em est conservé
si le système est soumis à des forces
conservatives (
- Énergie cinétique, énergie potentielle
- Force et travail d'une force
Soit un système de masse m, dans un référentiel supposé galiléen.
| Em = Ec + Ep |
avec :
|
L’expression de l’énergie cinétique est la suivante.
|
|
avec :
|
L’expression de l’énergie potentielle Ep dépend des forces appliquées. Lorsque le système évolue en changeant d’altitude, il possède une énergie potentielle de pesanteur Epp.
| Ep = Epp = m × g × z |
avec :
|
Il y a deux forces qui dérivent d’une énergie potentielle : le poids
Une force est conservative si son travail sur un
déplacement [AB] ne dépend pas du
chemin suivi.
Lorsque la force ![]() est conservative, on a un
travail identique de cette force pour les deux chemins
possibles C1
et C2.
est conservative, on a un
travail identique de cette force pour les deux chemins
possibles C1
et C2.
|
|
avec :
|
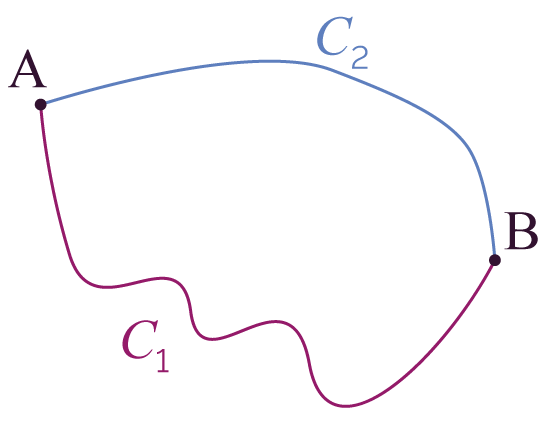
Chemins C1 et C2 pris pour aller
d’un point A à un point B
À l’inverse, une force non conservative est une force dont le travail dépend du chemin suivi.
Le poids
La force de frottement
Lors du mouvement d’un système entre un point A et un point B, la conservation de l’énergie mécanique Em de ce système va dépendre des forces appliquées au système.
![]()
Les variations de Ec et Ep se compensent ainsi au cours du temps.
![]()
Il y a donc des transferts d’énergie entre Ep et Ec au cours du déplacement du système entre les points A et B.
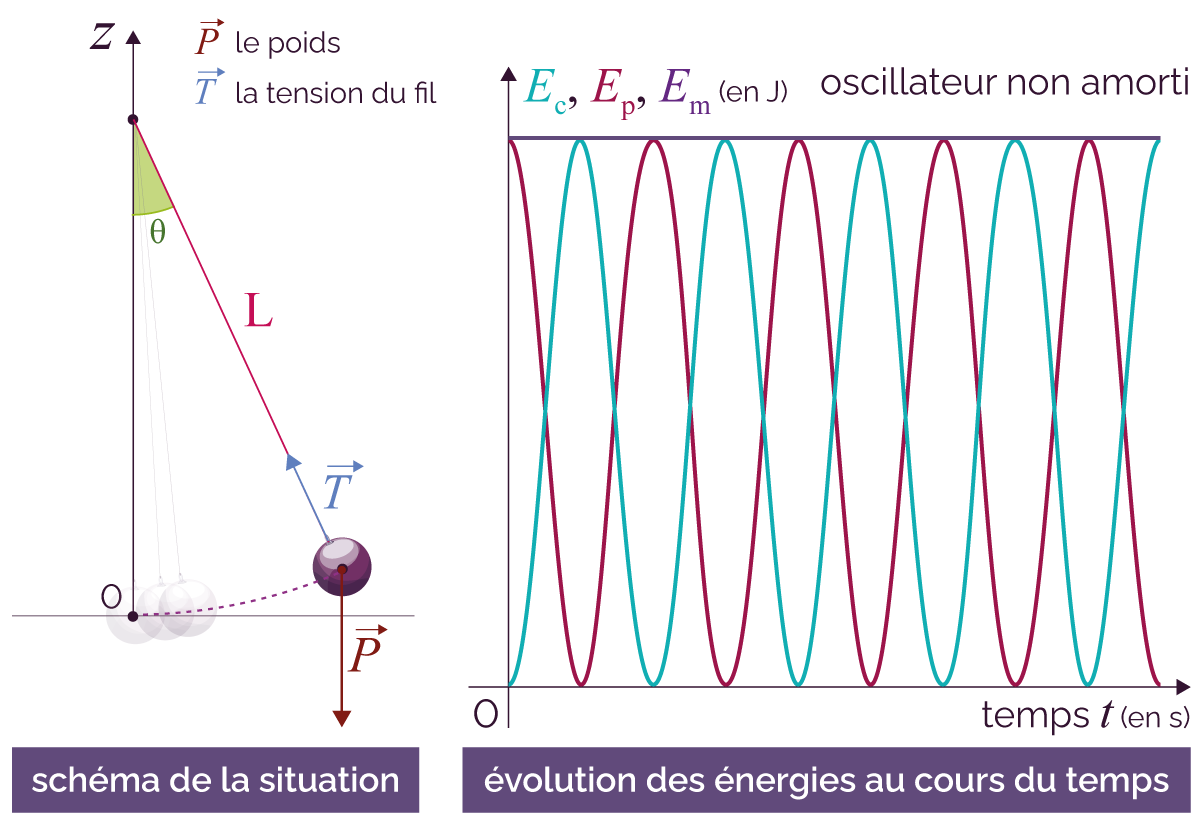
- l’énergie mécanique Em est bien la somme des énergies cinétiques Ec et potentielles Ep ;
- l’énergie mécanique est constante au cours du temps ;
- lorsque l’énergie potentielle Ep diminue, l’énergie cinétique Ec augmente : l’énergie est donc transférée d’une forme à une autre.
La variation d’énergie
mécanique ![]() du système correspond
alors à la somme du travail de chaque force non
conservative
du système correspond
alors à la somme du travail de chaque force non
conservative ![]() .
.
![]()
Si le travail de ces forces est négatif, alors
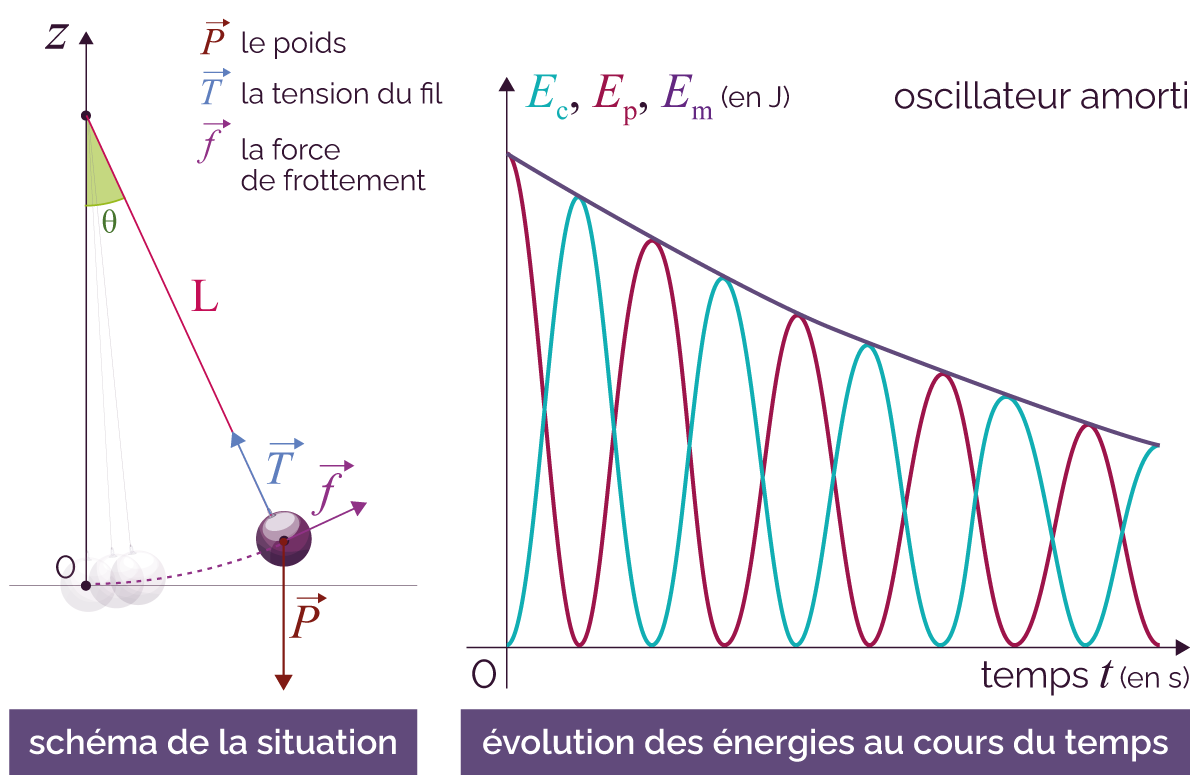
- l’énergie mécanique Em est bien la somme des énergies cinétiques Ec et potentielles Ep ;
- l’énergie mécanique décroit au cours du temps, elle n’est pas constante ;
- lorsque l’énergie potentielle Ep diminue, l’énergie cinétique Ec augmente : l’énergie est donc transférée d’une forme à une autre ;
- les courbes représentatives des énergies montrent bien que le système effectue des oscillations au cours du temps.
On étudie un système qui se déplace d’un point A à un point B.
Pour résoudre un problème en utilisant l’énergie mécanique, il faut respecter les étapes suivantes.
On présente le système, on fait le bilan des forces appliquées au système puis on les représente sur un schéma.
On calcule les énergies cinétiques et potentielles du système étudié au point A : Ec(A) et Ep(A) à l’état initial.
On en déduit l’énergie mécanique au point A : Em(A) = Ec(A) + Ep(A).
On calcule les énergies cinétiques et potentielles du système étudié au point B : Ec(B) et Ep(B) à l’état initial.
On en déduit l’énergie mécanique au point B : Em(B) = Ec(B) + Ep(B).
- Cas de la conservation de Em : on
applique la relation
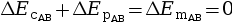 et on en déduit
l’inconnue du système.
et on en déduit
l’inconnue du système.
- Cas de la non conservation de Em : on
applique la relation
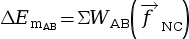 pour en déduire le
travail des forces non conservatives
pour en déduire le
travail des forces non conservatives 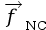 .
.
Un corps de masse m est lancé
en A avec une
vitesse ![]() . Durant son mouvement, il
n’est soumis qu’à son
poids
. Durant son mouvement, il
n’est soumis qu’à son
poids ![]() , les frottements étant
négligés : c’est le cas de la
chute libre sans frottements.
, les frottements étant
négligés : c’est le cas de la
chute libre sans frottements.
On travaille dans le référentiel
terrestre, qui est galiléen pour des temps
courts.
On cherche à déterminer la
vitesse vB du corps
quand il arrive au point B. On choisit l’altitude
de B comme
origine des altitudes. L’altitude
de A est
égale à h.
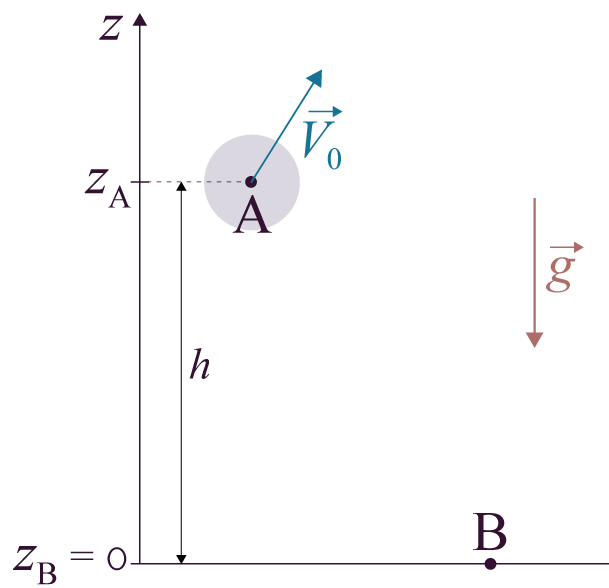
Schéma de la situation
Le système est le corps de masse m. Il n’est soumis qu’à son poids P.
On calcule l’énergie mécanique du corps en A : Em(A) = Ec(A) + Ep(A).
La seule énergie potentielle à prendre en compte est l’énergie potentielle de pesanteur Epp car ce corps est soumis à son poids.
On a donc Em(A) = Ec(A) + Epp(A) = ![]() × m × vA2 + m × g × zA,
× m × vA2 + m × g × zA,
d'où Em(A) = ![]() × m × V02 + m × g × h.
× m × V02 + m × g × h.
On calcule l’énergie mécanique du
corps en B :
Em(B) = Ec(B) + Epp(B) = ![]() × m × vB2 + m × g × zB.
× m × vB2 + m × g × zB.
Puisque zB = 0,
on a Em(B) = ![]() × m × vB2.
× m × vB2.
Il n’y a pas de forces non conservatives agissant
sur le corps, donc son énergie mécanique
est conservée.
Em(A) = Em(B),
soit ![]() × m × V02 + m × g × h =
× m × V02 + m × g × h = ![]() × m × vB2,
× m × vB2,
donc V02 + 2 × g × h = vB2,
d'où ![]() .
.
On reprend l’exemple précédent mais
cette fois-ci la masse est soumise à des forces
de frottements dues à
l’air ![]() .
.
L’énergie mécanique ne se conserve pas.
On applique la relation ![]() pour en déduire le
travail des forces non conservatives.
pour en déduire le
travail des forces non conservatives.
On a donc ![]() .
.
D’où ![]() .
.
On ne tient pas compte de la force du poids dans le calcul du travail des forces non conservatives car le poids est une force conservative.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








