Phénomène d'interférences des ondes
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
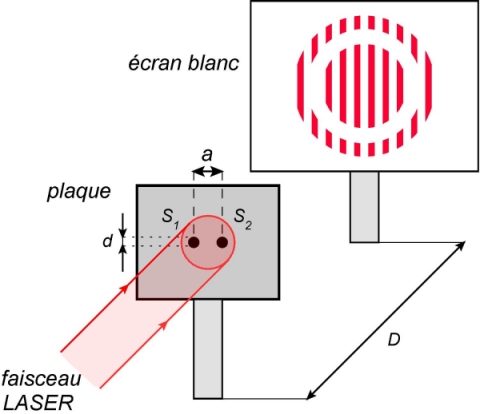

Sur l’écran, on obtient une figure de diffraction, sous la forme d’un disque, comme observé dans la fiche "diffraction".
Par contre, la nouveauté est l’apparition d’une alternance de franges sombres et brillantes. Elles sont selon un axe perpendiculaire à
Cette manipulation vient de nous montrer le phénomène d’interférences d’ondes lumineuses. L’expérience est nommée "expérience des trous de Young", en référence à Thomas Young (1773-1829) qui découvrit le phénomène en 1803.
Pour la suite, nous raisonnerons avec le schéma ci-dessous :
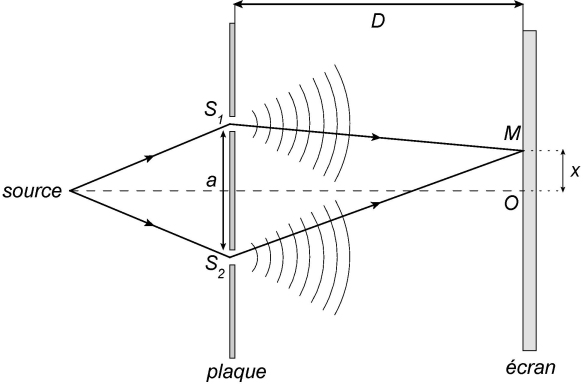
Les ondes issues de la source se propagent jusqu’aux deux trous. Au niveau de chacun d’eux, l’onde passant à travers est diffractée. Pour la partie du schéma à droite de la plaque, les trous
En O, les ondes issues des deux trous sont aussi en phase car les distances
En se décalant sur l’écran d’une longueur x par rapport à O, parallèlement à l’axe
En M, les ondes peuvent présenter un déphasage entre elles. Leur sommation donne divers résultats, selon la valeur de
• Si
• Si
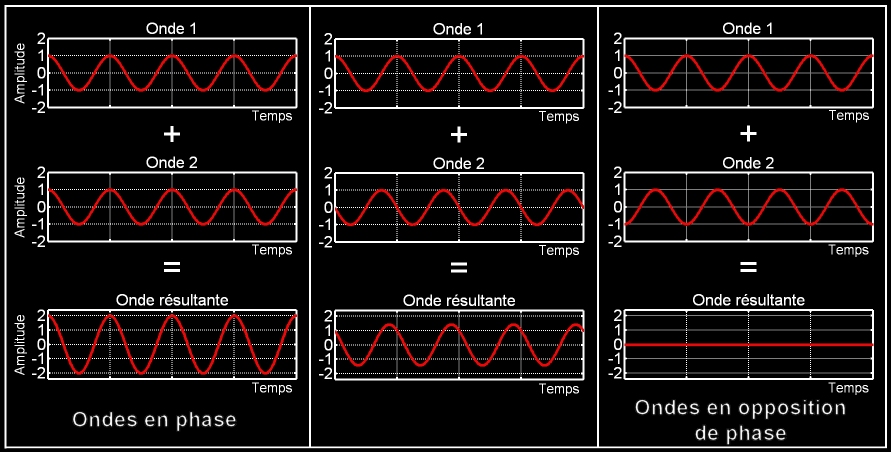
Lorsque
→ Pour une frange brillante,
→ En se décalant d’une longueur i (l’interfrange), on est sur la frange brillante suivante, et
Toutes les longueurs citées s’expriment en mètre.
Remarque : les expériences décrites sont effectuées dans l’air. Dans un autre milieu, il faudrait prendre en compte son indice optique pour le calcul de
• Avoir même fréquence. On dit alors que les sources sont synchrones.
• Etre cohérentes, c'est-à-dire avoir un déphasage constant entre elles à tout instant, en un point donné.
Par exemple, deux émetteurs ultrasonores connectés au même générateur basse fréquence (GBF) peuvent être qualifiés de sources cohérentes.
La condition de cohérence n’est pas évidente pour les ondes lumineuses. En effet, les sources lumineuses classiques n’émettent pas l’onde électromagnétique en continu, mais sous la forme de trains d’ondes (ondes générées pendant un laps de temps très court), dont la phase varie d’un train d’ondes à l’autre. Ils correspondent d’ailleurs aux photons (voir fiche "dualité onde-corpuscule").
Deux sources lumineuses comme des phares de voiture, ou deux points distincts d’une source lumineuse étendue, sont incohérentes. Cela se manifeste par deux ondes dont le déphasage entre elles est aléatoire : si à un instant les interférences sont constructives, elles peuvent être destructives en un même endroit l’instant d’après. Les interférences ne sont pas observables pour deux sources incohérentes, car il y a brouillage.
Les trous de Young permettent de « fabriquer » deux sources identiques et cohérentes en « divisant » un faisceau lumineux en deux. L’expérience de Young utilisait la lumière solaire. Actuellement, des lasers donnent de très bons résultats, car ils fournissent un faisceau de lumière cohérente (voir fiche dédiée au laser).

Le phénomène est observé avec des bulles de savon, ou avec un film d’huile sur une flaque d’eau. Une application pratique est la photoélasticimétrie, où la combinaison des interférences avec un autre phénomène physique (biréfringence) permet de visualiser les efforts mécaniques subis par une pièce, sous la forme d’un dégradé de couleurs !
→ L’astrophysique utilise l’interférométrie d’ondes électromagnétiques visibles ou dans le domaine radio. D’autre part, les projets LIGO américain et VIRGO franco-italien sont deux interféromètres géants (plusieurs kilomètres) dont le but est de détecter des ondes gravitationnelles, prédites par la théorie de la relativité générale d’Einstein.
Dans l’expérience des trous de Young, deux trous éclairés par une radiation de longueur d’onde
• Si
• Si
L’interfrange (noté i) entre deux franges brillantes consécutives est constant dans ce montage.
En lumière blanche, les motifs d’interférences se présentent sous la forme d’un dégradé de couleurs (couleurs interférentielles).
Les interférences sont utilisées avec les ondes lumineuses ou acoustiques, dans divers domaines : mesure, astrophysique, télédétection, etc.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








