Postulat d'Einstein sur l'invariance de la célérité de la lumière dans le vide : la relativité restreinte
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Si A va dans le sens contraire du tapis, alors B voit se déplacer A avec une vitesse
C’est la loi de composition des vitesses ou loi d’additivité des vitesses.
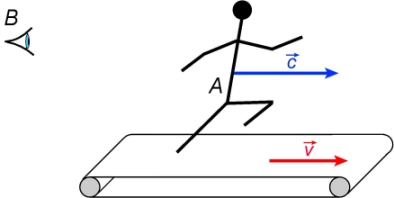
Après, on peut se demander ce qu’il se passe dans le cas de la lumière : y a-t-il additivité entre la vitesse d’une source lumineuse et la célérité de la lumière émise ? Les photons émis par les phares d’un véhicule vont-ils plus vite quand la voiture roule ?
La célérité de la lumière est forte dans le vide (
Il comprit que puisque la Terre tournait sur elle-même et autour du Soleil, alors la vitesse relative entre un point de la surface terrestre et une étoile observée devait varier au cours de la journée et au cours de l’année.
Dans l’hypothèse d’Arago, ce mouvement relatif devrait influencer la célérité de la lumière perçue sur Terre.
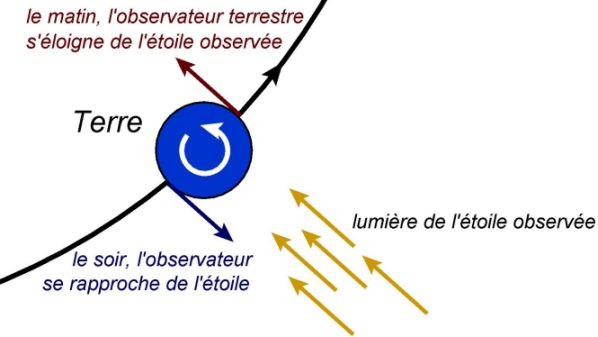
Ainsi, si la lumière de l’étoile nous parvenait avec des célérités différentes entre deux mesures, alors les spectres obtenus avec le prisme devraient être différents (plus ou moins larges). En effet, l’angle de déviation d’une radiation par un prisme dépend de l’indice optique correspondant ; l’indice optique est lié à la célérité de la lumière qui traverse le prisme.
Or, il n’observa aucune différence de largeur des spectres obtenus, pour une même étoile, lors de divers relevés (matin, soir par exemple).
L’éther était vu comme un référentiel absolu, dans lequel la lumière se propagerait avec une célérité fixe.
En supposant que l’éther soit immobile par rapport au Soleil, et comme la Terre tourne autour du Soleil, la vitesse de la Terre par rapport à l’éther devrait varier au cours de l’année terrestre. En conséquence la célérité c de la lumière devrait donc varier dans le référentiel terrestre. La vitesse orbitale de la Terre (30 km/s) est faible devant celle de la lumière, ce qui fait que cette éventuelle variation pourrait aisément passer inaperçue.
En 1887, Michelson et Morley proposèrent de la mettre en évidence avec un interféromètre :
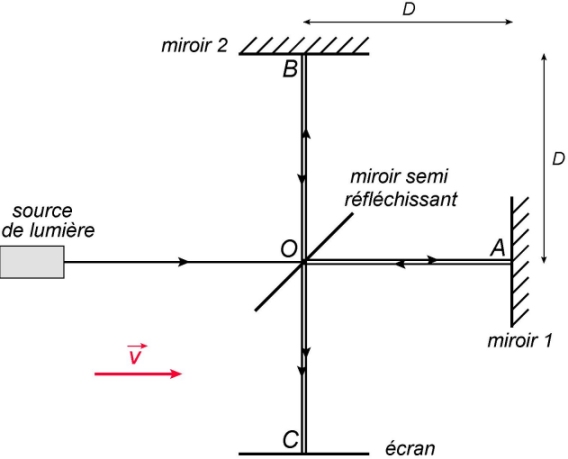
Une source monochromatique envoie un faisceau de lumière sur un miroir semi-réfléchissant. En O, une part de la lumière va vers le miroir 1, et l’autre part vers le miroir 2. Les deux miroirs réfléchissent la lumière qui repart en O. La lumière est alors captée en C sur un écran, où l’on observe des interférences (voir fiche dédiée).
On suppose que la Terre se déplace avec une vitesse
→ Le temps mis par la lumière pour faire un aller-retour entre O et le miroir 1 est
→ Le temps mis par la lumière pour faire un aller retour entre O et B est
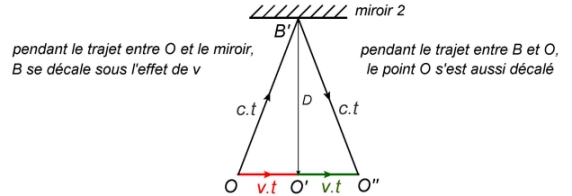
Dans le triangle rectangle
→
Or, l’état d’interférence n’a pas varié (frange brillante). Michelson et Morley n’avaient pas pour objectif de remettre en cause la théorie de l’éther. En conséquence, leur manipulation fut considérée comme un échec...
En 1905, Albert Einstein (1879-1955), s’inspirant des travaux de Lorentz et Poincaré, établit alors la théorie de la relativité restreinte. Dans le cadre de cette théorie, un postulat important est :
« La célérité de la lumière dans le vide est constante dans tout référentiel galiléen. »
Un référentiel galiléen est un référentiel dans lequel s’appliquent les lois de Newton. Cela se manifeste par le fait que si un objet n’est soumis à aucune force (ou si elles se compensent), alors sa trajectoire est rectiligne dans le référentiel galiléen. Si l’objet est immobile, il le reste. Le référentiel géocentrique (lié au Soleil) est considéré comme galiléen. Un référentiel en translation uniforme par rapport à un galiléen est lui aussi galiléen. Le référentiel terrestre est galiléen (pendant des temps courts). Un référentiel accélérant par rapport à un galiléen et/ou qui tourne sur lui-même n’est pas galiléen.
Pour en revenir à la théorie d’Einstein, la notion d’éther n’est pas prise en compte dans son modèle. En fait, Einstein considère l’éther inutile pour décrire la propagation de la lumière. Cela contredit alors le principe de référentiel absolu, et met en doute l’existence de l’éther.
Il alla plus loin, en indiquant que les lois de la physique (et pas seulement la célérité de la lumière) sont les mêmes dans tout référentiel galiléen. Comme on le verra dans la fiche suivante, la théorie de la relativité restreinte se manifeste également par un abandon du temps absolu, au profit du temps relatif.
Remarques :
• La théorie est nommée relativité restreinte, car elle est restreinte aux référentiels galiléens. Einstein développa une théorie englobant les autres référentiels. Cette théorie fut alors nommée théorie de la relativité générale.
• Des manipulations visant à vérifier la théorie d’Einstein ont eu lieu après 1905. On peut citer l’expérience menée au C.E.R.N. en 1964, par Alväger, Farley, Kjellman et Wallin. L’idée fut de mesurer la célérité de photons
• En 1905, Albert Einstein énonça la théorie de la relativité restreinte. Dans cette théorie, un postulat important est que :« La célérité de la lumière dans le vide est invariante dans tout référentiel galiléen. »
Cette théorie a remis en cause certains modèles basés sur un référentiel absolu lié à l’éther.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








