Lycée > Terminale > Physique Chimie > Constante d'Avogadro, évaluer des ordres de grandeurs

Constante d'Avogadro, évaluer des ordres de grandeurs

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectifs

Rappeler ce qu’est le nombre d’Avogadro. Montrer que cette constante établit un lien entre le monde microscopique et macroscopique. Voir comment le nombre d’Avogadro intervient dans d’autres constantes physiques. Décrire deux méthodes expérimentales pour estimer le nombre d’Avogadro.

1. La constante d'Avogadro

Notamment en chimie, on est souvent amené à étudier des phénomènes observables macroscopiquement : combustion, précipitation, dégagement gazeux, etc. Or, ces phénomènes sont directement reliés à des réactions chimiques, qui se produisent ainsi à l’échelle de la molécule. Quand on se limite à une analyse qualitative (changement de couleur d’une solution), cela ne pose pas de difficultés. Mais, dès que l’on souhaite faire des calculs, il faut « compter les molécules ». Il y a ainsi la nécessité d’établir un lien entre le monde macroscopique et microscopique.

Quand on manipule des grands nombres, on les groupe en « paquets » : millions, milliards, … et/ou on emploie des exposants. La solution retenue en chimie est de considérer la mole, c'est-à-dire une collection d’« objets » identiques (molécules, atomes, …). Le nombre d’entités dans une mole est donnée par le nombre (ou constante) d’Avogadro

.

La mole a été définie comme le nombre d’atomes de carbone contenus dans 12 grammes de carbone 12 pur. De part cette définition,

n’est pas connue de manière exacte. Sa valeur approchée actuellement retenue est environ de :

l’unité

devant être comprise comme « nombre d’entités par mole ». L’incertitude relative est de

(plus ou moins cette valeur).

De part le nombre colossal que représente

, c'est-à-dire environ 602 214,129 milliards de milliards, il est illusoire (et même inutile) d’essayer de connaître le nombre d’Avogadro avec une précision absolue, à l’unité près. D’ailleurs, si on pouvait compter les atomes un par un, à un rythme de un par seconde, il faudrait

années pour recenser une seule mole d’atomes.

L’Univers a environ

…

2. Lien entre le nombre d'Avogadro et d'autres constantes physiques

On connaît les formules basées sur l’utilisation de la mole : nombre de mole

(M est la masse molaire), concentration molaire

. Or, la mole ou

interviennent à d’autres occasions.

a. La constante des gaz parfaits

Amedeo Avogadro (1776-1856) émis l’hypothèse en 1811 que deux volumes égaux de gaz, pris dans les mêmes conditions de températures et pression, renferment autant de molécules de gaz, quelle que soit la nature de ces derniers (

).

Cela a donné la loi d’Avogadro, aussi connue sous le nom de loi des gaz parfaits :

La pression P est en Pa, le volume V en

, le nombre de moles n en mol, la température T en Kelvin et R est la constante des gaz parfaits.

Cette constante résulte de la relation :

où

est la constante de Boltzmann, qui est utilisée pour faire le lien entre la température et l’énergie interne d’un système (voir fiche dédiée).

La loi des gaz parfaits est une parfaite illustration du lien entre microscopique et macroscopique, car cette loi rend compte du comportement des molécules d’un gaz. En effet, les molécules, par leur agitation désordonnée, donnent lieu à la température. D’autre part, par leurs chocs répétés contre les obstacles (parois), cela donne alors la pression.

Remarque : la loi des gaz parfaits peut être vue comme une généralisation de la formule

, où

est le volume molaire. Dans les conditions normales de température et pression, respectivement

, le volume molaire vaut :

b. La constante de Faraday

La constante de Faraday est par définition la charge électrique d’une mole d’électrons, en valeur absolue. Ce nombre se note conventionnellement

. On a :

Le e est la charge élémentaire, c'est-à-dire la charge du proton, ou celle de l’électron en valeur absolue.

, ce qui donne

.

La constante de Faraday est utilisée par exemple en électrochimie, pour étudier le fonctionnement d’une pile, d’un accumulateur électrique, d’un électrolyseur (cours 1ère S). En effet, il permet de faire le lien entre les formules électriques et les relations de chimie.

Plus précisément,

donne la charge électrique (en C) comme le produit du courant électrique I (en A) par le temps t (en s). Q s’exprime aussi comme

, où

est le nombre de moles d’électrons qui a transité dans le circuit électrique. Cette quantité d’électrons est alors mise en relation avec les demi-équations chimiques qui régissent le fonctionnement de l’appareil étudié. Par exemple pour une pile Daniell :

On peut alors estimer la quantité (puis la masse) de cuivre formé ou de zinc consommé au niveau des électrodes de la pile.

c. Unité de masse atomique

L’unité de masse atomique (appelée aussi unité de masse atomique unifiée) est par définition la masse de 1/12ème de la masse d’un atome de carbone 12, mesurée dans des conditions standards (au repos, atome non lié). Comme

atomes de carbone 12 ont par définition une masse de 12 grammes, on en déduit que :

c'est-à-dire

Ici, la constante d’Avogadro fait le lien entre la masse d’un échantillon macroscopique et la masse des atomes qui le constituent.

L’unité de masse atomique est utile pour estimer la masse d’atomes/molécules, mais est aussi utilisée en physique nucléaire. En effet, la masse d’un électron est presque 2000 fois plus faible que celle d’un nucléon (proton ou neutron). La masse d’un noyau est ainsi considérée égale à celle de l’atome correspondant, et peut s'exprimer en u.

En physique nucléaire, il est courant de « convertir » une masse m en énergie

, en utilisant la relation d’Einstein

, où c est la célérité de la lumière dans le vide. Le Joule n’étant pas adapté à la physique du noyau, on fait appel au MeV (méga-électronvolt), multiple de l’électronvolt.

donc

. Ainsi, on a la relation masse/énergie

environ.

3. Comment déterminer le nombre d'Avogadro expérimentalement ?

Certaines constantes physiques sont définies de façon exacte, comme la célérité de la lumière dans le vide

, puisqu’elle sert à définir le mètre (distance parcourue en

). Mais, la plupart des constantes physiques ne sont connues que par des valeurs approchées. Si pour un élève de lycée la valeur de ces constantes semble « figée », il n’en est rien. Cela ne veut pas dire que les constantes physiques fondamentales varient, mais que la connaissance que l’on a d’elles s’affine.

Des équipes de scientifiques ont pour objectif d’améliorer la précision de telle ou telle constante. Les progrès technologiques, mais aussi l’ingéniosité des expérimentateurs, permettent ces avancées. Une fois les résultats validés par la communauté scientifique, ils sont publiés. Le site ci-après rend accessible les dernières mises à jour :
http://physics.nist.gov/cuu/Constants/.

Il en est de même pour le nombre d’Avogadro dont la valeur approchée a été vue au 1. D’ailleurs, ce fut le scientifique Français Jean Perrin (1870-1942) qui nomma cette constante en l’honneur d’Avogadro. De plus, il proposa en 1908 une estimation correcte de

par différentes méthodes (étude du mouvement Brownien, etc.). Ci-après deux autres méthodes récentes :

→ Une technique (Bower et Davis en 1975) fut de trouver la valeur de la constante de Faraday, pour ensuite en déduire une valeur du nombre d’Avogadro, voir 2.b. Pour cela, il fut utilisé un montage d’électrolyse. D’un côté, il fut mesuré la charge électrique qui a transité dans le circuit. De l’autre, il fut mesuré la variation de la masse d’une anode en argent.

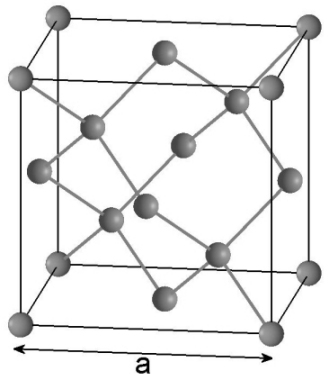
→ Un programme nommé the International Avogadro Coordination confectionna des boules de silicium monocristal, les plus pures possible. Les opérateurs ont fait en sorte que la masse d’une boule soit de un kilogramme, avec une imprécision de seulement quelques microgrammes. Ensuite, des mesures furent effectuées sur la boule, pour trouver notamment sa masse volumique. Par diffractométrie de rayons X, il fut déterminé le paramètre de maille a du cristal de silicium (arrête du cube), voir schéma ci-dessous (structure de type diamant).

Cela a permis de connaître le nombre d’atomes de silicium dans un certain volume. Avec la masse molaire du silicium, il fut possible de remonter à

(travaux publiés en Janvier 2011).

L'essentiel

La constante d’Avogadro

(ou nombre d’Avogadro) désigne le nombre d’entités contenues dans une mole. Actuellement, sa valeur est estimée à

. C’est un nombre colossal, difficilement concevable.

est une constante physique faisant le lien entre le monde microscopique et le monde macroscopique. La constante des gaz parfaits R, la constante de Faraday

et l’unité de masse atomique u sont définies grâce au nombre d’Avogadro.

Cette constante a été nommée de la sorte par Jean Perrin, en hommage aux travaux d’Amedeo Avogadro. Perrin a d’ailleurs proposé des méthodes afin d’estimer