Une conséquence de la relativité restreinte : caractère relatif du temps, dilatation des durées

Considérons deux miroirs parallèles, distants d'une longueur L. Un photon (particule de lumière) se déplace de l’un vers l’autre, à la vitesse , en faisant des allers-retours.

Dans le référentiel (R’), lié aux miroirs et supposé galiléen, le mouvement perpétuel du photon constitue une « horloge de lumière ». En effet, la durée requise pour aller d’un miroir à l’autre est constante. Le photon fait des allers-retours entre les deux miroirs.


Considérons que le montage se déplace à vitesse constante v par rapport à un observateur immobile lié à un référentiel (R). La trajectoire du photon vue par l’observateur se présente sous la forme de lignes brisées.


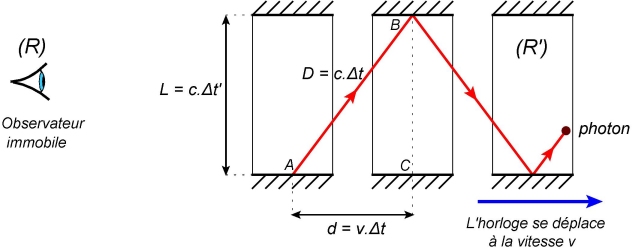
Comme (R) et (R’) sont en translation uniforme l’un par rapport à l’autre, si l’un est galiléen (ce que nous supposerons), l’autre l’est aussi. Ainsi, dans le référentiel galiléen (R), le photon se déplace à la vitesse c. Dans (R), le photon a une distance D à parcourir, plus longue que L. Le temps qu’il met pour aller d’un miroir à l’autre est ainsi plus grand dans (R) que dans (R’). Ce phénomène est la dilatation des durées.


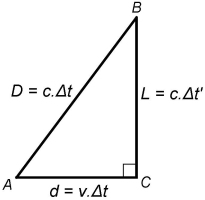
Calcul : D’après le théorème de Pythagore, on écrit que .

Comme , et , on a :

, ce qui donne , puis , et alors ou

Donc : 


Remarque : Nous avons étudié le cas où le photon se propage selon un axe perpendiculaire au sens de déplacement de (R’). En effet, si le mouvement s’était effectué selon , il aurait fallu prendre en compte une autre conséquence de la relativité restreinte : la compression des longueurs. Nous n’en parlerons pas cette année, mais nous précisons juste qu’elle n’agit que selon la direction de .

On peut généraliser l'expérience précédente à deux référentiels galiléens (R) et (R’) en translation uniforme l’un par rapport à l’autre, à la vitesse :


En relativité restreinte, le temps n’est pas absolu comme en mécanique non relativiste, mais il est relatif au référentiel dans lequel on le mesure. Ainsi, un événement étudié dans un référentiel est indiqué par , c'est-à-dire par la date et le lieu mesurés dans le repère associé au référentiel.

On appelle temps propre un intervalle de temps mesuré dans un référentiel entre deux événements qui se produisent en un même lieu dans le référentiel. est ainsi le temps propre mesuré dans (R’).

Cet intervalle de temps correspond à pour un observateur lié au référentiel fixe (R). Ces deux intervalles de temps sont reliés par la relation établie au 1 :

, noté aussi avec , nommé facteur de Lorentz

est nommé temps impropre, dans le sens où c’est un temps mesuré dans un référentiel où les deux événements ne se produisent pas au même endroit. Dans la pratique, c’est le temps mesuré dans le référentiel fixe, pour lequel l'objet observé se déplace.

Propriétés :
→ Comme , on a , donc et . Ainsi, . En conséquence, on a toujours . Pour un observateur dans le référentiel fixe, le temps paraît s’écouler plus lentement dans le référentiel en mouvement que dans son référentiel fixe.

→ Comme la formule utilise un terme en , le sens de la vitesse v n’a pas importance : on a le même effet si (R’) se rapproche ou s’éloigne de (R). C’est une différence avec l’effet Doppler-Fizeau (voir fiche dédiée).

→ On admet que les effets relativistes commencent à être perceptibles dès que v atteint 10 % de c. Pour cette valeur, on a : variation de 0,5 % entre temps propre et impropre.

→ En relativité restreinte, il n’y a pas de référentiel absolu, la vitesse entre les deux référentiels galiléens est relative (l’un par rapport à l’autre). Ainsi, on peut considérer aussi que (R’) est fixe et que (R) se déplace. Dans (R’), le temps semble s’écouler normalement pour un observateur dans (R’). Par contre, le temps semble s’écouler plus lentement dans (R) pour l’observateur lié à (R’). En clair, chaque observateur a l’impression que le temps s’écoule plus lentement dans le référentiel en mouvement par rapport à lui que dans son propre référentiel !

→ Imaginons que le référentiel (R’) soit celui d’une particule voyageant à la vitesse v par rapport à (R). Autrement dit, la particule est fixe dans (R’). Puisque , la relation n’est calculable que si donc si . Ainsi, une particule ne peut pas avoir une vitesse supérieure à c par rapport à un observateur immobile dans un référentiel galiléen.

Dans le cas où , : on ne voit pas « vieillir » une particule voyageant avec la célérité de la lumière. Seules les particules de masse nulle ont cette possibilité dans la pratique. Notons toutefois que lier un référentiel à un photon est un non-sens physique, car la célérité de la lumière est constante dans tout référentiel galiléen.

→ Pour appliquer la formule de dilatation des durées, il faut que les deux référentiels soient galiléens. Il est ainsi important que le référentiel en mouvement évolue à vitesse constante par rapport au référentiel fixe. Sinon, les résultats seront faux et même aberrants.

Durée de vie des muons

Dans la haute atmosphère, à environ 50 km d’altitude, des particules de hautes énergies réagissent avec les atomes présents. Cela donne naissance à des muons. Ces particules sont de la même famille que les électrons (les leptons), mais sont 200 fois plus lourdes et ont une durée de vie de . En voyageant avec une vitesse proche de celle de la lumière, on pourrait s’attendre à ce qu’elles parcourent en une distance d telle que , et ainsi .

Ces particules ne devraient pas être détectables à la surface terrestre, 50 km plus bas. Or, c’est le cas. En effet, même si la durée de vie du muon est bien de dans le référentiel où le muon est au repos, elle est plus forte dans le référentiel terrestre par dilatation des durées.

Naturellement, ce phénomène d’allongement de la durée de vie de particules instables a été également observé auprès des accélérateurs de particules.

Horloges atomiques embarquées : expérience de Hafele–Keating

En 1971, afin de vérifier le phénomène de dilatation des durées, des horloges atomiques furent embarquées dans deux avions pour faire deux fois le tour du monde, un avion vers l’est, l’autre vers l’ouest. Une autre horloge resta sur Terre. Il fut constaté un décalage des horloges, en accord avec la théorie de la relativité restreinte, même si la relativité générale est aussi à prendre en compte dans cette expérience.

Le GPS

Le Global Positioning System est un système de guidage, utilisé par exemple par les automobilistes. Il consiste en un ensemble de satellites qui transmettent en continu des signaux par ondes électromagnétiques à la surface terrestre, indiquant leur position, ainsi que le temps mesuré par l’horloge atomique du satellite. Quand un récepteur GPS capte ces signaux, il compare le temps du satellite à sa propre horloge, afin de trouver la durée qu’il a fallu au signal pour parvenir jusqu’à lui. Comme le signal voyage à la célérité de la lumière, le récepteur calcule sa distance par rapport au satellite. Avec 4 satellites GPS, le récepteur détermine sa position : longitude, latitude, altitude.

Cependant, de part sa vitesse orbitale, le satellite se déplace par rapport au récepteur. Le phénomène de dilatation des durées intervient, pouvant fausser les mesures. D’autre part, la théorie de la relativité générale précise que le temps ne s’écoule pas à la même vitesse suivant que l’on soit proche d’un objet massif (à la surface terrestre) ou pas (en orbite), ce qui rajoute une source d’erreur supplémentaire. Il est ainsi nécessaire d’opérer des corrections relativistes. Sans ces ajustements, le décalage temporel entre les satellites et le récepteur s’accentuerait de quelques par jour, ce qui causerait une erreur de localisation qui grandirait de plusieurs kilomètres par jour …