L'effet Doppler
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Prenons l'exemple d'un klaxon :
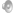
Quand la voiture se rapproche, le son paraît plus aigu que le son perçu par le conducteur. Quand elle s’éloigne, le son paraît plus grave. C’est une manifestation de l’effet Doppler.
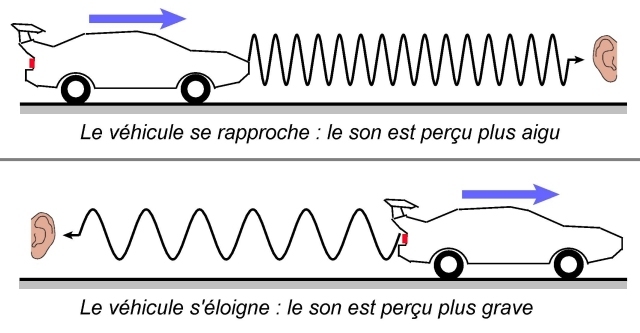
On procède à une analyse de l’extrait sonore (voir fiche analyse spectrale), afin de voir comment les fréquences varient pour l’observateur immobile.
Les sons captés comportent de nombreuses harmoniques ; une parmi elles a été repassée en rouge sur le graphe. Durant la phase d’approche, la fréquence mesurée par l’observateur est constante. Idem avec la phase où la voiture s’éloigne. Cette observation est vraie parce que la vitesse du véhicule est constante dans le référentiel de l’observateur.
Comme
,
une augmentation de la longueur d’onde
s’accompagne d’une diminution de la
fréquence f, et
inversement.Dans le cadre des ondes acoustiques, la description s’applique bien aux avions de chasse :
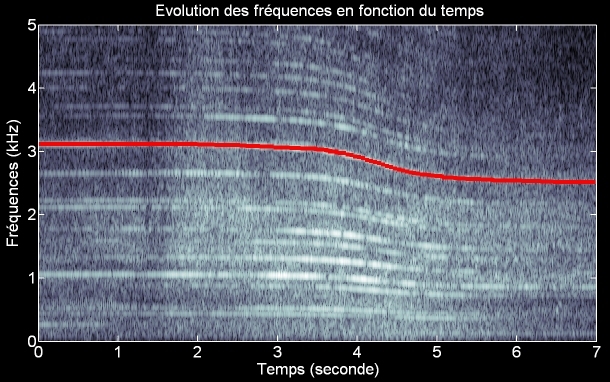
• Quand un mobile se déplace aussi vite que le son qu’il émet (cas n°3), le son n’est pas émis en avant du mobile, car celui-ci « rattrape » son propre son.
• Quand le mobile va plus vite que le son (cas n°4), les sons émis sont confinés dans un cône à l’arrière, nommé cône de Mach, d’autant plus étroit que le mobile va vite.
Le cas n°2 (
)
correspond à un effet Doppler sonore tel
que nous l’utiliserons.
(en Hz), de période 
(en s), de longueur d’onde 
(en m). L’onde a une
célérité c (en m/s)
dans son milieu de propagation. Soit un récepteur,
qui capte l’onde avec une fréquence
,
une période 
et une longueur d’onde 
.1) source en mouvement avec une vitesse
, récepteur
fixe.L’effet du déplacement de la source n’affecte pas la célérité de l’onde, mais contracte/dilate la longueur d’onde
,
et par extension agit sur la fréquence 
(voir cas n°2 du 1.b) : 
,
avec + si la source s’éloigne du
récepteur, et un – si la source se
rapproche.
,
et 
.Ainsi, on a
ou 
, Et finalement :
Si la source s’éloigne du récepteur (signe +),
.Si la source se rapproche du récepteur (signe –),
.2) source fixe, récepteur en mouvement avec une vitesse
.Comme l’onde a une célérité c dans son milieu de propagation, le déplacement du récepteur fait que celui-ci « voit » l’onde sonore se propager avec une célérité
,
avec un + si le récepteur va vers la source, et un
– si il s’en éloigne. La longueur
d’onde 
est « vue » de manière identique, mais
la « modification » de la
célérité a une influence sur
: 
,
ainsi 
.Comme
ou 
,
Donc :
Si le récepteur se rapproche de la source (signe +),
.Si le récepteur s’éloigne de la source (signe –),
.3) la source et le récepteur se déplacent par rapport au milieu de propagation de l’onde, le long d’un même axe, respectivement avec des vitesses
et 
(référentiel terrestre).Dans ce cas de figure, 1) et 2) interviennent en même temps, et :
Signe + au numérateur : le récepteur se dirige vers la source.
Signe – au numérateur : le récepteur va à l’opposé de la source.
Signe + au dénominateur : la source va à l’opposé du récepteur.
Signe – au dénominateur : la source se dirige vers le récepteur.
C’est une vitesse algébrique :
si éloignement,
si rapprochement.et
est la
célérité de la lumière dans
le vide.Quand
, la relation peut se mettre
sous les formes suivantes :
ou 
, avec 
ou 
, avec 
On parle d’effet Doppler-Fizeau pour désigner l’effet Doppler appliqué à la lumière, en référence à Hippolyte Fizeau (1819-1896), qui, comme Christian Doppler (1803-1853), travailla sur le phénomène.
→ Médical. En médecine, « un Doppler » est un examen médical dont le but est de mesurer la vitesse d’organes (battements cardiaques) ou de fluides corporels, comme le sang.
→ Industrie. Par un procédé proche de celui utilisé en médecine, il est possible de mesurer des vitesses à distance : mesure de la vitesse d’écoulement d’un fluide dans une canalisation, etc.
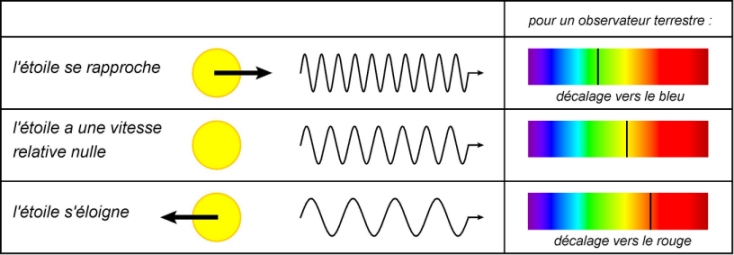
→ Astrophysique. Le spectre d’une étoile comporte des raies d’absorption atomiques, de longueurs d’onde connues
,
à vitesse d’éloignement nulle. En
comparant aux longueurs d’onde 
des raies de l’étoile observée, on en
déduit la vitesse relative de
l’étoile v par rapport à nous :
. Le signe de v indique si l’étoile
s’éloigne (+) ou se rapproche (–).
→ Pour le son, lorsqu’une source s et une récepteur r se déplacent le long d’un même axe, l’effet Doppler donne la relation :
Les v sont les vitesses (m/s) dans le référentiel terrestre, f les fréquences (Hz), et c la célérité du son (m/s).
Au numérateur, signe + quand le récepteur se dirige vers la source, – sinon.
Au dénominateur, signe + quand la source va à l’opposé du récepteur, – sinon.
→ Pour les ondes électromagnétiques, dont la lumière, l’effet Doppler-Fizeau s’écrit :
avec 
et 
avec 
v est positif s’il y a éloignement, négatif si rapprochement (grandeur algébrique).
L’effet Doppler présente diverses applications, car il permet d’estimer à distance la vitesse d’un corps (médecine, astrophysique, …).
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Fermer
Accédez gratuitement à
