Les liaisons mécaniques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Pouvoir modéliser les mouvements entre les pièces d’un mécanisme.
- Un mécanisme est un ensemble d’éléments articulés entre eux pour réaliser une fonction.
- La nature du contact entre deux solides diffère selon le type de surface en contact. Il en découle des degrés de liberté (ddl), qui indiquent les possibilités de mouvement dans l’espace de ces deux solides.
- Chaque liaison mécanique possède des caractéristiques géométriques spécifiques de surfaces de contact et donc de degrés de libertés supprimés.
Les articulations sont appelées liaisons mécaniques. Elles permettent de limiter les mouvements possibles d’un élément par rapport à un autre élément.
- En phase de conception, la modélisation des mécanismes permet de réaliser des croquis pour expliquer le mouvement des différents ensembles de pièces les uns par rapport aux autres.
- En phase d’analyse d’un mécanisme existant, la modélisation permet de comprendre rapidement le fonctionnement du mécanisme, indépendamment de la complexité des pièces.
Un système mécanique est composé de plusieurs solides qui ont une ou plusieurs surfaces de contacts entre eux.
Le tableau ci-dessous présente les différentes surfaces de contact entre deux solides et les natures de contact associées.
| Nature du contact | Surfaces de contact | |
| Ponctuel |
 sphère / plan |
|
| Linéaire | rectiligne |
 cylindre / plan |
| circulaire (ou annulaire) |
 sphère / cylindre |
|
| Surfacique | plan |
 plan / plan |
| cylindrique |
 cylindre / cylindre |
|
| sphérique |
 sphère / sphère |
|
| hélicoïdal |
 hélice / hélice |
|
| conique |
 cône / cône |
|
Si on considère deux solides n’ayant aucun contact entre eux, le nombre de mouvements indépendants possibles entre les deux solides est de six.
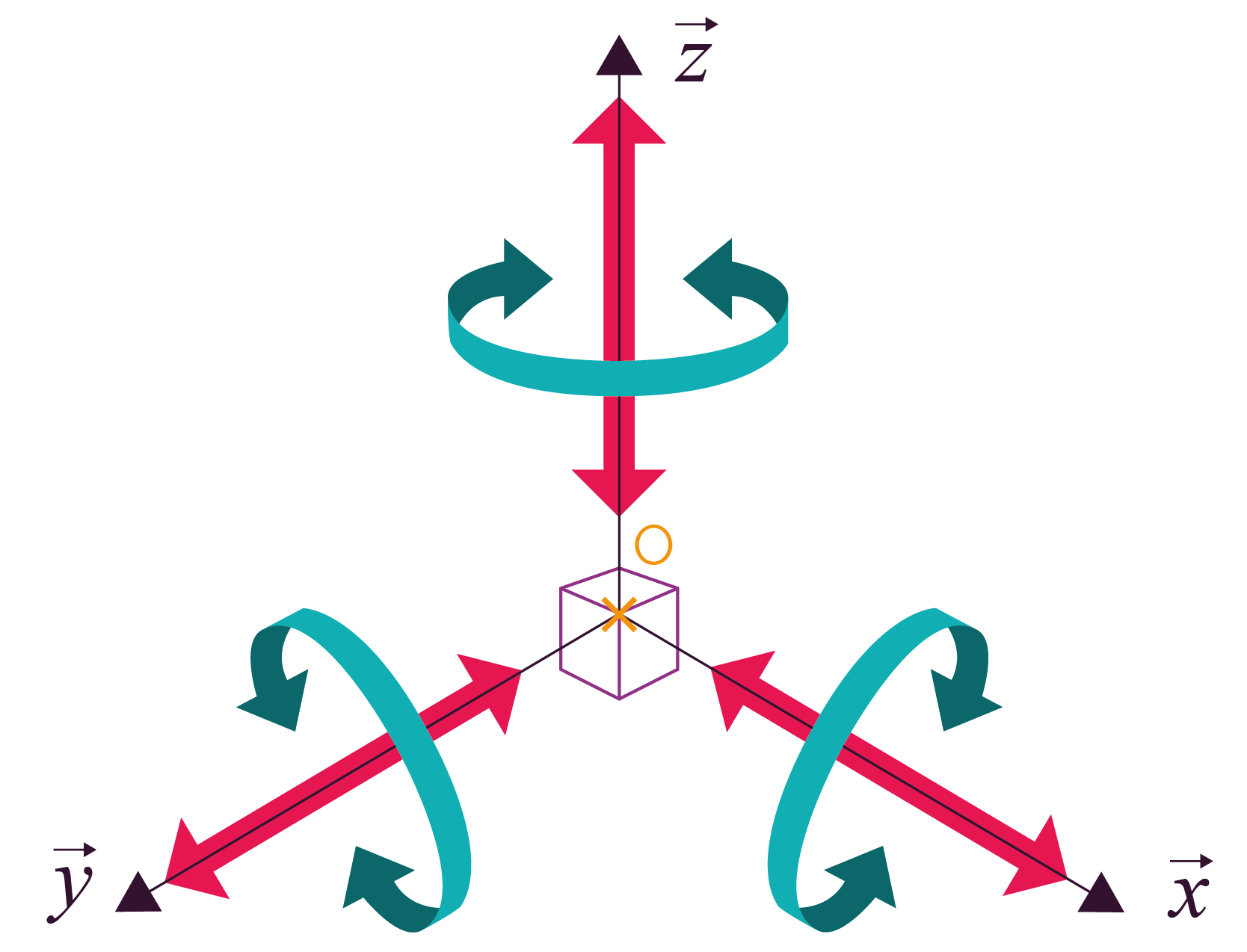
La pièce peut se déplacer :
- en translation suivant chacun des
axes
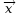 ,
, 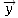 et
et 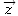 ;
;
- en rotation autour de chacun des
axes
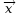 ,
, 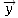 et
et 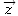 .
.
Chaque contact entre les deux pièces limite les mobilités.
Les caractéristiques géométriques de ces surfaces de contact (et donc les mobilités supprimées) permettent de définir les différentes liaisons mécaniques.
- Les degrés de liberté (ddl) d’une liaison correspondent au nombre de déplacements élémentaires indépendants qui sont autorisés par cette liaison.
- À l’inverse, les degrés de liaison correspondent au nombre de déplacement élémentaires qui sont interdits par cette liaison.
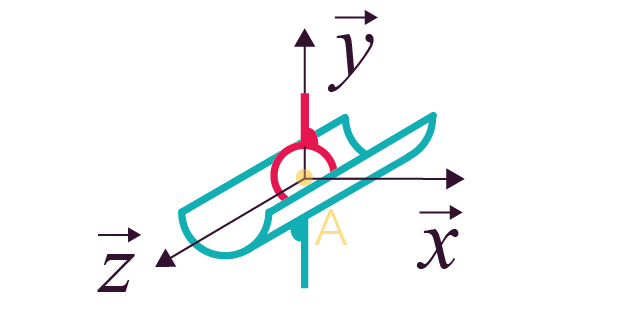
Lorsqu’un zéro est placé dans les coordonnées du torseur, cela signifie que le mouvement est impossible. Ce 0 correspond à un degré de liberté supprimé.
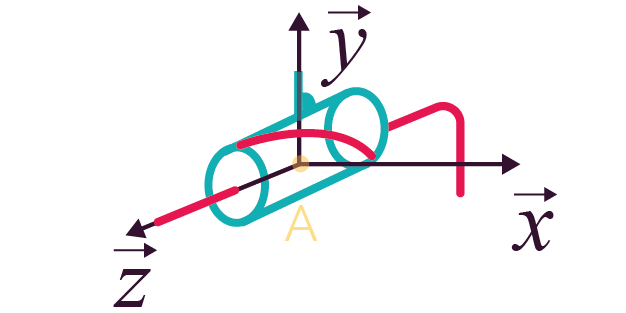
Voici le torseur cinématique entre les
pièces 1 et 2, au point de projection
A et dans le
repère de projection ![]() .
.
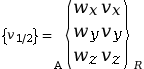
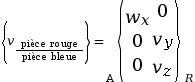 signifie qu’il y a une rotation possible
selon l’axe
signifie qu’il y a une rotation possible
selon l’axe Le tableau ci-dessous répertorie les principales liaisons mécaniques, en indiquant le nombre de degrés de liberté et le torseur cinématique associés.
| Caractérisation de la liaison | Nombre de degrés de liberté | Torseur cinématique au centre de la liaison |
Schématisations plan (orthogonale) et spatiale (en perspective) |
|
Liaison encastrement (ou liaison fixe) |
0 (0 translation et 0 rotation) |
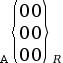
|
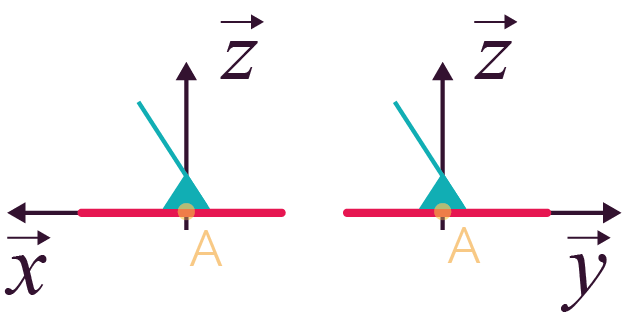 Représentation plane Représentation plane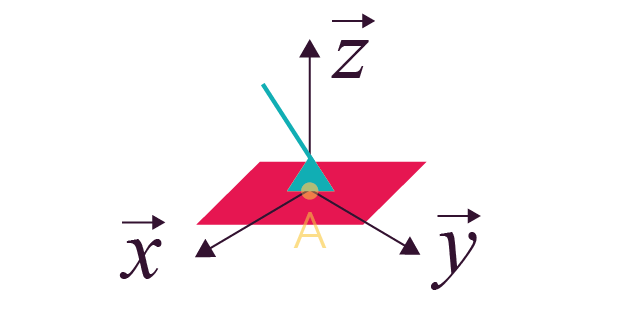 Représentation en perspective Représentation en perspective
|
|
Liaison glissière
d’axe |
1 (1 translation et 0 rotation) |
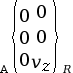
|
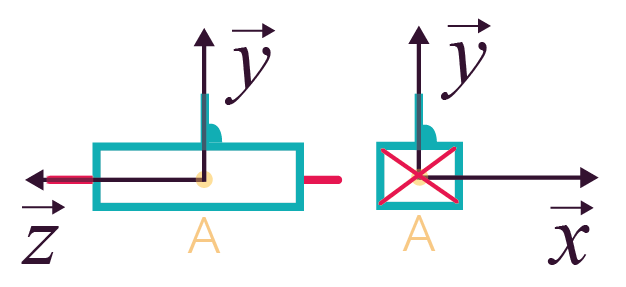 Représentation plane Représentation plane
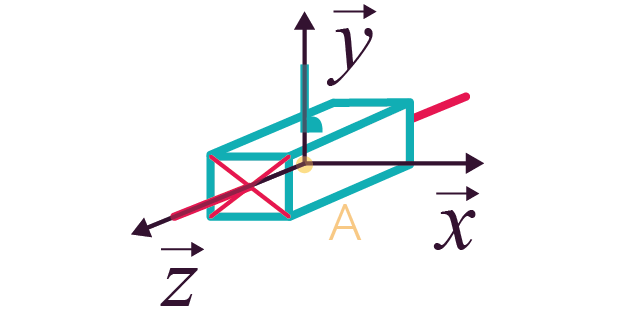 Représentation en perspective Représentation en perspective
|
|
Liaison pivot d’axe |
1 (0 translation et 1 rotation) |
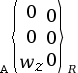
|
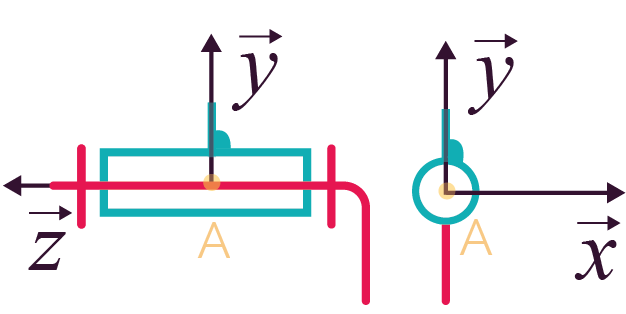 Représentation plane Représentation plane
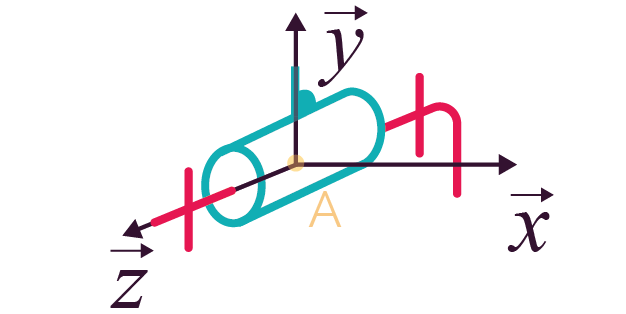 Représentation en perspective Représentation en perspective
|
|
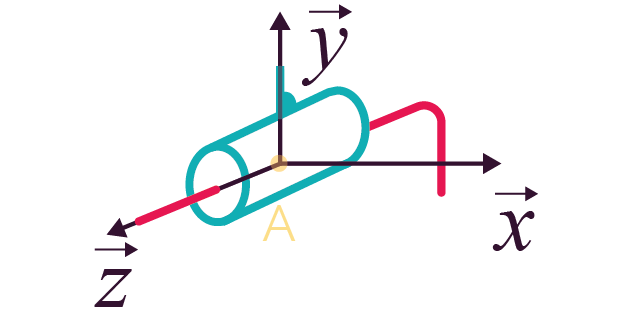
Liaison hélicoïdale
d’axe |
1 (1 translation et 1 rotation conjuguées) |
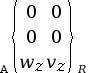
|
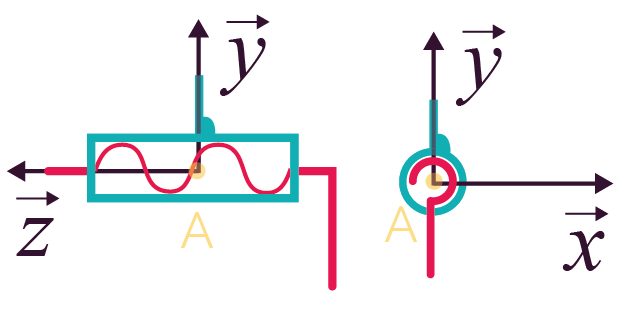 Représentation plane Représentation plane
 Représentation en perspective Représentation en perspective
|
|
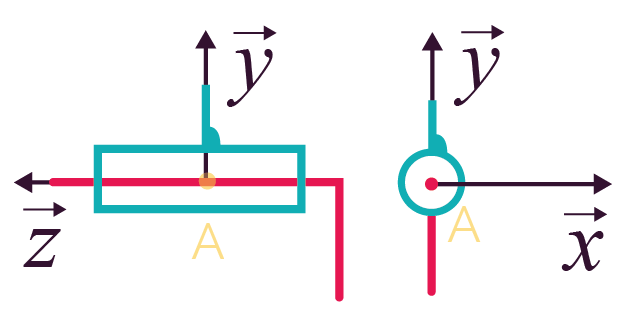
Liaison pivot-glissant
d’axe |
2 (1 translation et 1 rotation) |
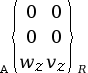
|
 Représentation plane Représentation plane
 Représentation en perspective Représentation en perspective
|
| Liaison rotule ou liaison sphérique de centre A | 3 (0 translation et 3 rotations) |
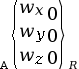
|
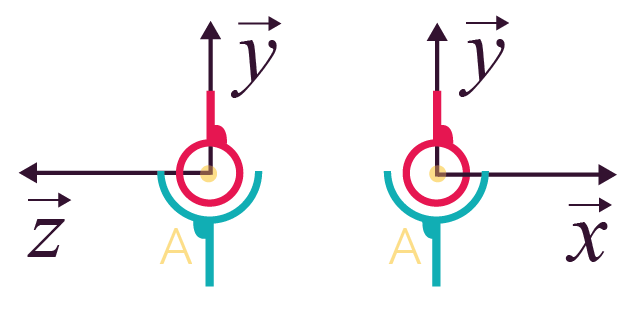 Représentation plane Représentation plane
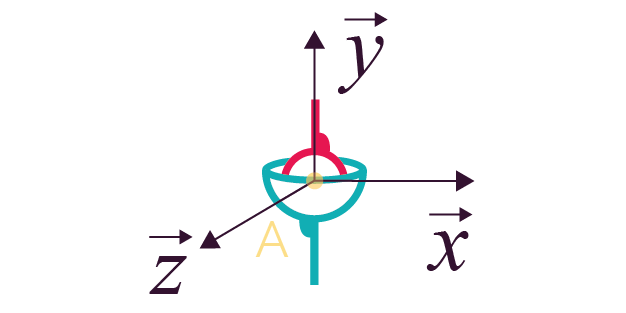 Représentation en perspective Représentation en perspective
|
|
Liaison appui plan de
normale |
3 (2 translations et 1 rotation) |
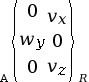
|
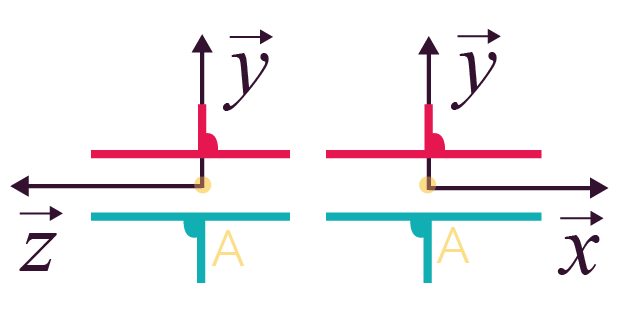 Représentation plane Représentation plane
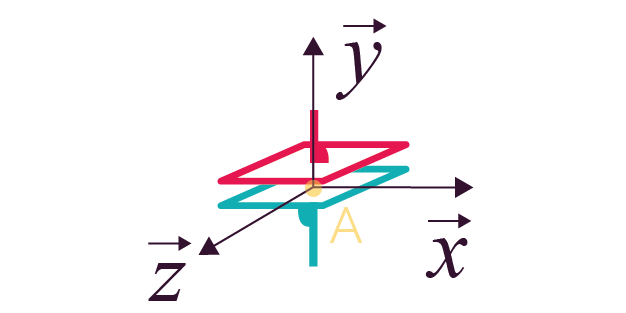 Représentation en perspective Représentation en perspective
|
|
Liaison linéaire annulaire
(sphère cylindre)
d’axe |
4 (1 translation et 3 rotations) |
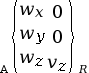
|
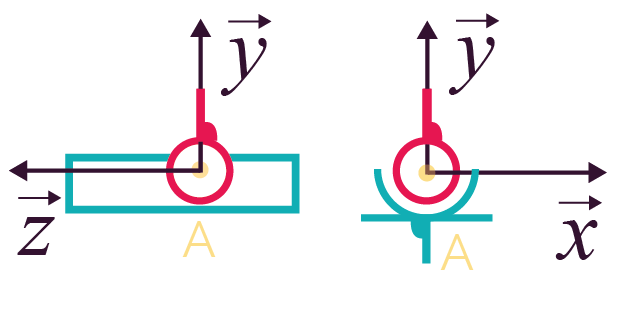 Représentation plane Représentation plane
 Représentation en perspective Représentation en perspective
|
|
Liaison linéaire rectiligne
(cylindre plan)
de normale |
4 (2 translations et 2 rotations) |
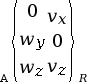
|
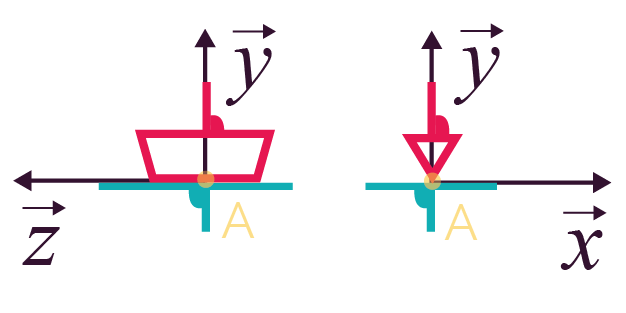 Représentation plane Représentation plane
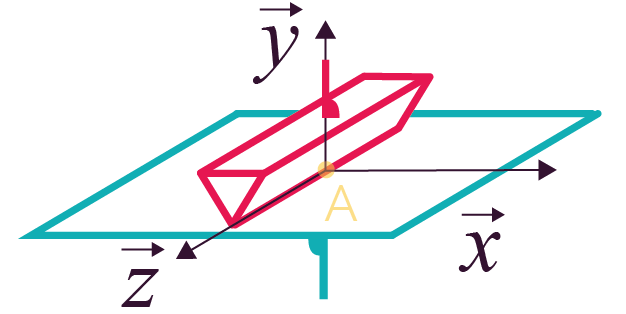 Représentation en perspective Représentation en perspective
|
|
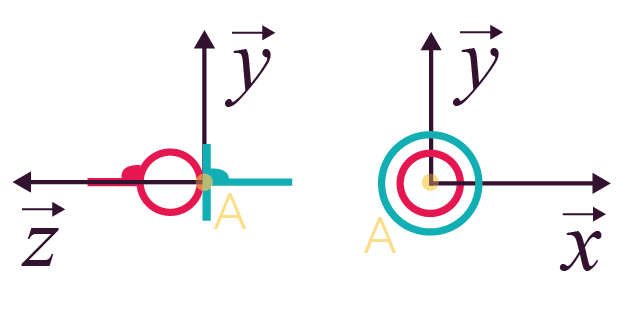
Liaison ponctuelle (sphère plan)
de normale |
5 (2 translations et 3 rotations) |
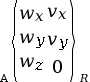
|
 Représentation plane Représentation plane
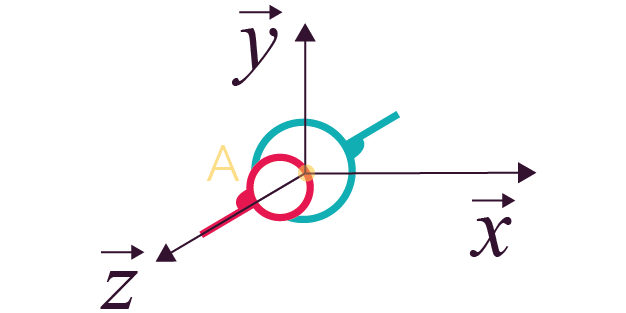 Représentation en perspective Représentation en perspective
|
Pour la liaison ponctuelle de normale
La rotation de la boule peut quant à elle se faire selon tous les axes (

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









