Lycée > Premiere > Sciences de l’ingénieur > Les transformations de mouvement

Les transformations de mouvement

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectifs

Connaitre les systèmes de transformation de mouvement.
Calculer une grandeur cinématique d’un mécanisme (rapport de transmission).
Analyser la réversibilité d’un élément de la chaine de puissance.

Points clés

La transformation du mouvement fait appel à la fonction TRANSMETTRE.
Les systèmes de transformation de mouvement permettent d’adapter le mouvement à l’utilisation visée.
Selon l’objectif recherché, les systèmes de transformation mettent en œuvre des mouvements différents, il faut donc utiliser les formules adaptées.

Pour bien comprendre

La représentation du réel
Chaines d’énergie et chaines d’information
Le couple de forces (Physique-Chimie – CAP)

1. De la fonction TRANSMETTRE au système de transformation

La fonction TRANSMETTRE permet de transmettre l’énergie reçue et agit directement sur la matière d’œuvre.

Cette fonction se trouve au bout de la chaine d’énergie.

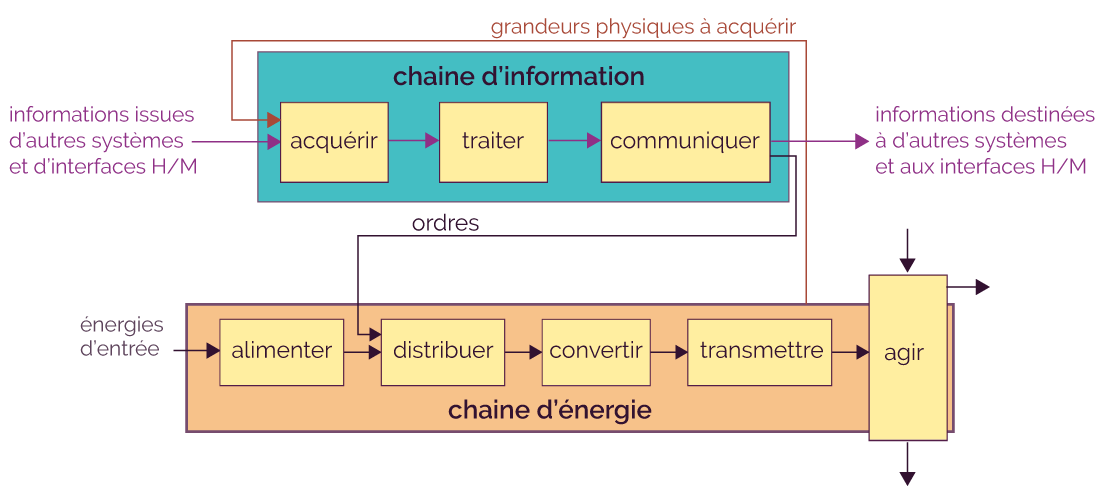
Chaines d’information et d’énergie

Cette fonction est utilisée dans les systèmes de transformation de mouvement, qui permettent d’adapter le mouvement à l’utilisation visée.

Les objectifs visés peuvent être :

changer la direction du mouvement ;
changer l’intensité de l’effort disponible (force ou couple) ;
changer la vitesse ;
rendre le système irréversible.

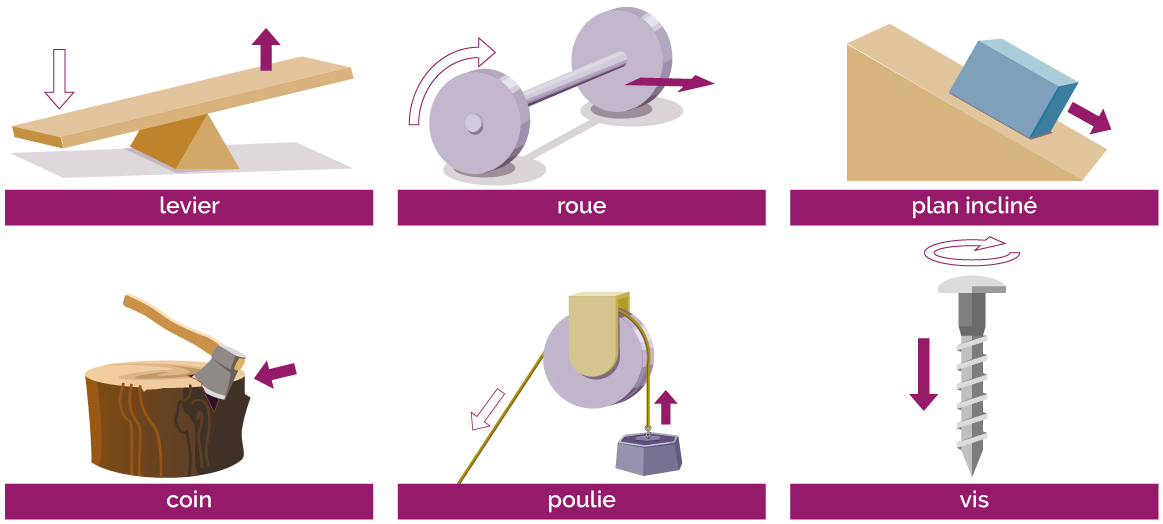Exemples de systèmes élémentaires de transformation du mouvement

L’avantage mécanique (AM) est le coefficient par lequel un mécanisme multiplie la force ou le couple de forces appliquées.

Il y a une contrepartie à cette augmentation de l’effort : la distance à parcourir augmente.

Rappels

On appelle force l’action mécanique exercée par un objet sur un autre objet. Cette action mécanique peut empêcher ou provoquer le mouvement d’un objet et aussi le modifier. Elle s’exprime en newton (N).
En mécanique, un couple correspond à un ensemble de deux forces qui ont pour action de mettre en rotation un solide. Le couple correspond donc à l’effort de rotation qui est appliqué à un axe. Il s’exprime en newton mètre (N·m).

2. Les principaux systèmes de transformation de mouvement et leur application fonctionnelle

Les systèmes présentés ci-dessous permettent de transformer le mouvement. Les formules associées sont données et l’on indique si le système est réversible ou non.

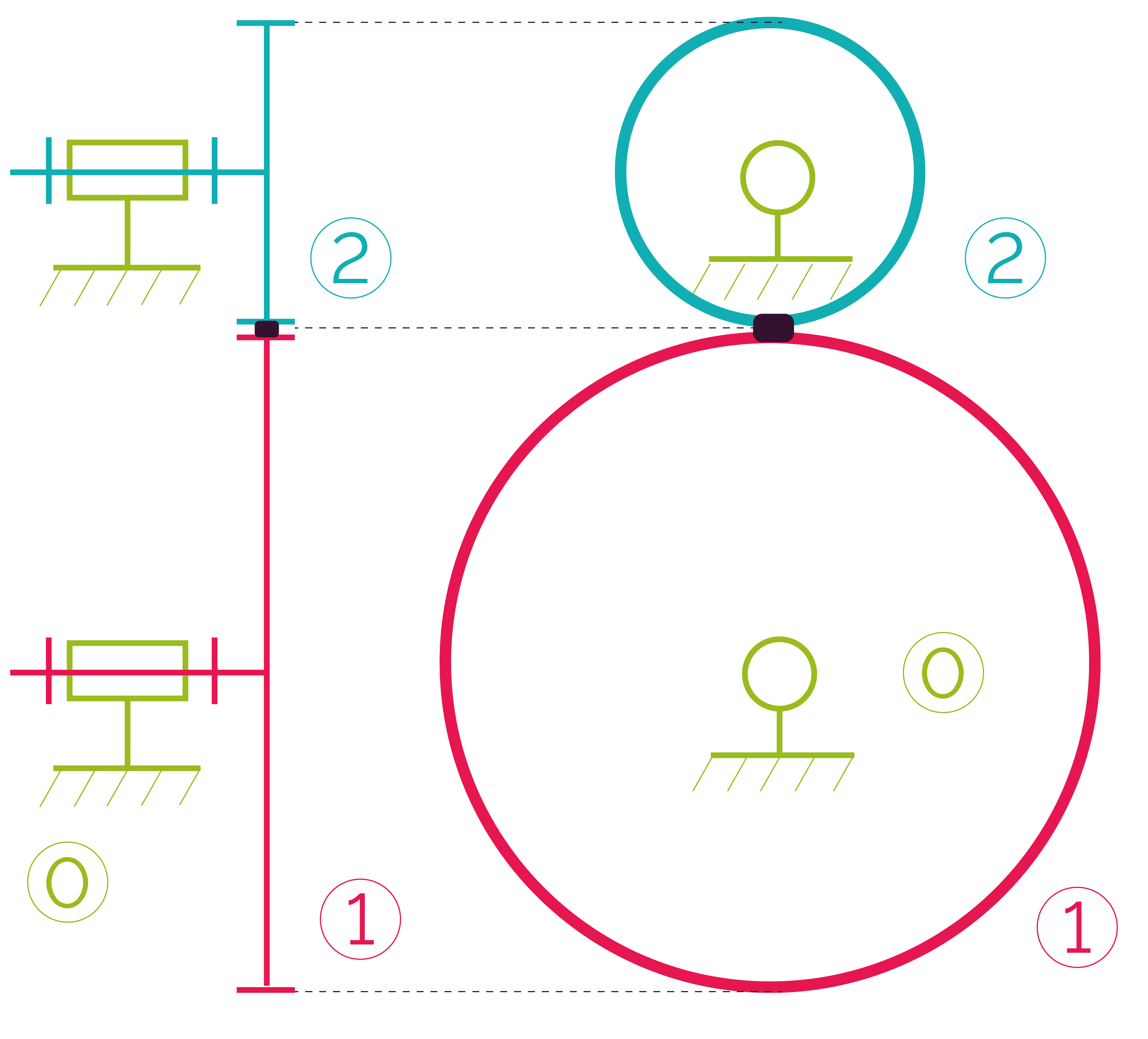
Le système est dit réversible si le mouvement de sortie peut entrainer le mouvement d’entrée.

a. La transformation du mouvement de rotation en rotation

Les systèmes présentés ci-dessous permettent de transformer un mouvement de rotation en rotation.

Engrenage

Un engrenage est un système mécanique composé de deux roues dentées ou plus, qui permet de transmettre une puissance mécanique de rotation.

Si les diamètres des roues sont différents, alors cela modifie le couple et la vitesse de rotation en sortie par rapport à leur valeur en entrée.

On peut alors calculer le rapport de transmission, qui correspond au ratio existant entre les vitesses de rotation de plusieurs roues dentées.

Si le rapport est inférieur à 1, on parle de rapport de réduction.

Pour calculer le rapport de transmission d’un engrenage, on a besoin de connaitre le nombre de dents (noté Z) de chaque roue dentée.

Le rapport de transmission se note généralement R.

avec :

R le rapport de transmission, sans unité
Z le nombre de dents des roues

Remarque
On nomme « pignon » la petite roue dentées et « roue» la plus grande roue dentée.

Ce système est réversible.

Train d’engrenages

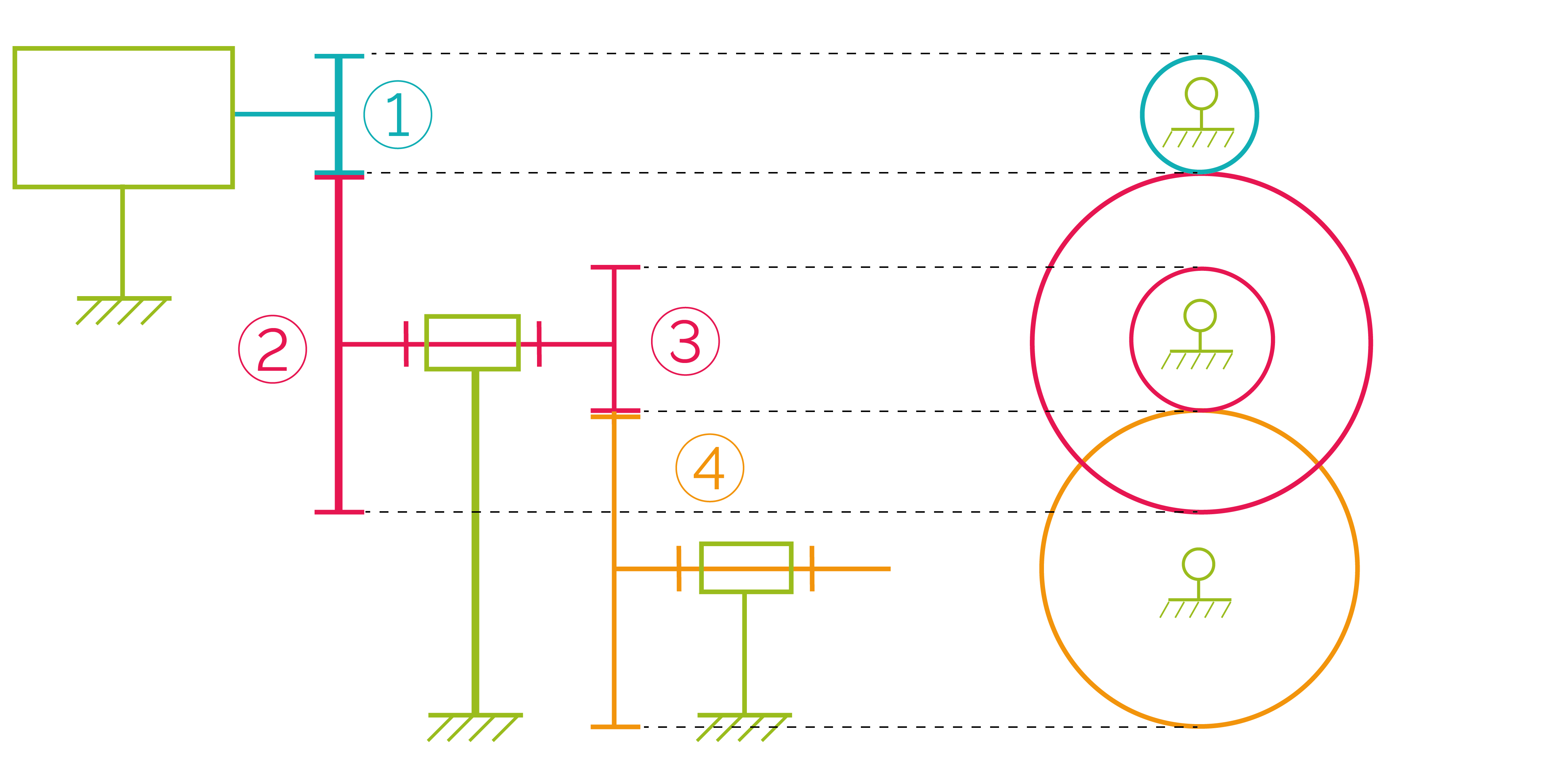
On parle de train d’engrenages lorsqu’il y a plus de deux roues dentées.

Ici :

Ce système est réversible.

Roue-vis sans fin

Un système roue-vis sans fin est composé d’une vis sans fin et d’une roue hélicoïdale.
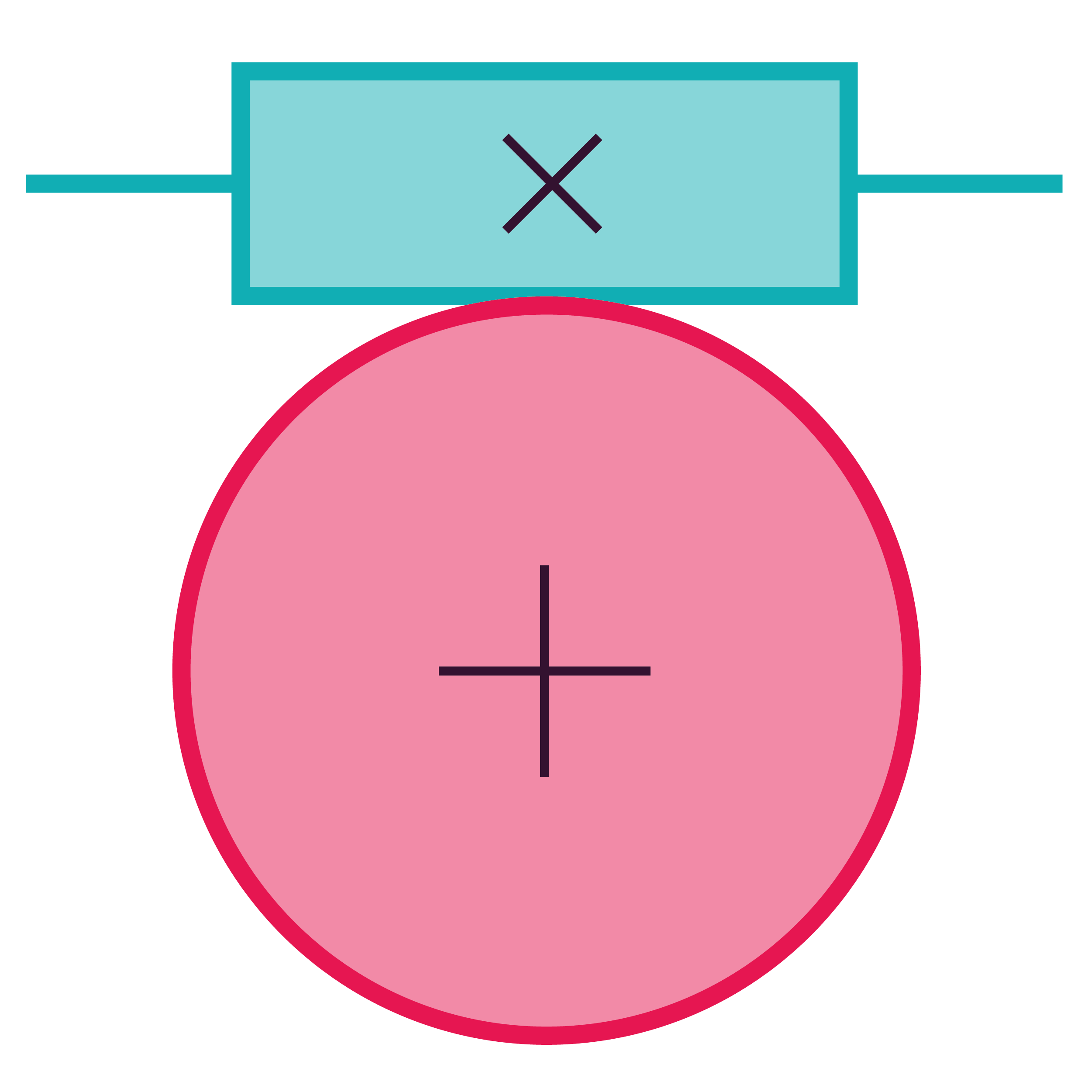
Ce système permet d’adapter la vitesse de rotation et/ou le couple, de même qu’il permet de changer l’axe de rotation.

Avec un système roue-vis sans fin, on peut obtenir un très grand rapport de réduction avec un encombrement réduit.

Le système est, en général, irréversible car la roue ne peut pas entrainer la vis.

avec :

R le rapport de transmission, sans unité
ω la vitesse de rotation, en radian par seconde (rad/s)
Z₁ le nombre de filets de la vis sans fin
Z₂ le nombre de dents de la roue

Poulies-courroie

Les courroies à section circulaire, trapézoïdale ou rectangulaire permettent de transmettre un mouvement de rotation avec glissement. Cela peut être utilisé comme une sécurité sur certains systèmes.

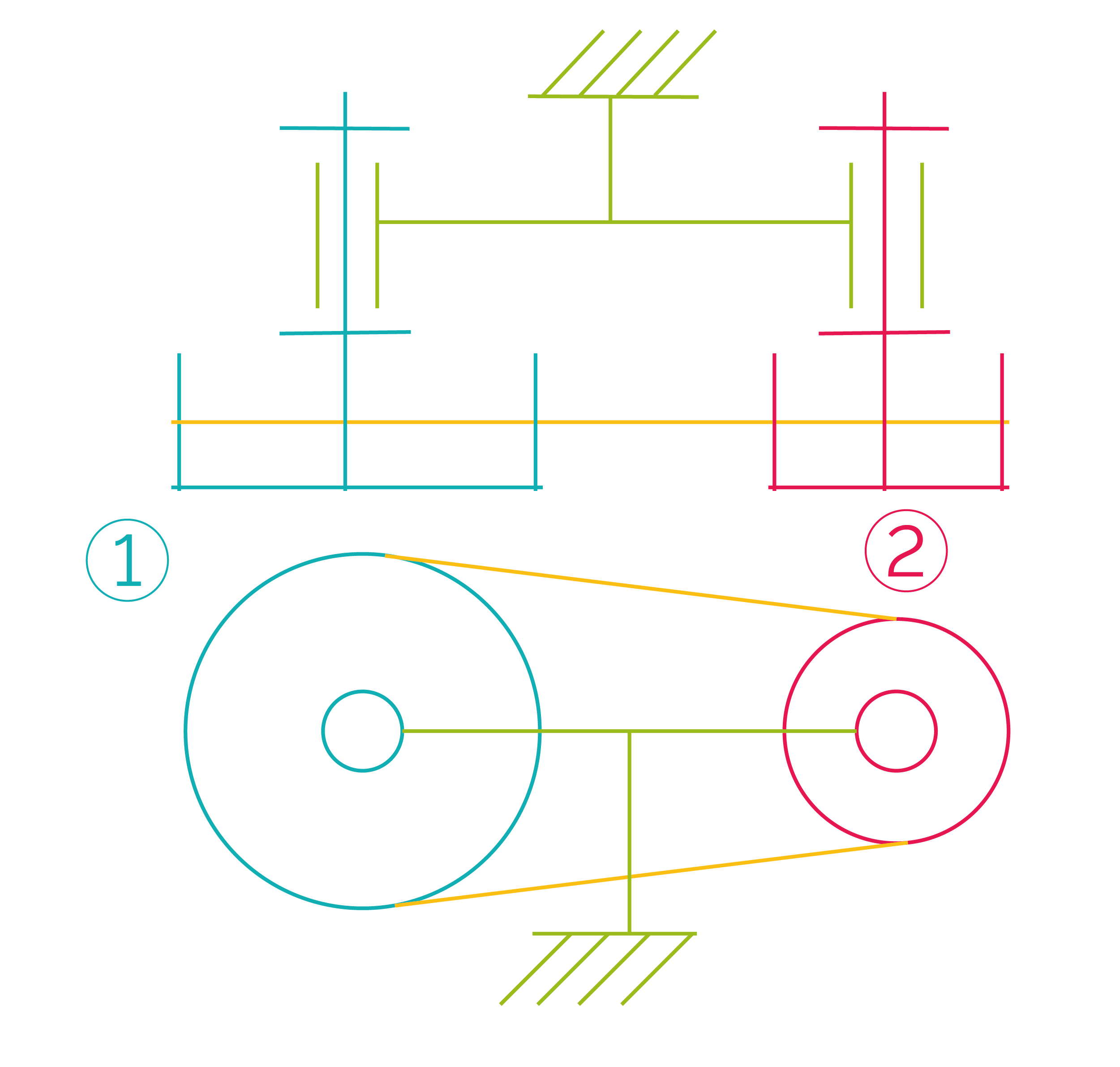
Les poulies crantées et la courroie associée assurent une transformation de mouvement sans glissement. Comme les engrenages, cette transformation de mouvement est par obstacle, donc avec conservation des positions relatives des poulies à tout instant.

Si les diamètres des poulies sont différents, la vitesse et le couple de forces en sortie seront alors différents de ceux en entrée.

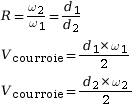
avec :

R le rapport de transmission, sans unité
d₁ le diamètre de la poulie motrice, en mètre (m)
d₂ le diamètre de la poulie réceptrice, en mètre (m)
ω₁ la vitesse angulaire de la poulie motrice, en radian par seconde (rad/s)
ω₂ la vitesse angulaire de la poulie réceptrice, en radian par seconde (rad/s)
V la vitesse de translation de la courroie, en mètre par seconde (m/s)

Ce système est réversible.

Croix de Malte

La croix de Malte est un dispositif mécanique qui permet de transformer un mouvement de rotation continue en une rotation saccadée.

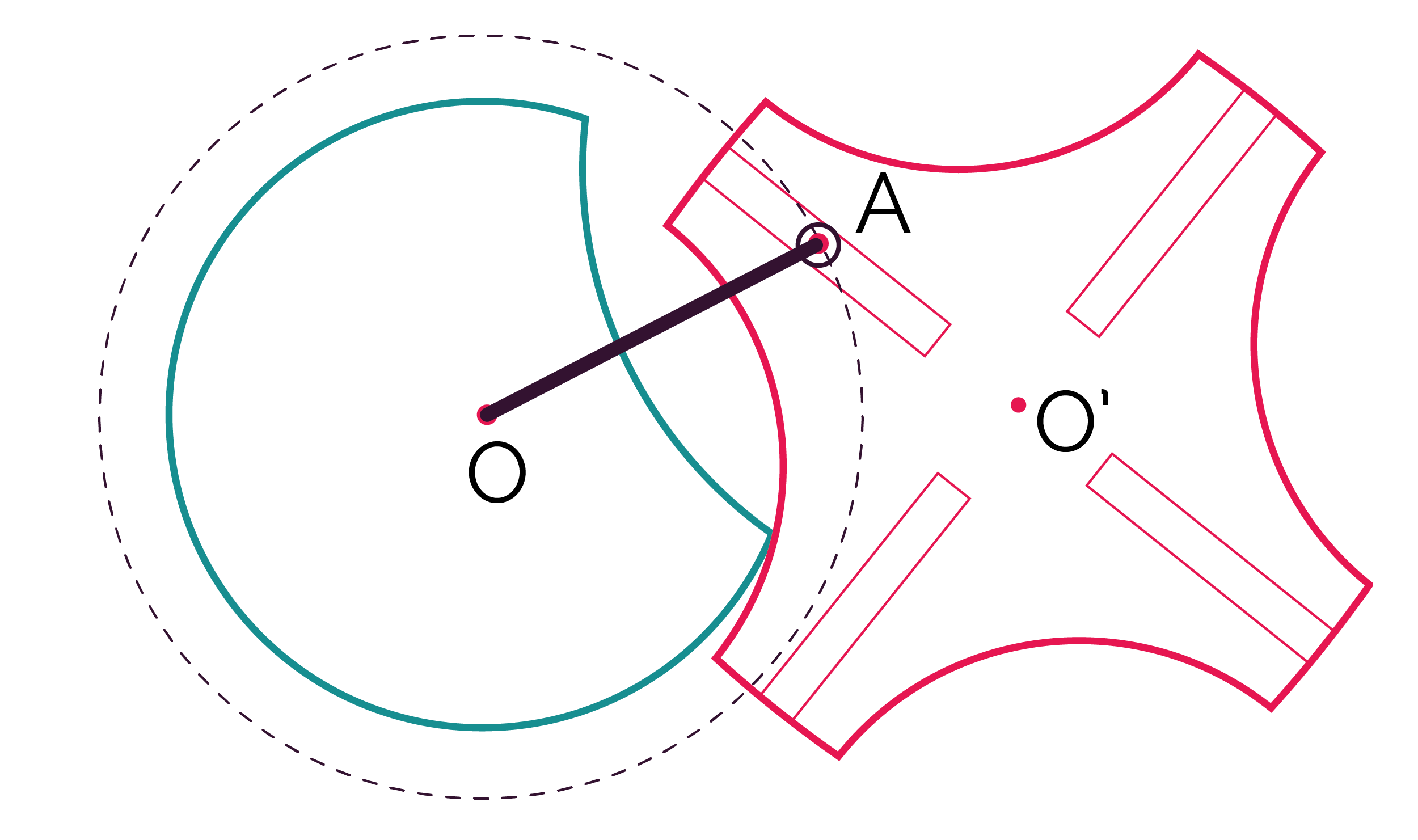
Ce système est composé d’une pièce en rotation continue munie d’un ergot, et d’une croix de Malte, laquelle est une pièce en rotation intermittente qui est munie de rainures. L’ergot de la pièce en mouvement continu permet d’entrainer la pièce en mouvement intermittent en s’intégrant dans la rainure.

Ce système est irréversible car seule la pièce en mouvement continu peut l’actionner.

b. La transformation du mouvement de rotation en translation ou inversement

Les systèmes présentés ci-dessous permettent de transformer un mouvement de rotation en translation ou inversement.

Pignon-crémaillère

Un système pignon-crémaillère est composé d’une roue dentée (nommée « pignon ») et d’une tige dentée (nommée « crémaillère »).
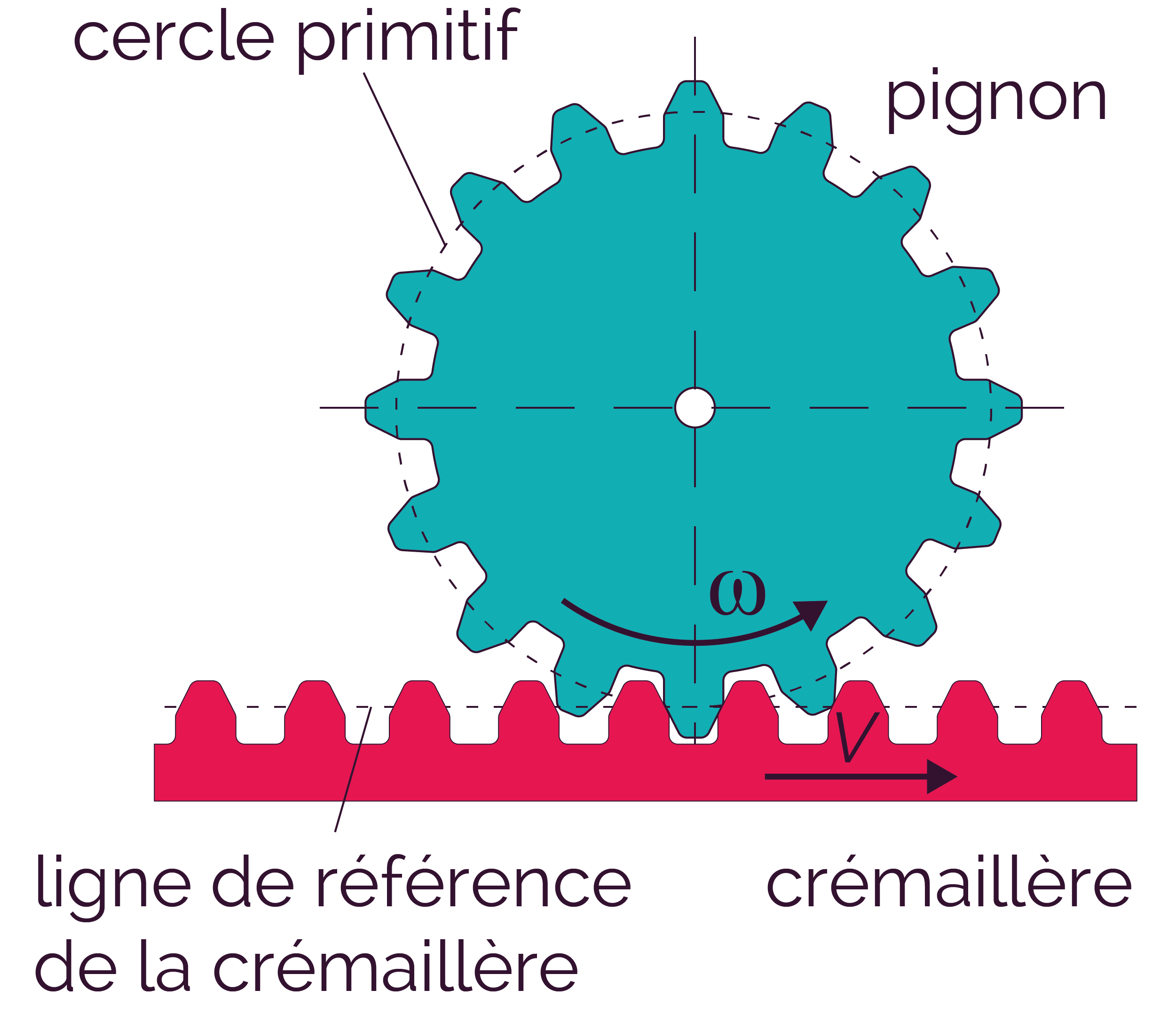
Ce système permet de transformer un mouvement de rotation en mouvement de translation, et vice versa.

Lors du mouvement, le cercle primitif de la roue se déplace sans glissement sur la ligne de référence de la crémaillère. On peut donc calculer la distance parcourue par la roue sur la crémaillère et sa vitesse de déplacement.

avec :

d la distance parcourue par la roue sur la crémaillère, en mètre (m)
r le rayon primitif du pignon, en mètre (m)
θ l’angle de rotation du pignon, en radian (rad)

avec :

V la vitesse de déplacement de la roue sur la crémaillère, en mètre par seconde (m/s)
r le rayon primitif du pignon, en mètre (m)
ω la vitesse de rotation, en radian par seconde (rad/s)

Ce système est réversible, car le mouvement peut se faire du pignon à la crémaillère ou inversement.

Vis-écrou

Le système vis-écrou permet de transformer un mouvement de rotation en un mouvement de translation.

avec :

d la distance en millimètre (mm)
p le pas de vis, en millimètre par tour (mm/tour)
θ l’angle, en tour

Remarque
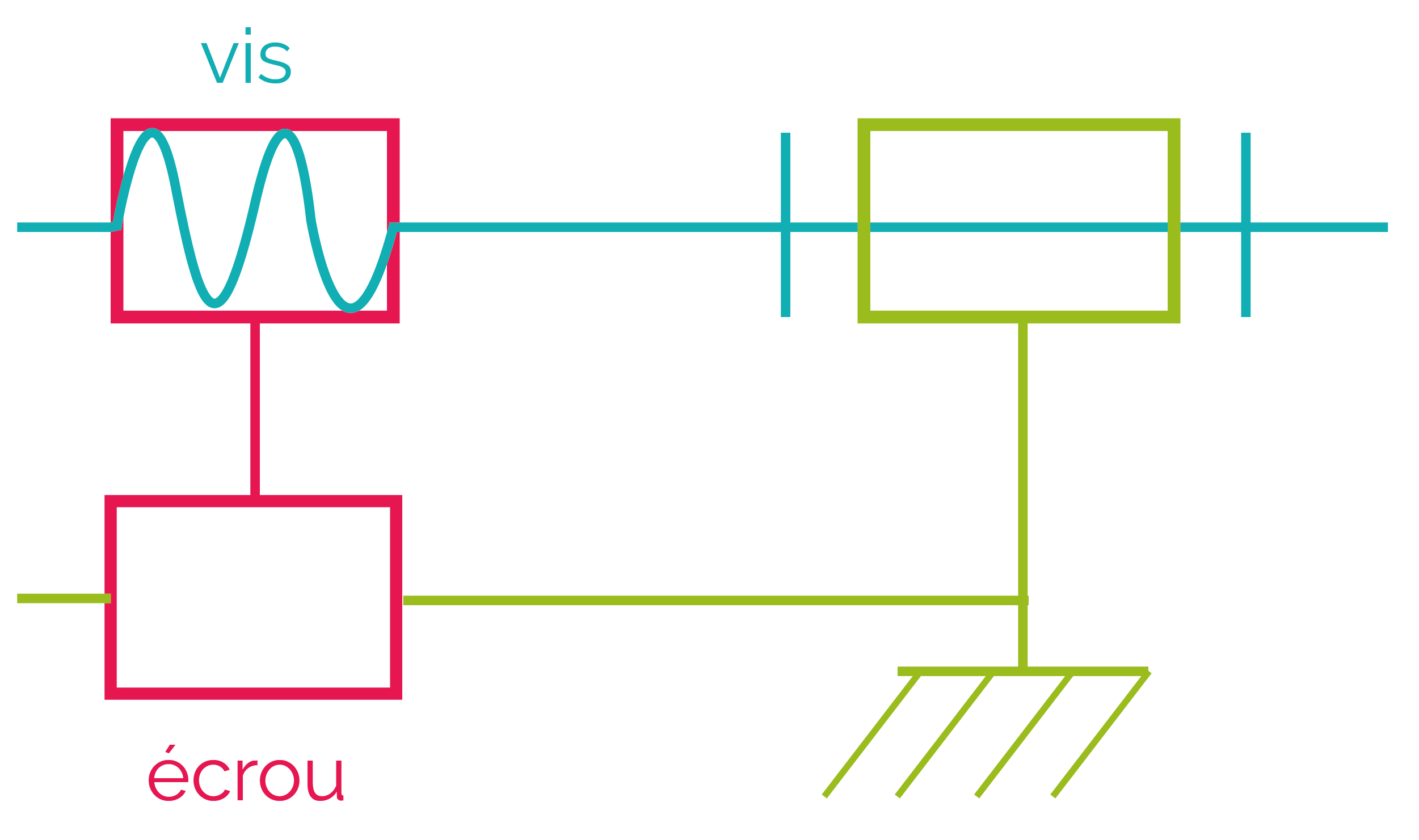
Lors d’un tour complet, une vis parcourt une distance relative par rapport à son écrou qui correspond au pas de vis.

Ce système est, en général, irréversible, car le mouvement ne peut être amorcé que par une rotation de la vis et non pas par un mouvement de l'écrou.

Système de came et tige-poussoir

Le système de came et tige-poussoir est composé d’une pièce mécanique non circulaire qui a un mouvement de rotation et met en mouvement une tige.

Ce système transforme un mouvement de rotation en un mouvement de translation alternatif (va-et-vient).

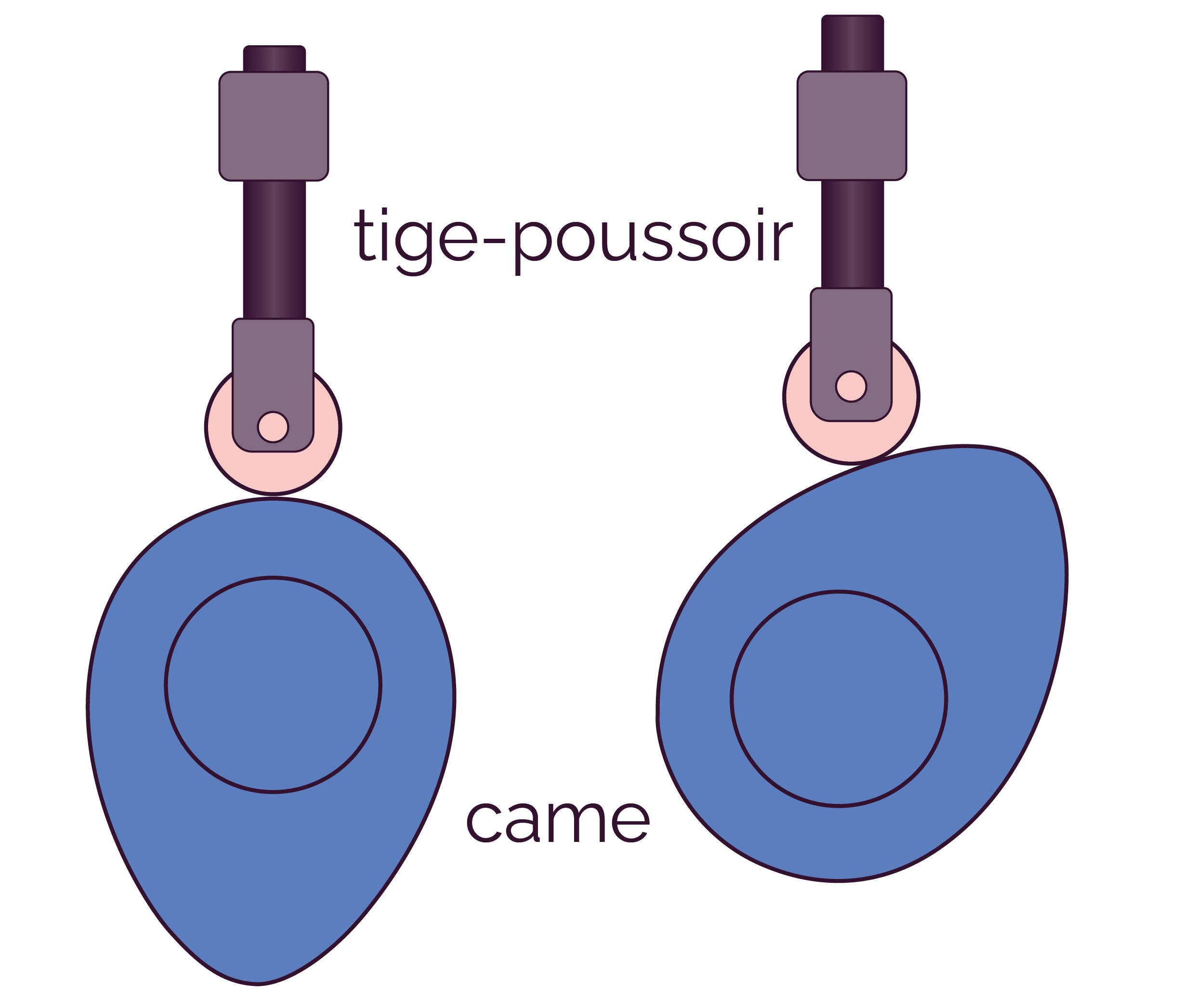
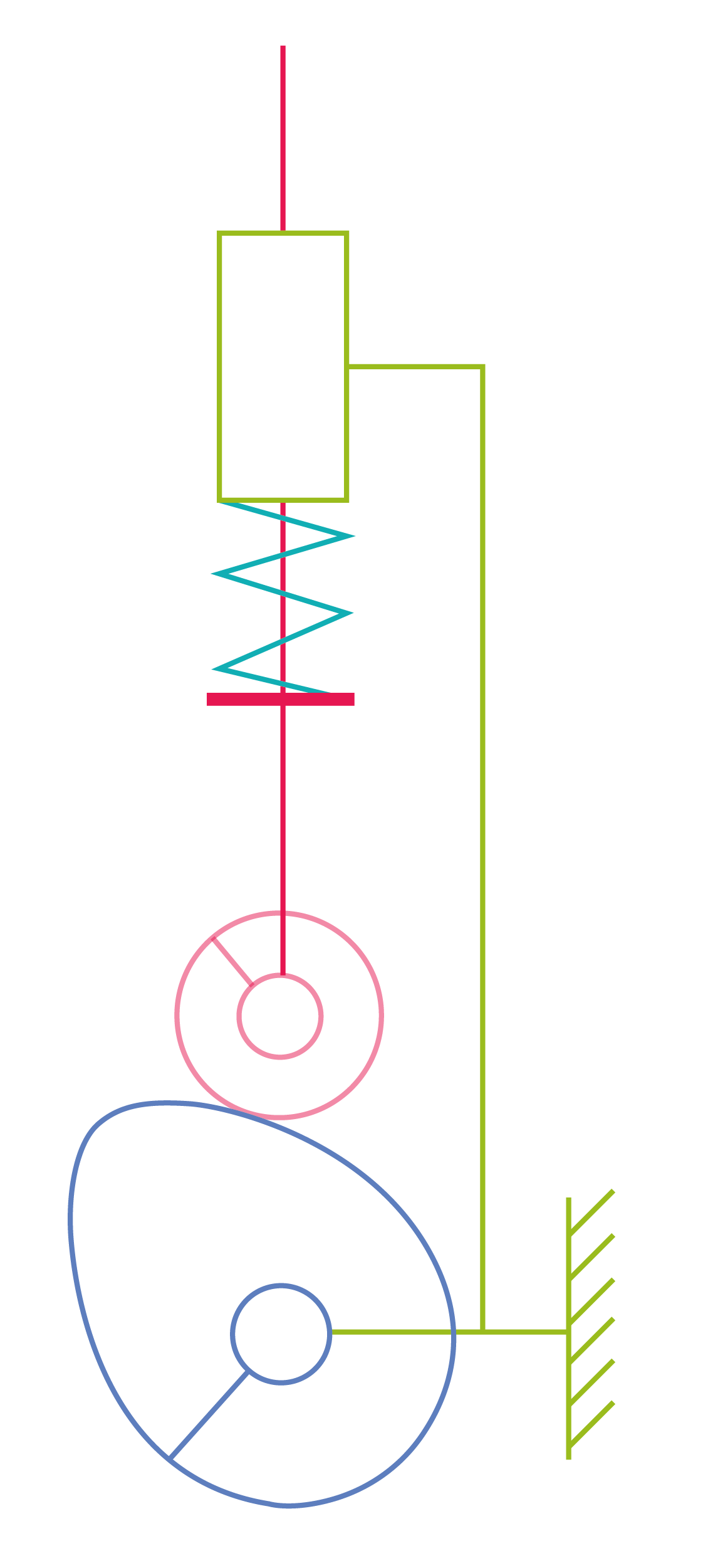
Ce système est irréversible car seule la came peut l’actionner.

Système bielle-manivelle

Le système bielle-manivelle permet de transformer, par l’intermédiaire d’une bielle (pièce dotée de deux articulations), un mouvement de translation alternatif en mouvement de rotation continu, et réciproquement.

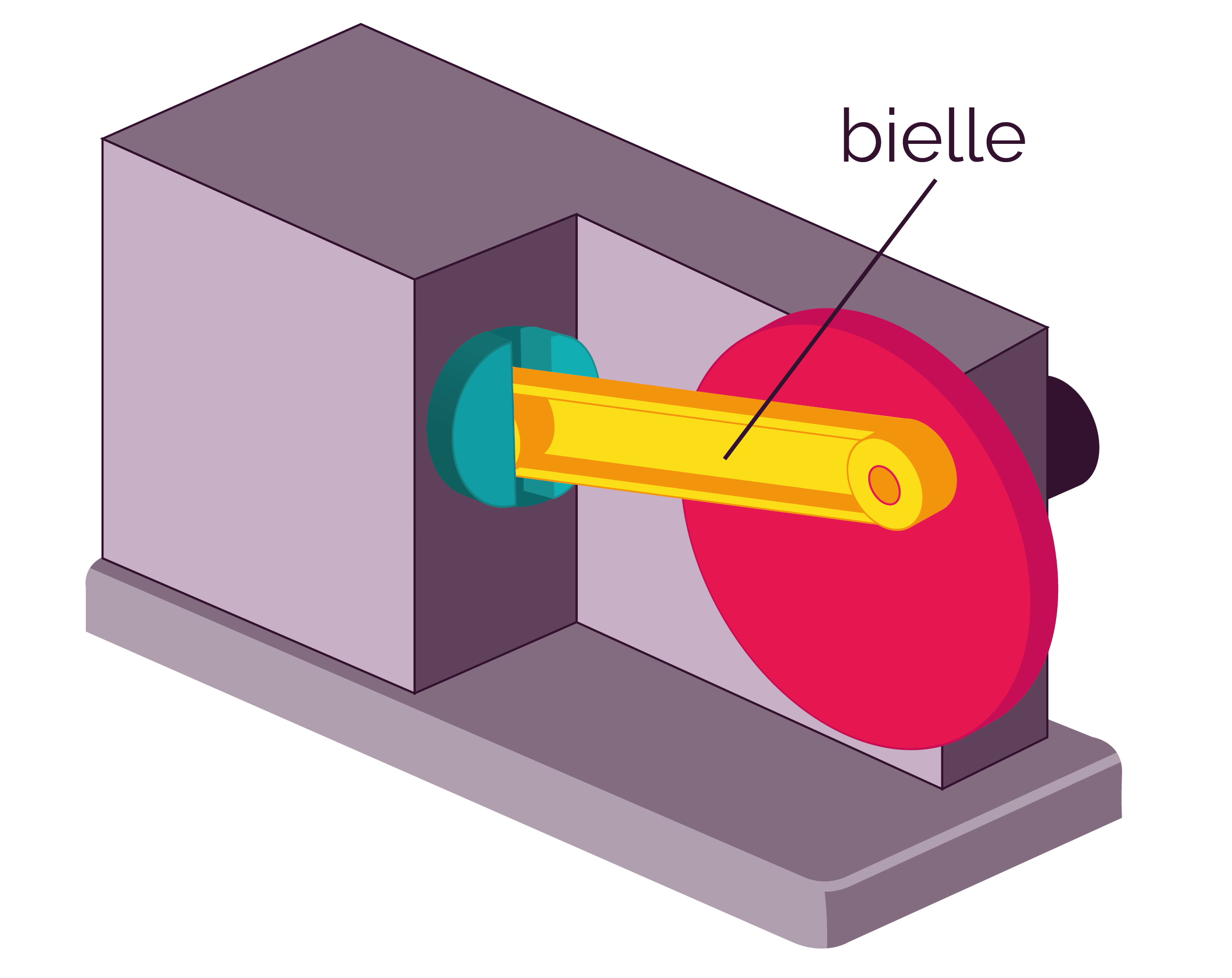
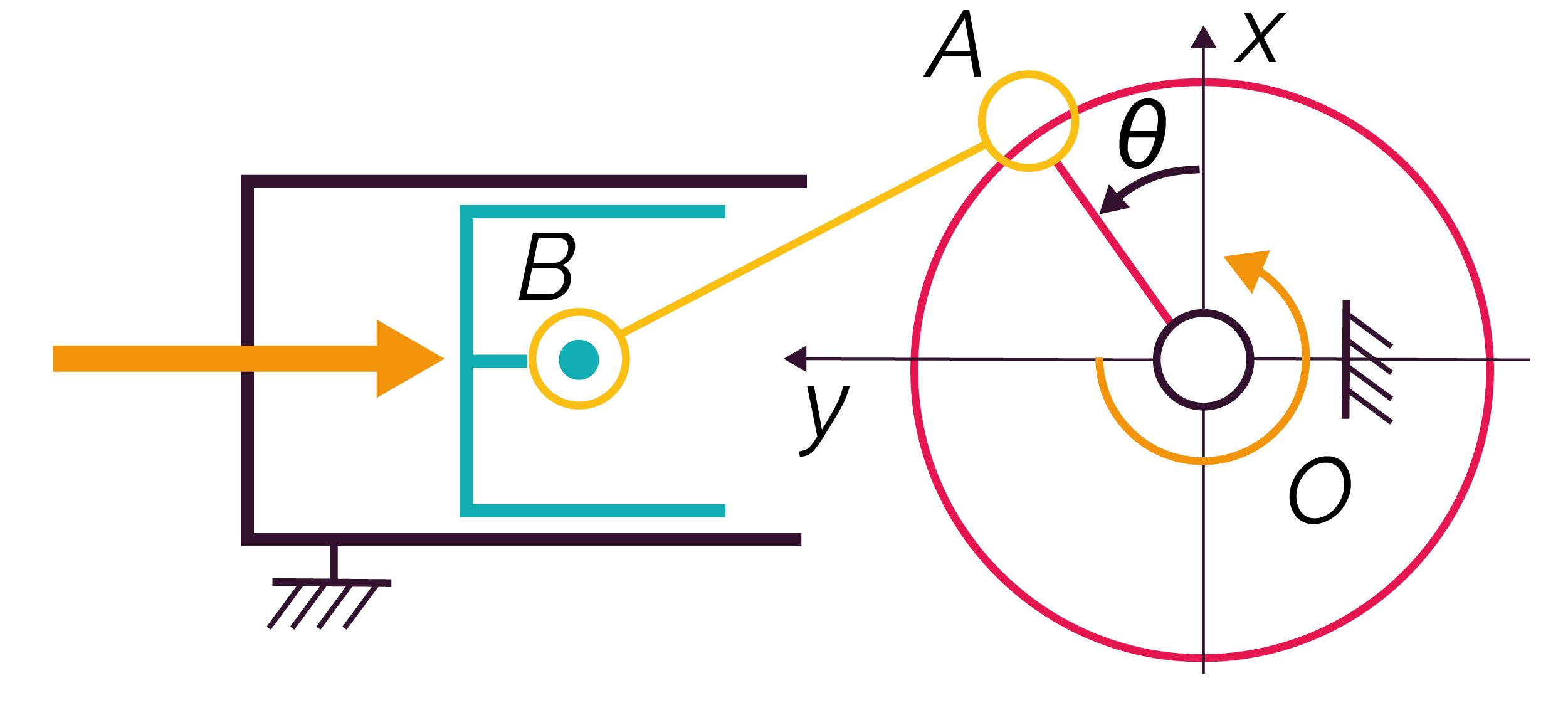
Ce système est réversible car l’organe moteur peut être la bielle comme la manivelle.