La notion de limite de suite
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Étudier le comportement de un lorsque n prend des valeurs de plus en plus grandes.
Lorsque n tend vers l'infini, une suite peut :
- soit converger vers un réel (fini). Dans ce cas, ses valeurs « se stabilisent autour de la valeur limite » ;
- soit tendre vers +∞ ou –∞, soit n'admettre aucune limite (même infinie), dans ce cas, on dit qu'elle diverge.
- Notion de suite, de terme général d'une suite
- Représentation graphique des termes d'une suite
- Fonctions de référence
- Manipulation d'inéquations
On considère la suite ![]() définie
par
définie
par ![]() .
.
Observons le comportement de un lorsque
n prend
de très grandes valeurs positives.
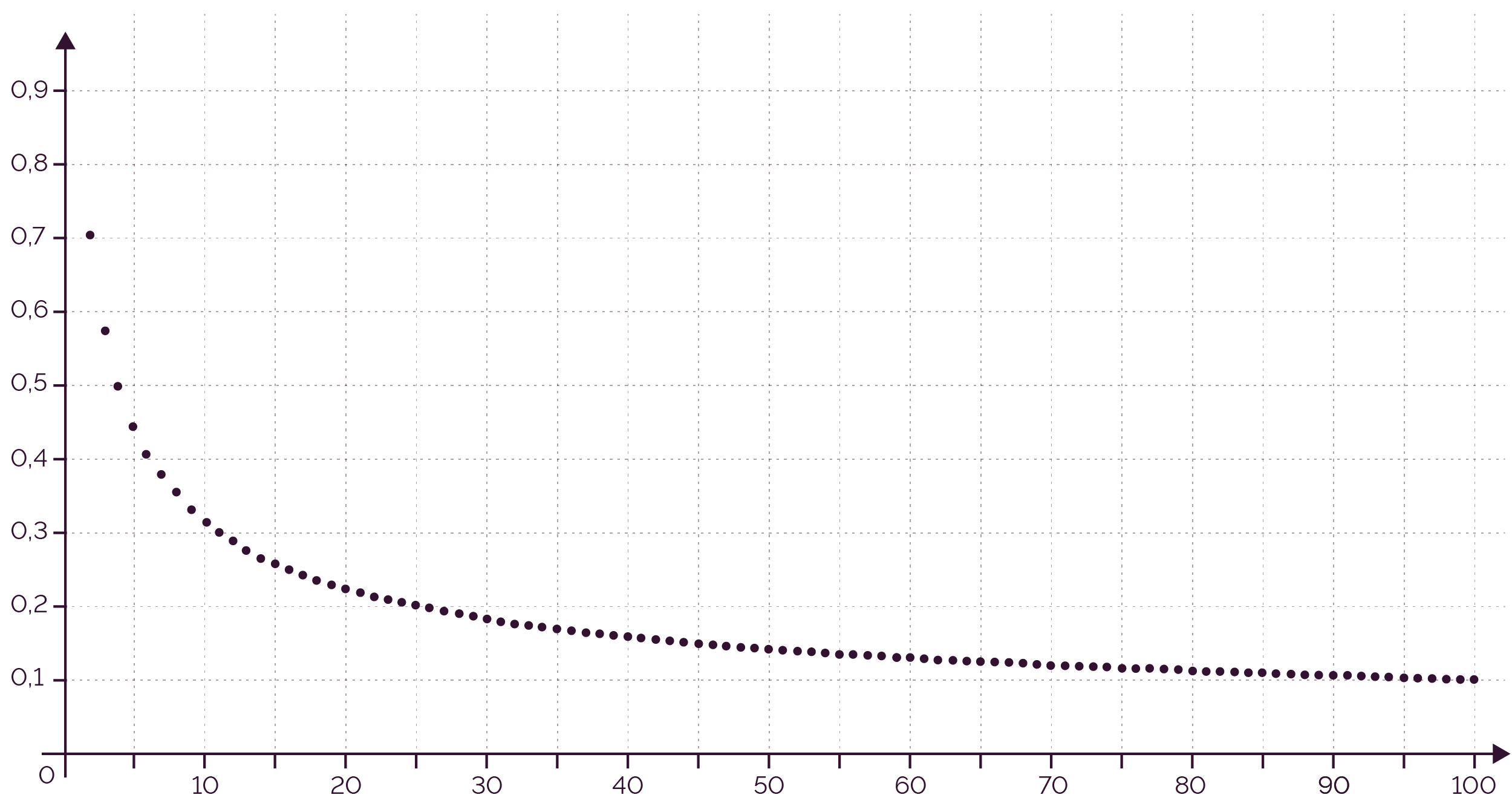
| n | 1 | 10 | 50 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 |
| un | 1 | 0,32 | 0,14 | 0,1 | 0,03 | 0,0100000 | 0,0031623 | 0,0010000 |
Il semblerait que les termes de la suite s'accumulent
près de 0 lorsque n tend vers
+∞.
Comment expliquer cette accumulation ?
Donnons-nous un intervalle contenant 0, par
exemple ![]() .
.
Existe-t-il un rang à partir duquel tous les
un rentrent
dans cet intervalle ?
Pour cela, résolvons la double
inéquation ![]() .
.
Tout d'abord,
l'inégalité ![]() est toujours
vérifiée puisque
est toujours
vérifiée puisque ![]() est toujours positif donc
à fortiori plus grand qu'un nombre
négatif.
est toujours positif donc
à fortiori plus grand qu'un nombre
négatif.
Déterminons n tel
que ![]() soit
soit ![]() .
.
La fonction inverse est décroissante
sur ![]() donc cela revient à
dire que
donc cela revient à
dire que ![]() soit
soit ![]() .
.
Conclusion : à partir de ![]() ,
, ![]() .
.
On démontre de même que pour tout
intervalle ouvert I contenant 0, il
existe un rang tel que pour tout n supérieur
à ce rang, un soit
dans I.
Ainsi, les termes de la suite s'accumulent près
de 0.
On dira que la suite ![]() converge (tend)
vers 0 ou la suite
converge (tend)
vers 0 ou la suite ![]() a pour limite 0
lorsque n tend vers
+∞.
a pour limite 0
lorsque n tend vers
+∞.
On pourra écrire : ![]() .
.
- Les suites de terme
général
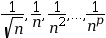 avec p entier
supérieur ou égal à 1
tendent vers 0 lorsque n tend vers
+∞.
avec p entier
supérieur ou égal à 1
tendent vers 0 lorsque n tend vers
+∞.
- Les suites de terme
général
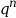 où
où 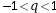 tendent vers 0
lorsque n tend vers
+∞.
tendent vers 0
lorsque n tend vers
+∞.
On considère la suite ![]() définie
par
définie
par ![]() .
.
Observons de même le comportement de
un lorsque
n prend
de très grandes valeurs positives.
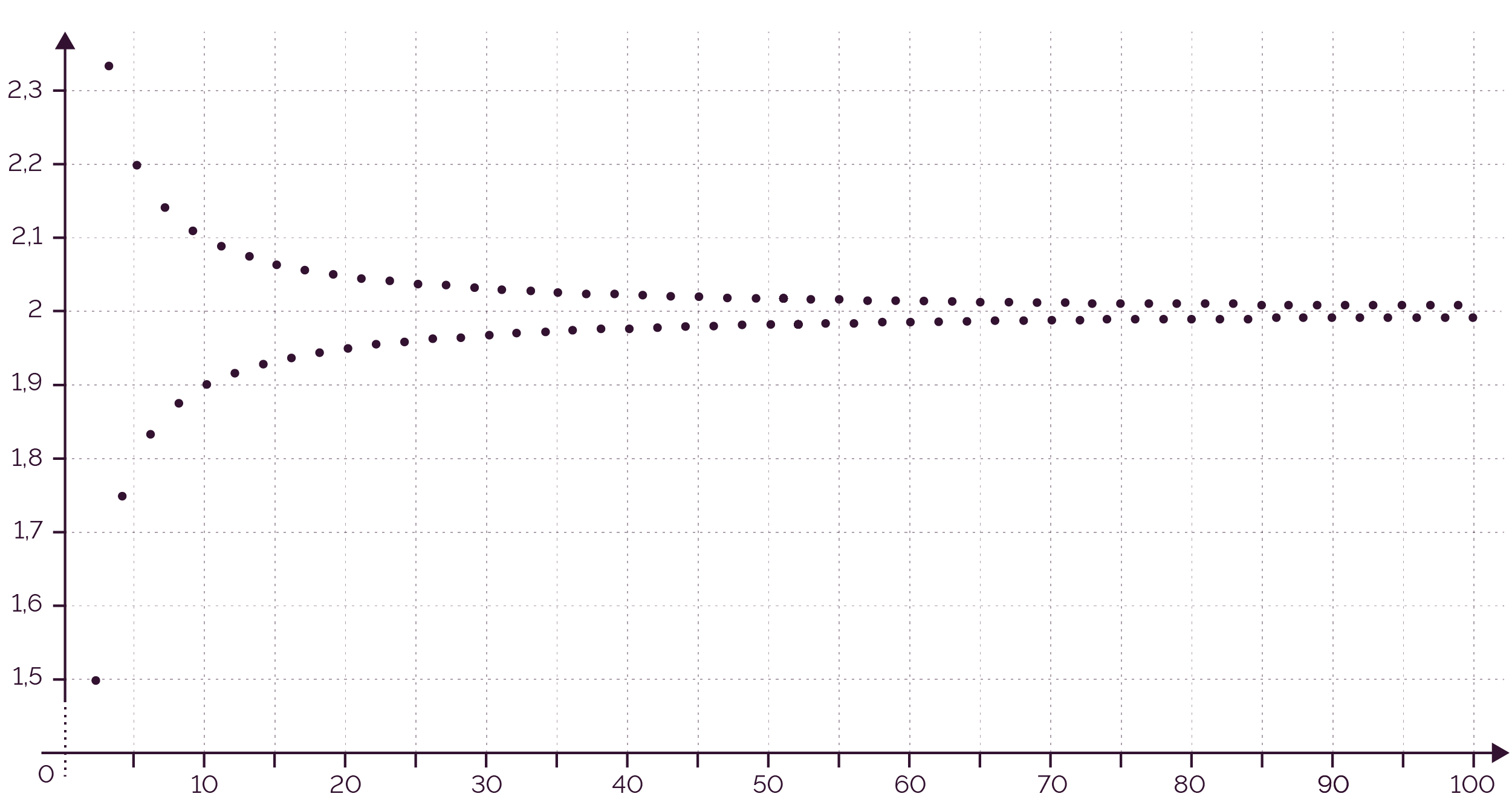
Il semblerait que les termes de la suite
s’accumulent autour de 2 lorsque
n tend
vers +∞, mais
alternativement au dessus, en dessous de 2.
La suite ![]() est également une
suite convergente et elle a pour limite 2.
est également une
suite convergente et elle a pour limite 2.
On pourra écrire : ![]() .
.
Considérons la suite ![]() définie par
définie par
![]() .
.
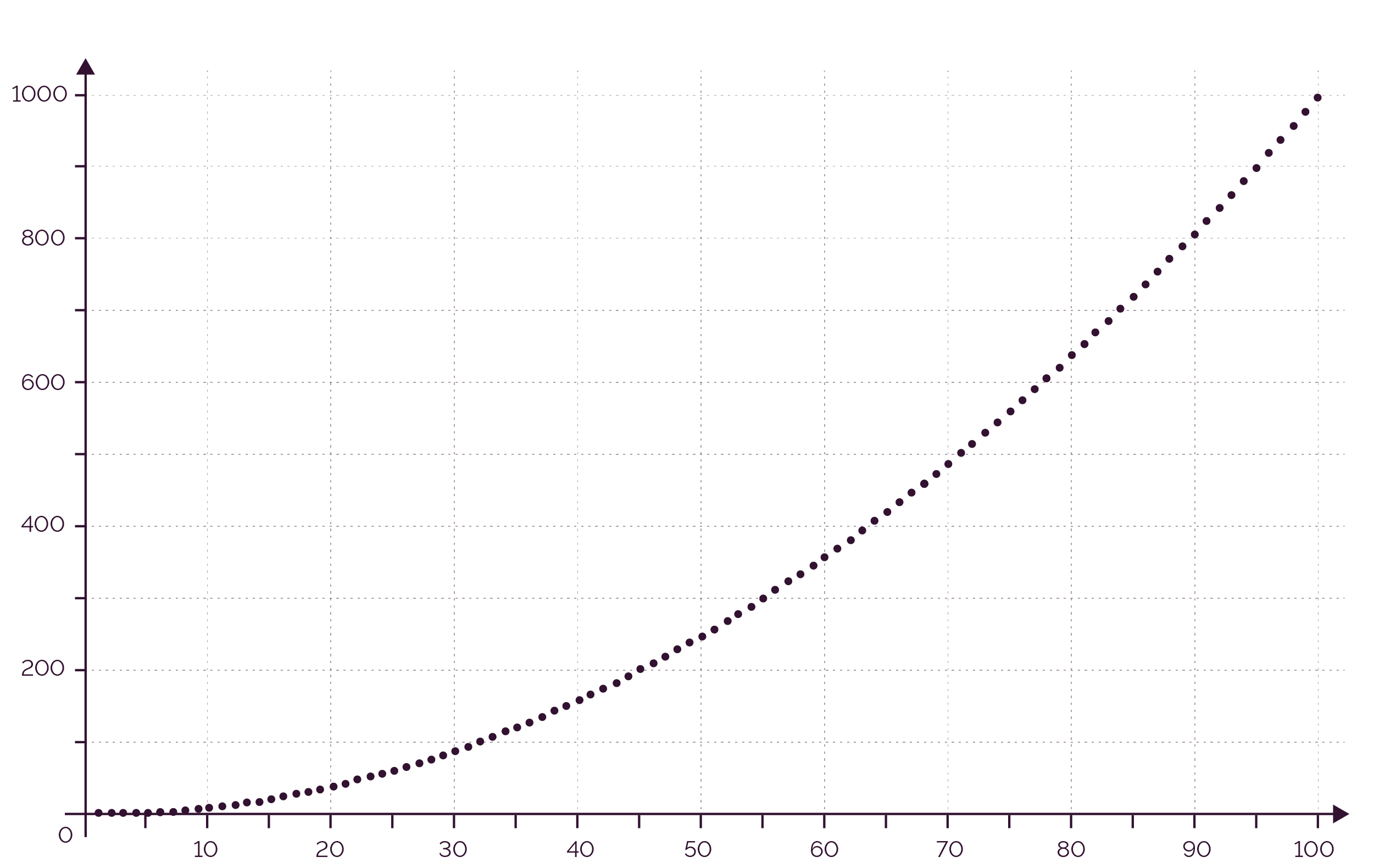
Observons le comportement de un lorsque n prend de grandes valeurs.
|
|
0 | 1 | 10 | 50 | 100 | 1000 | 10 000 | 100 000 |
|
|
–1 | –0,9 | 9 | 249 | 999 | 99 999 | 9 999 999 | 999 999 999 |
Il semblerait que les termes de la
suite ![]() deviennent de plus en plus
grand et tendent vers +∞ lorsque n tend vers
+∞.
deviennent de plus en plus
grand et tendent vers +∞ lorsque n tend vers
+∞.
Comment expliquer cette divergence vers +∞ ?
Il s'agit de prouver que l'on ne peut arrêter la progression des termes un et qu'ils finissent par dépasser n'importe quel nombre, aussi grand soit-il.
Prenons par exemple A = 106.
Existe-t-il un rang n0 tel
que pour ![]() , on ait
, on ait ![]() ?
?
![]()
![]()
![]()
![]()
Ainsi, à partir de u101, les
termes un sont
supérieurs à 106.
On démontre de même que ceci est vrai pour
tout nombre réel A choisi aussi grand que
l’on veut.
On dit alors que la suite ![]() tend vers +∞ lorsque
n tend
vers +∞.
tend vers +∞ lorsque
n tend
vers +∞.
On pourra écrire : ![]() .
.
- Les suites de terme
général
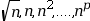 avec p entier
supérieur ou égal à 1
tendent vers +∞ lorsque
n tend vers
+∞.
avec p entier
supérieur ou égal à 1
tendent vers +∞ lorsque
n tend vers
+∞.
- Les suites de terme
général
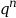 avec
avec 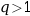 tendent vers
+∞ lorsque
n tend vers
+∞.
tendent vers
+∞ lorsque
n tend vers
+∞.
Lorsque les termes d'une suite
Considérons par exemple la
suite ![]() définie
par
définie
par ![]() .
.
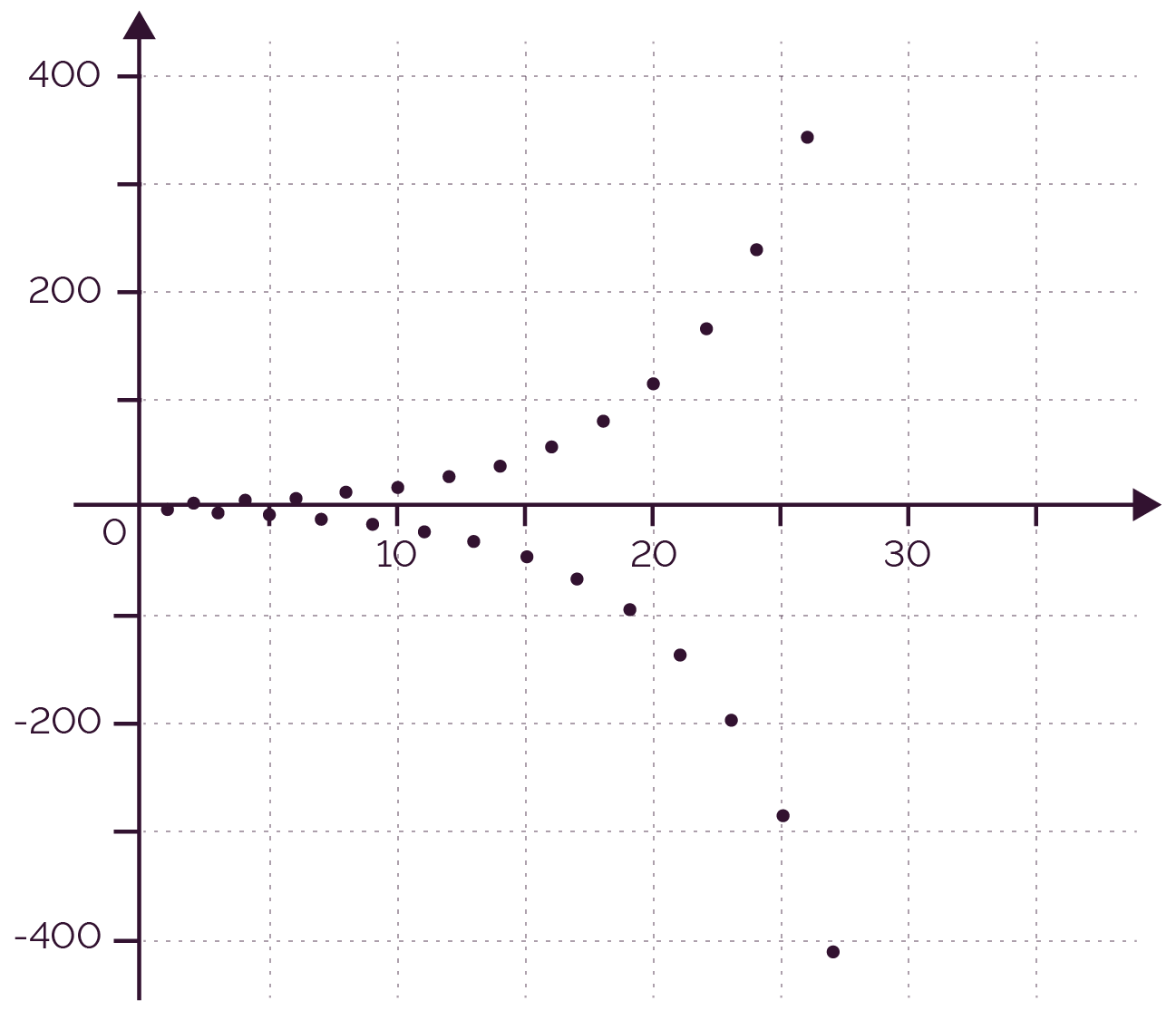
Les termes de la suite sont alternativement positifs
puis négatifs mais de plus en plus grands en
valeur absolue.
La suite est divergente, sans admettre de limite. On ne
peut pas « canaliser » la
direction des termes un.
C'est le cas notamment de toute suite
géométrique de raison strictement
inférieure à –1.
On ne pourra pas utiliser la notation ![]() lorsque aucune limite
n'existe pour la suite étudiée.
lorsque aucune limite
n'existe pour la suite étudiée.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








