Lycée > Terminale > Physique Chimie > Exploiter la poussée d'Archimède

Exploiter la poussée d'Archimède

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectifs

Expliquer qualitativement l’origine de la poussée d’Archimède.
Utiliser l’expression de la poussée d’Archimède.

Points clés

Un fluide exerce une force pressante sur les parois d’un objet immergé : cette force pressante est perpendiculaire à la paroi, dirigée vers l’objet et sa valeur est égale au produit de la pression du fluide par la surface.
La pression dans un fluide augmente lorsque la coordonnée verticale diminue. La relation entre ces deux grandeurs nous est donnée par la loi fondamentale de la statique des fluides : la variation de pression est proportionnelle à la variation de la coordonnée verticale.
Tout objet immergé dans un fluide subit de sa part une poussée verticale, dirigée vers le haut, dont la valeur est égale au poids du fluide déplacé. C’est la poussée d’Archimède.

Pour bien comprendre

La force pressante (1^re)
Loi fondamentale de la statique des fluides (1^re)

1. La poussée d'Archimède

La poussée d’Archimède permet d’expliquer pourquoi certains objets flottent à la surface de l’eau et pourquoi d’autres coulent.

Une analyse en termes de forces pressantes permet de comprendre l’existence de cette poussée.

a. Pression et force pressante dans un fluide (rappels)

Les gaz et les liquides sont des fluides, c’est-à-dire qu’ils ont la capacité de s’écouler.

Les liquides sont des fluides incompressibles, leur masse volumique ρ est une constante pour une température fixée.

Force pressante

Tout objet plongé dans un fluide au repos subit de la part de ce fluide des forces pressantes. Ces forces pressantes ont pour origine les innombrables chocs des particules de fluide sur la surface de l’objet.

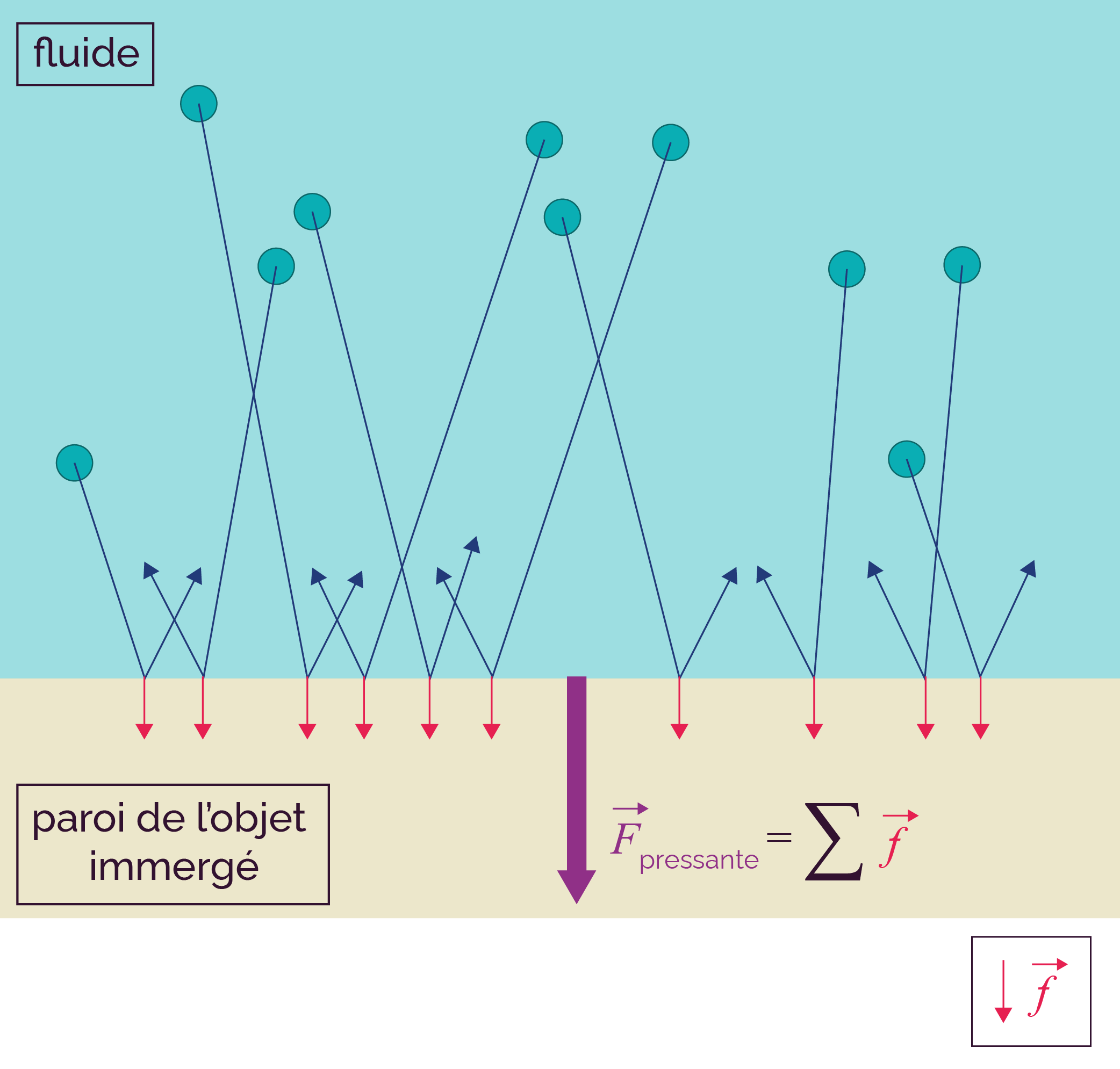
Origine de la force pressante d’un fluide

Le vecteur associé à la force pressante est perpendiculaire à la surface de l’objet et est dirigé vers l’objet.

La valeur de la force pressante dépend à la fois de la surface S de l’objet et de la pression P du fluide.

F_pressante = P × S

avec :

F_pressante la force pressante exercée par le fluide sur l’objet, en newton (N)
P la pression du fluide, en pascal (Pa)
S la surface de l’objet, en mètre carré (m²)

La loi fondamentale de la statique des fluides

La loi fondamentale de la statique des fluides relie la différence de pression entre deux positions dans un fluide incompressible et la différence entre les coordonnées verticales associées à ces positions.

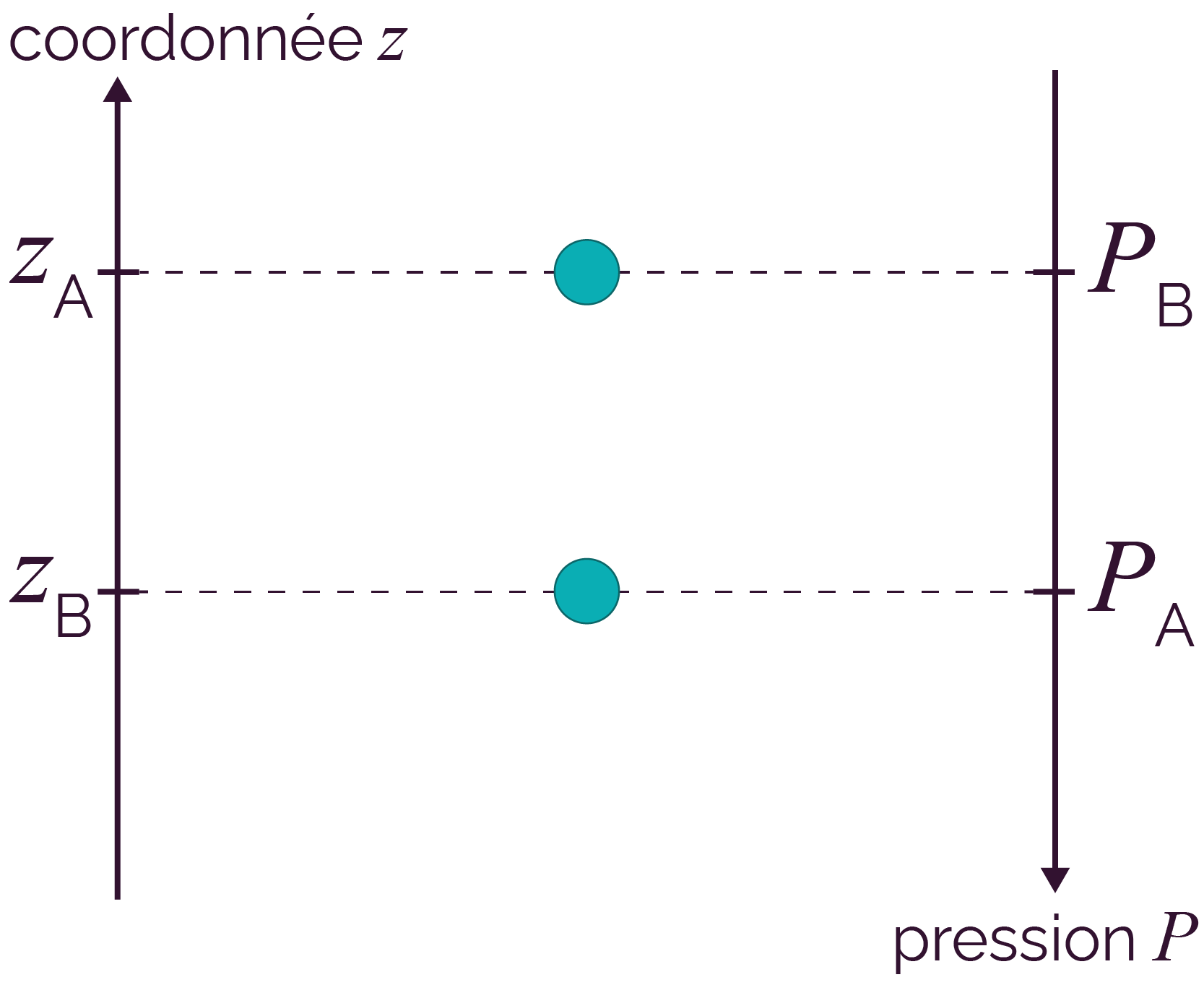
Illustration de la variation de z et de P

avec :

P_B et P_A les pressions aux points A et B, en pascal (P)
ρ la masse volumique du fluide incompressible au repos, en kilogramme par mètre cube (kg·m^–³)
Exemple : ρ_eau = 1000 kg·m^–³
g l’intensité de la pesanteur : g = 9,8 N·kg^–¹
z_B et z_A les profondeurs des points A et B, en mètre (m)

La pression augmente lorsque la coordonnée verticale diminue.

b. Origine de la poussée d'Archimède

On considère un objet cubique immergé dans un fluide et on représente les forces pressantes qui s’exercent sur les parois de celui-ci.

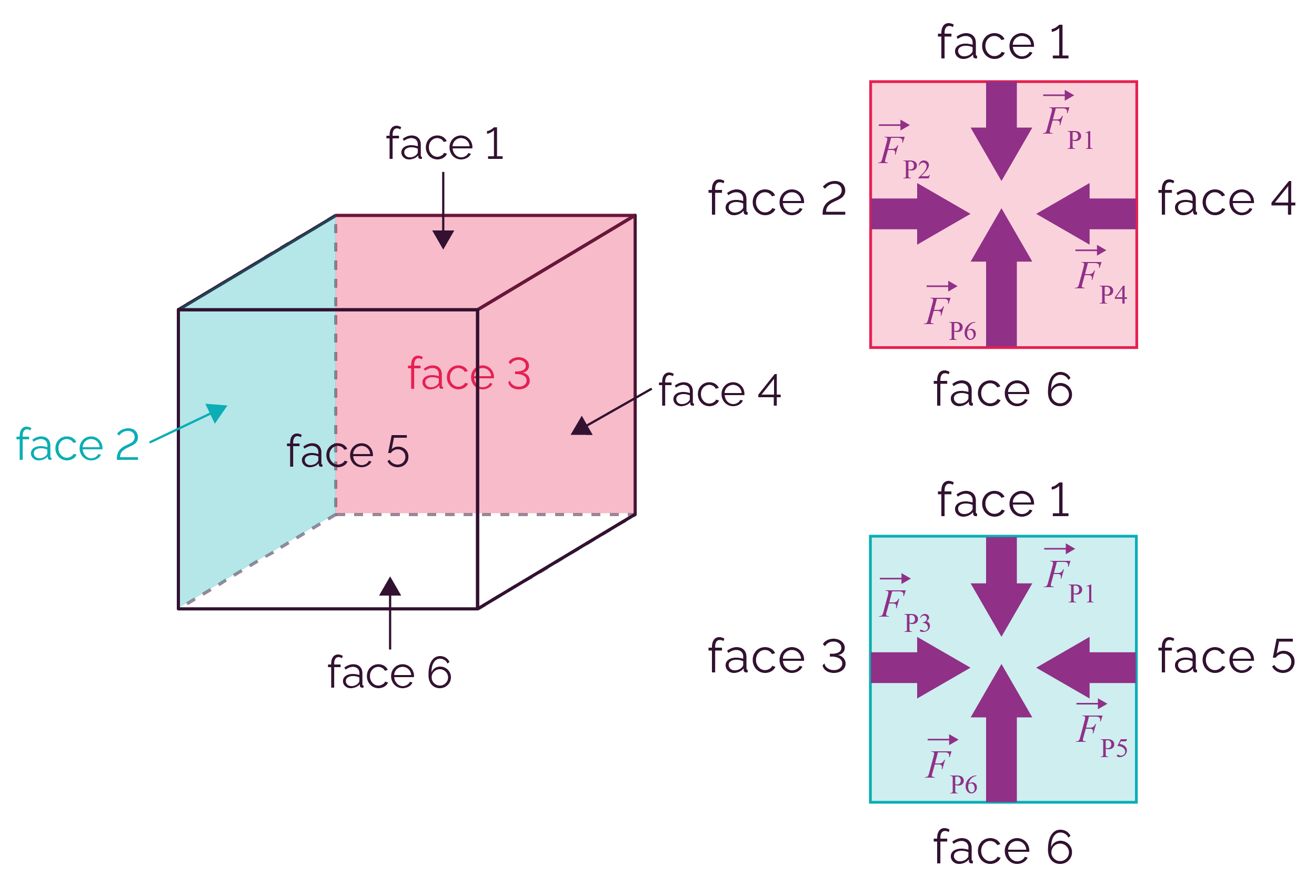
Forces pressantes exercées sur un objet cubique

Les forces pressantes sur les parois latérales

On constate que les forces pressantes sur les parois latérales se compensent deux à deux.

Ceci s’explique par le fait que les valeurs de toutes ces forces pressantes sont les mêmes : même surface S et même pression car toutes les parois ont la même coordonnée verticale.

Les forces pressantes sur les parois supérieure et inférieure

Les forces pressantes des parois supérieure et inférieure ne se compensent pas. La valeur de la force pressante sur la face supérieure est plus petite que celle sur la face inférieure.

Ceci s’explique par le fait que la pression augmente lorsque la coordonnée verticale diminue (d’après la loi fondamentale de la statique des fluides).

La résultante des forces pressantes

La résultante des forces pressantes appliquées sur l’objet est donc un vecteur vertical et dirigé vers le haut.

La poussée d’Archimède

est égale à la résultante des forces pressantes

qu’exerce un fluide sur un objet immergé dans ce fluide.

Son existence est due à la différence de pression entre la partie haute et la partie basse de l’objet.

c. Expression de la poussée d'Archimède

Un objet immergé dans un fluide (de masse volumique ρ) subit de la part de ce fluide, une poussée notée

, verticale et dirigée vers le haut, dont la valeur est égale au poids du fluide déplacé par l’objet.

avec :

F_PA la poussée d’Archimède subie par l’objet, en newton (N)
m_fluide la masse du fluide déplacé par l’objet, en kg
V_fluide le volume du fluide déplacé, en m³
ρ la masse volumique du fluide, en kg·m^–³
g l’intensité de la pesanteur, en N·kg^–¹

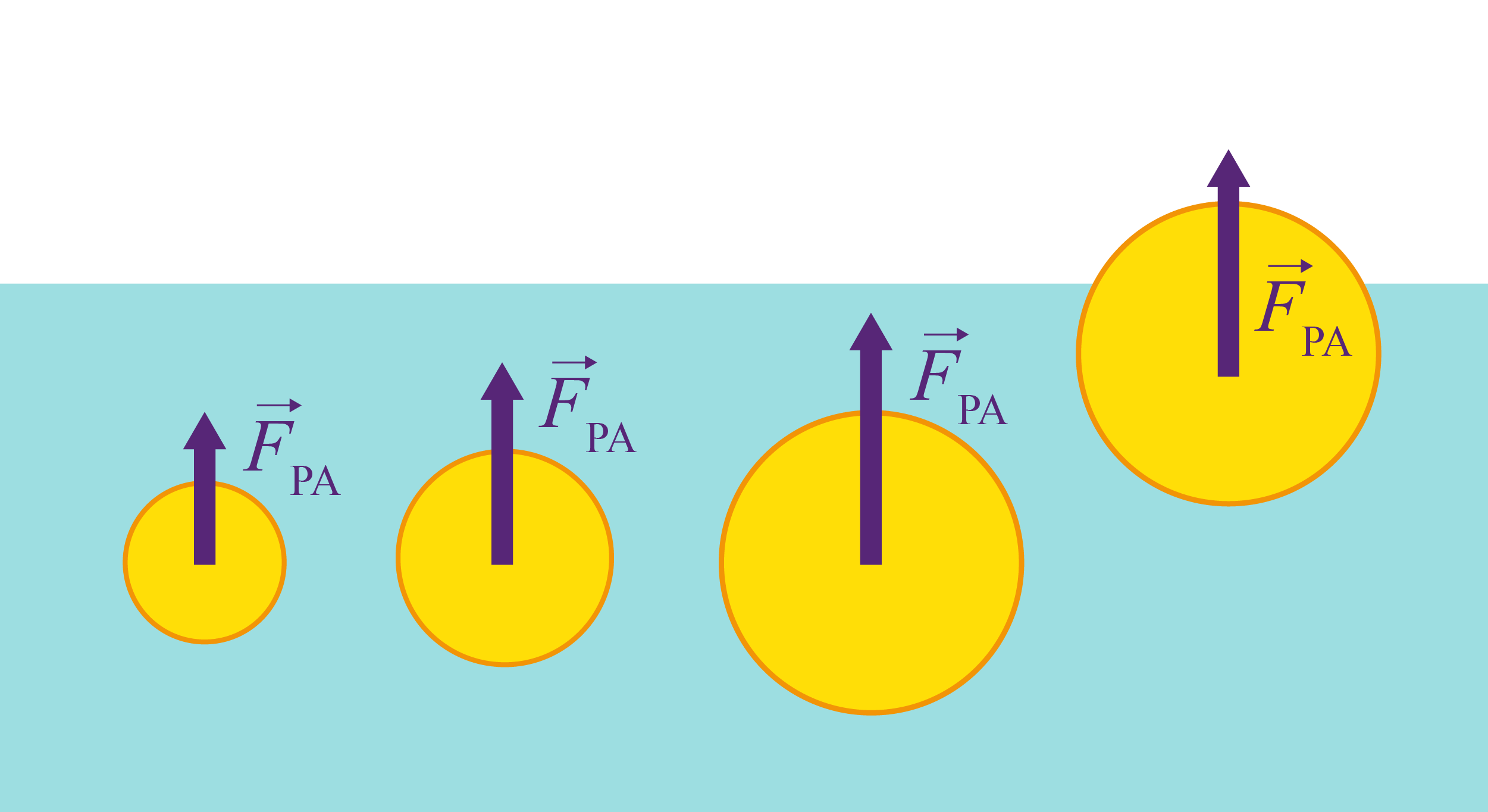
Illustration de quelques poussées d’Archimède

Pour un corps partiellement immergé, il ne faut tenir compte que du volume immergé pour le calcul de la poussée d’Archimède.

Le point d’application de la poussée d’Archimède est le centre de masse de la partie immergée de l’objet.

2. Exploiter la poussée d'Archimède

Le principe de la poussée d’Archimède est exploité pour la flottaison des bateaux ou alors pour les mouvements ascendants-descendants des sous-marins.

Flottaison des bateaux

Malgré son poids, un bateau flotte car son grand volume est essentiellement rempli d’air : si le bateau était totalement immergé, la valeur de la poussée d’Archimède serait supérieure à celle du poids du bateau.

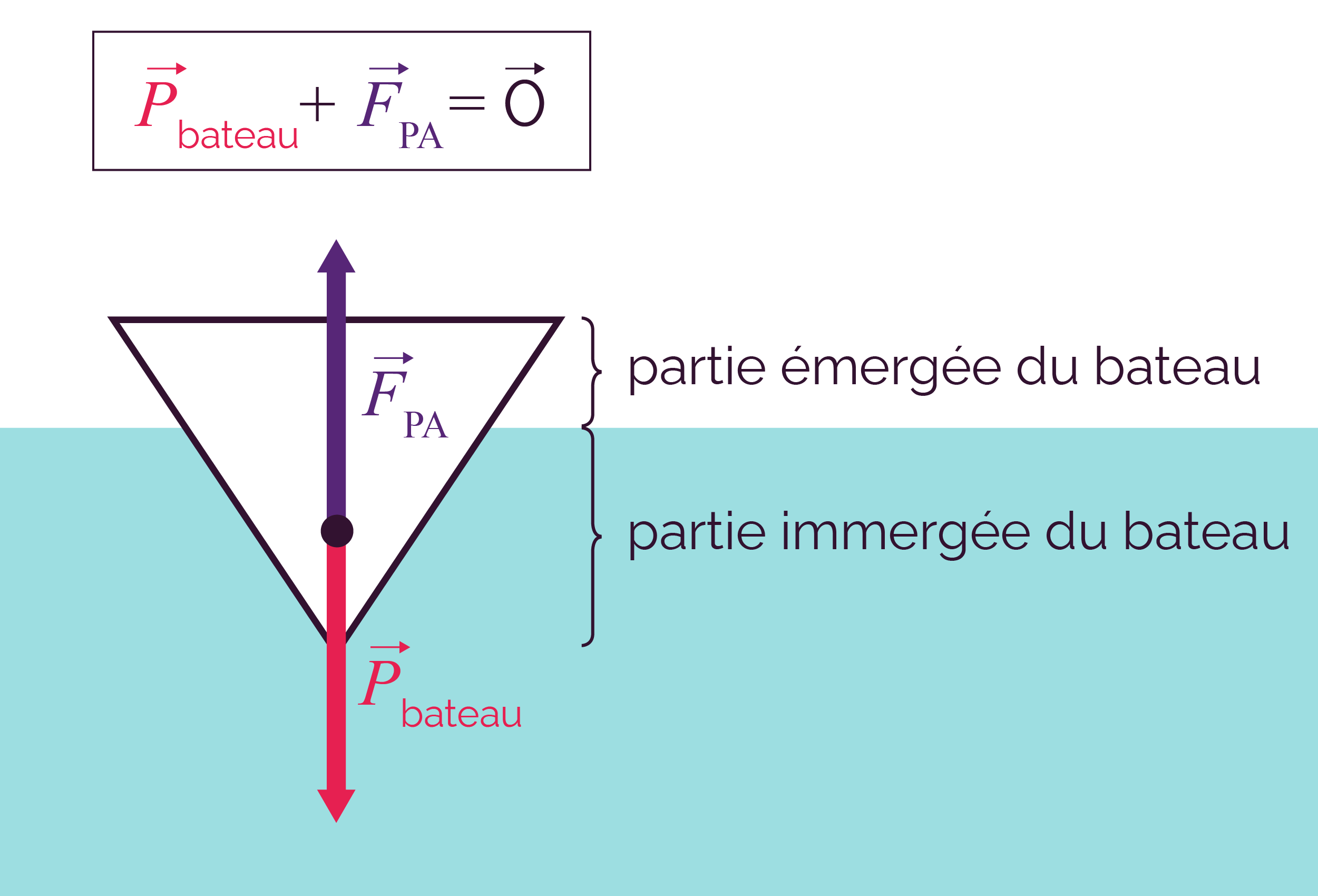
Flottaison d’un bateau

Mouvement vertical d’un sous-marin

Un sous-marin possède des ballasts qui sont des caissons pouvant être plus ou moins remplis par l’eau de mer.

Lorsque les ballasts se remplissent d’eau, le poids du sous-marin augmente : comme la poussée d’Archimède ne varie pas (le volume occupé par le bateau reste le même), le poids plus important du sous-marin lui permet d’amorcer un mouvement descendant.

Si on vide les ballasts, le poids du sous-marin diminue : comme la poussée d’Archimède ne varie pas, le poids moins important du sous-marin lui permet d’amorcer un mouvement ascendant.