Étudier un mouvement dans un accélérateur de particules
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Établir et exploiter les équations horaires du mouvement d'une particule accélérée entre les armatures d'un condensateur.
- Déterminer la vitesse d'une particule à la sortie du condensateur.
- Comprendre le principe d'un accélérateur de particules.
- Le champ électrique qui règne entre deux plaques parallèles, chargées de manière opposée (condensateur), est un champ uniforme : le vecteur associé est le même en tout point.
- L’étude du mouvement d’une particule chargée dans ce champ électrique se fait à l’aide de la deuxième loi de Newton. Le référentiel d’étude est le référentiel terrestre supposé galiléen. La particule de charge q est introduite par une ouverture dans la plaque dont la charge est de même signe, sans vitesse initiale.
- L’application de la deuxième loi de Newton permet d’obtenir les équations horaires du mouvement, qui montrent que le mouvement est rectiligne et accéléré. Le théorème de l’énergie cinétique permet de trouver la vitesse de la particule à sa sortie par une ouverture dans l’autre plaque.
- Un accélérateur de particules linéaire utilise ce principe pour réaliser des faisceaux de particules chargées à très haute vitesse. On les utilise en recherche dans le domaine de la physique des particules ou en médecine pour réaliser des radiothérapies.
- La deuxième loi de Newton
- L’énergie cinétique
- Dérivée, primitive
On étudie le mouvement d’une particule
chargée de charge q, de
masse m
négligeable, dans une zone où
règne un champ
électrique 
.
Ce champ électrique est créé entre les armatures d’un condensateur. Un condensateur est composé de deux plaques métalliques parallèles qui portent chacune une charge électrique opposée : +Q et –Q.
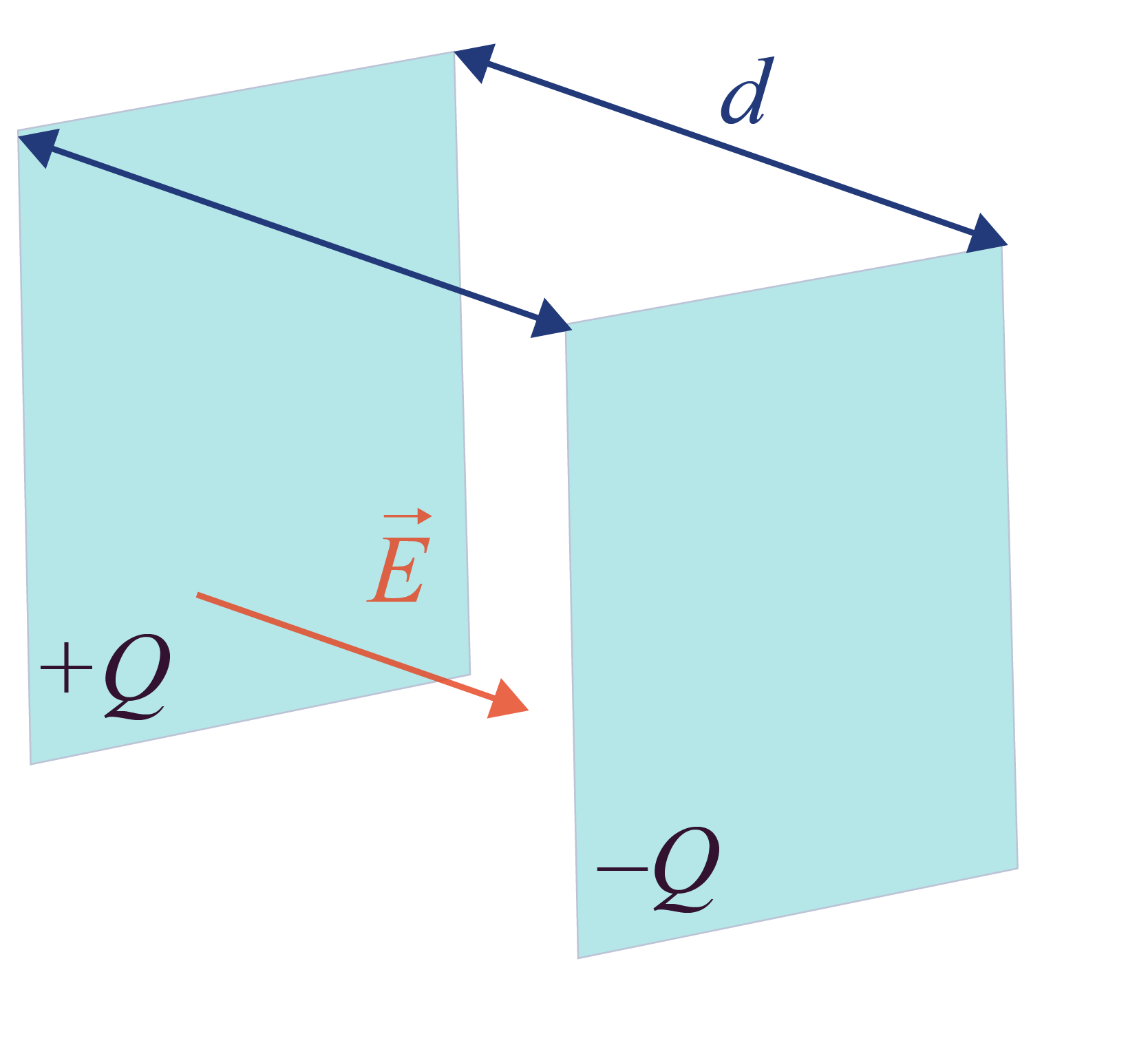
Schéma d’un condensateur
La valeur E de ce champ électrique est donnée par la relation suivante.
|
avec :
|
Une tension électrique est une grandeur algébrique, c’est-à-dire qu’elle peut être positive ou négative.
exercée
On réalise sur chacune des plaques une ouverture
d’entrée et de sortie et on place, sans
vitesse initiale, une particule chargée de
charge q positive au niveau de
l’ouverture réalisée dans la plaque
chargée positivement. On définit un
repère 
.
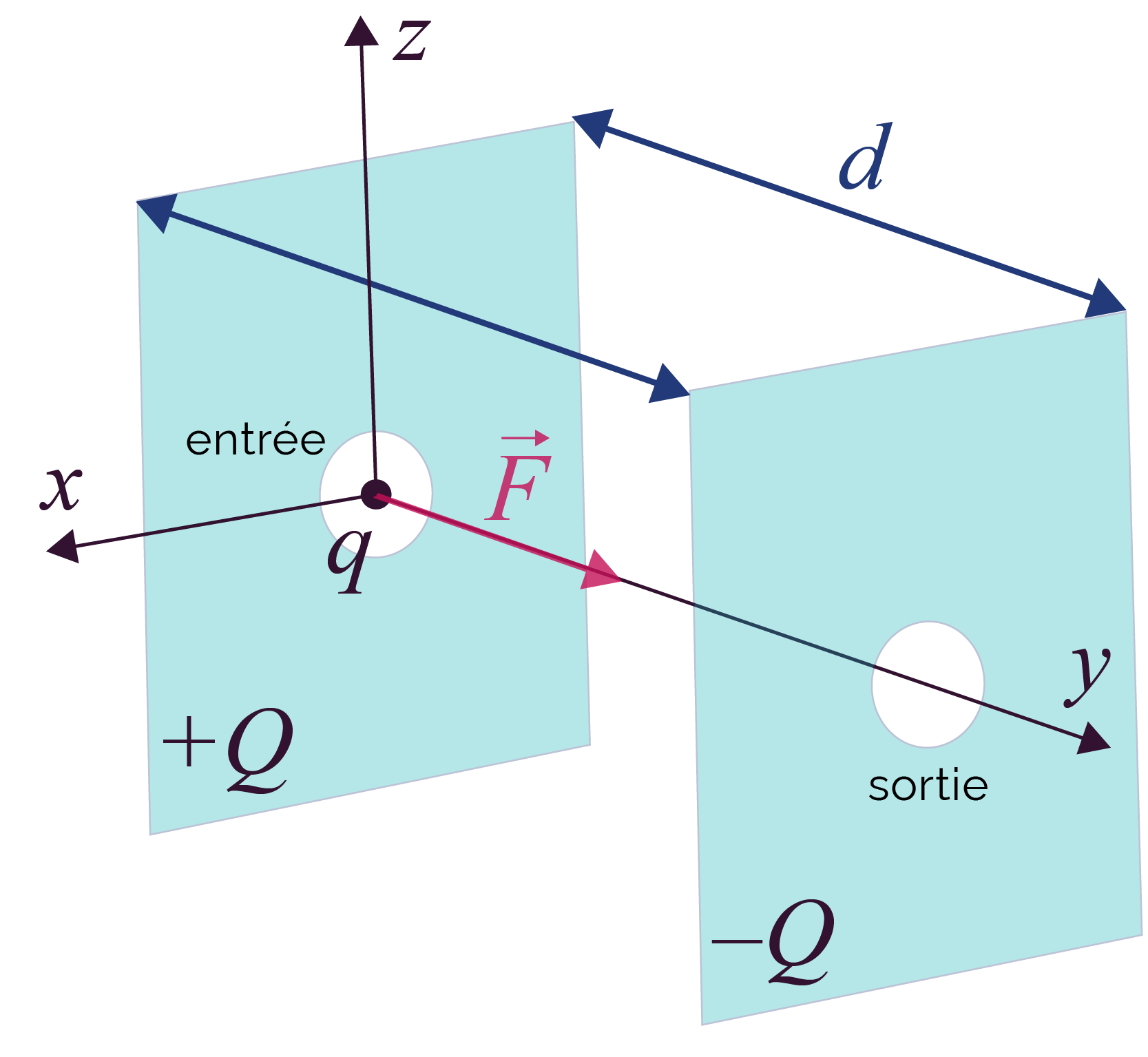
Repère et position initiale de la particule
La force électrique exercée par le champ électrique
va attirer cette particule vers la plaque
chargée négativement.
|
avec :
|
Afin de déterminer quel type de mouvement va avoir la particule, on détermine les équations horaires du mouvement, qui correspondent aux expressions des coordonnées en fonction du temps. On applique pour cela la deuxième loi de Newton à cette particule ponctuelle dans le référentiel terrestre supposé galiléen.
La résultante des forces se limite à la force électrique car on peut négliger le poids de la particule (sa masse est négligeable).
Condition initiale :
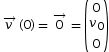et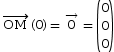 
Deuxième loi de Newton :
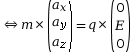
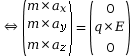
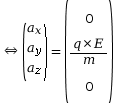
On cherche les primitives de chaque coordonnée pour obtenir les coordonnées du vecteur vitesse, et on cherche les constantes en appliquant les conditions initiales.
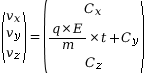
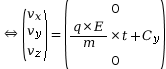
On cherche les primitives de chaque coordonnée pour obtenir les coordonnées du vecteur position, et on cherche les constantes en appliquant les conditions initiales.
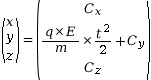
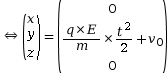
On constate que le mouvement est rectiligne et se fait selon l’axe (Oy). Ce mouvement est uniformément accéléré car la valeur de l’accélération est constante et positive.
Pour calculer la vitesse de la particule à la sortie du condensateur (par l’ouverture dans la plaque chargée négativement), on applique le théorème de l’énergie cinétique entre l’entrée et la sortie de la particule.
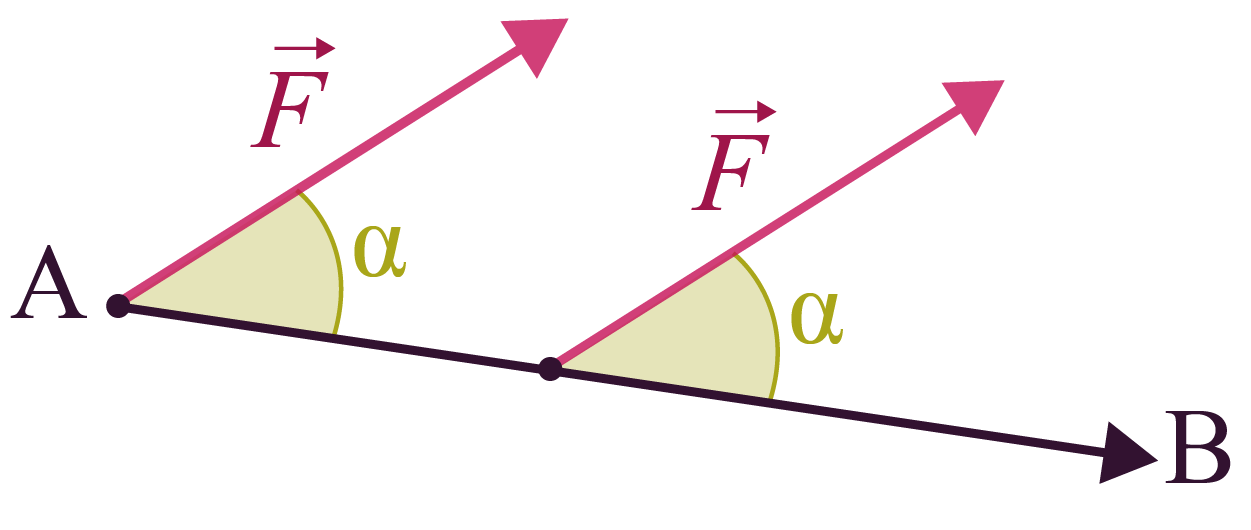
Force appliquée lors d’un déplacement
Le travail d’une force
constante 
sur un trajet AB est égal
à 
.
Pour la particule chargée, on a AB = d, F = q × E
et α = 0
soit cos(α) = 1.
On obtient 
.
La vitesse à l’entrée est nulle, le théorème de l’énergie cinétique s’écrit donc de la manière suivante.
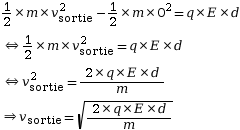
On peut de même réaliser l’accélération d’une particule chargée négativement en la plaçant dans l’ouverture de la plaque du condensateur chargée négativement.
Dans un accélérateur linéaire, les particules chargées sont accélérées à chaque fois qu’elles pénètrent dans un dispositif (qui fonctionne sur le même principe que le condensateur) où règne un champ électrique qui est convenablement dirigé et orienté : le champ électrique a la même direction que la vitesse de la particule et se trouve :
- dans le même sens qu’elle si la particule est positive ;
- dans le sens opposé si la particule est négative.
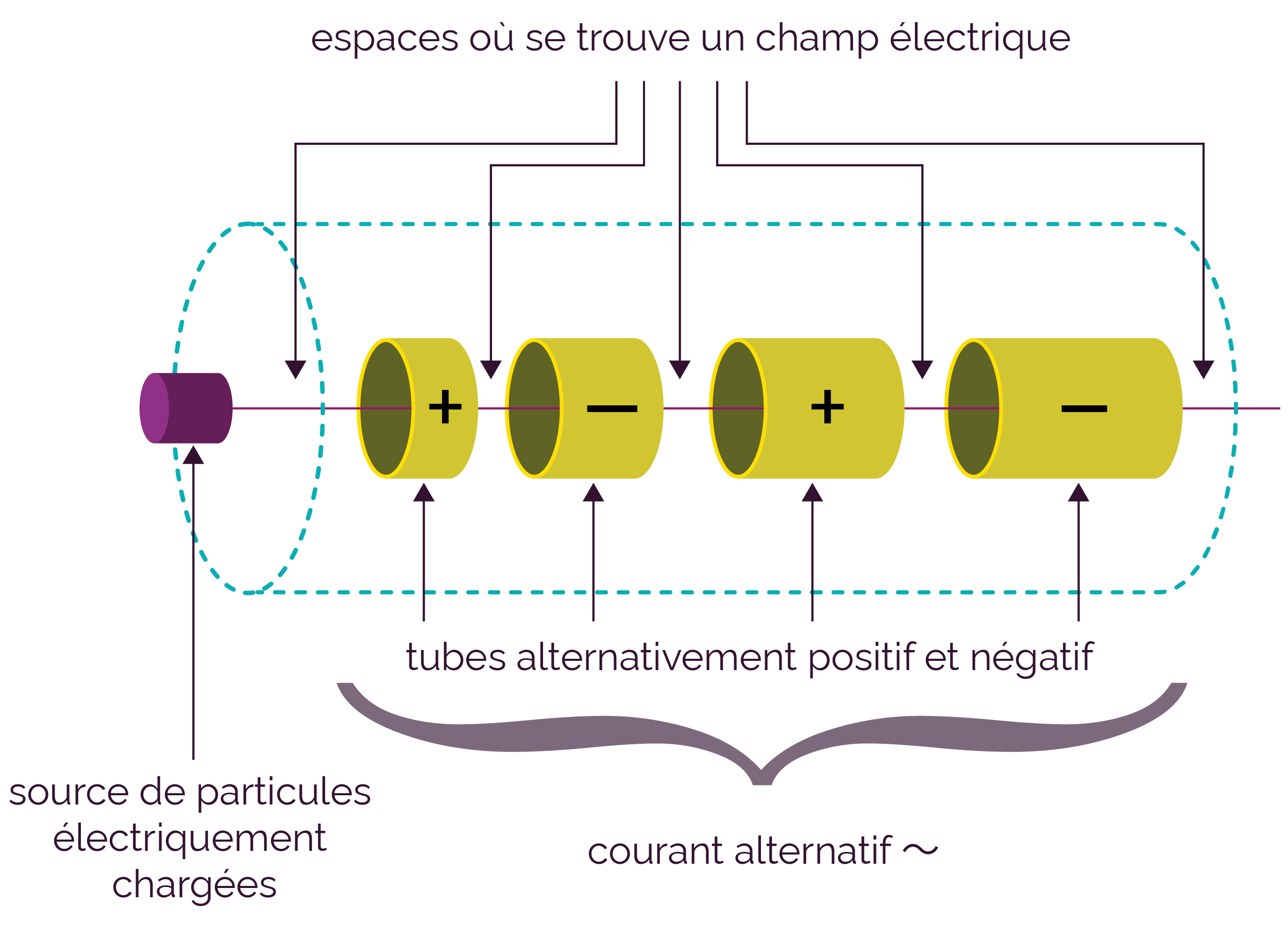
Principe d’un accélérateur linéaire
La fréquence de la tension alternative appliquée entre deux tubes consécutifs et la longueur des tubes sont telles qu’au passage des particules, le champ électrique permet une accélération de ces particules.
Un accélérateur linéaire de particules est utilisé dans les centres de recherche sur les particules, pour réaliser des collisions entre particules, ou alors comme accélérateur primaire dans les accélérateurs circulaires.
On les utilise également maintenant en médecine pour la radiothérapie : les particules accélérées permettent de détruire de manière localisée les cellules cancéreuses.
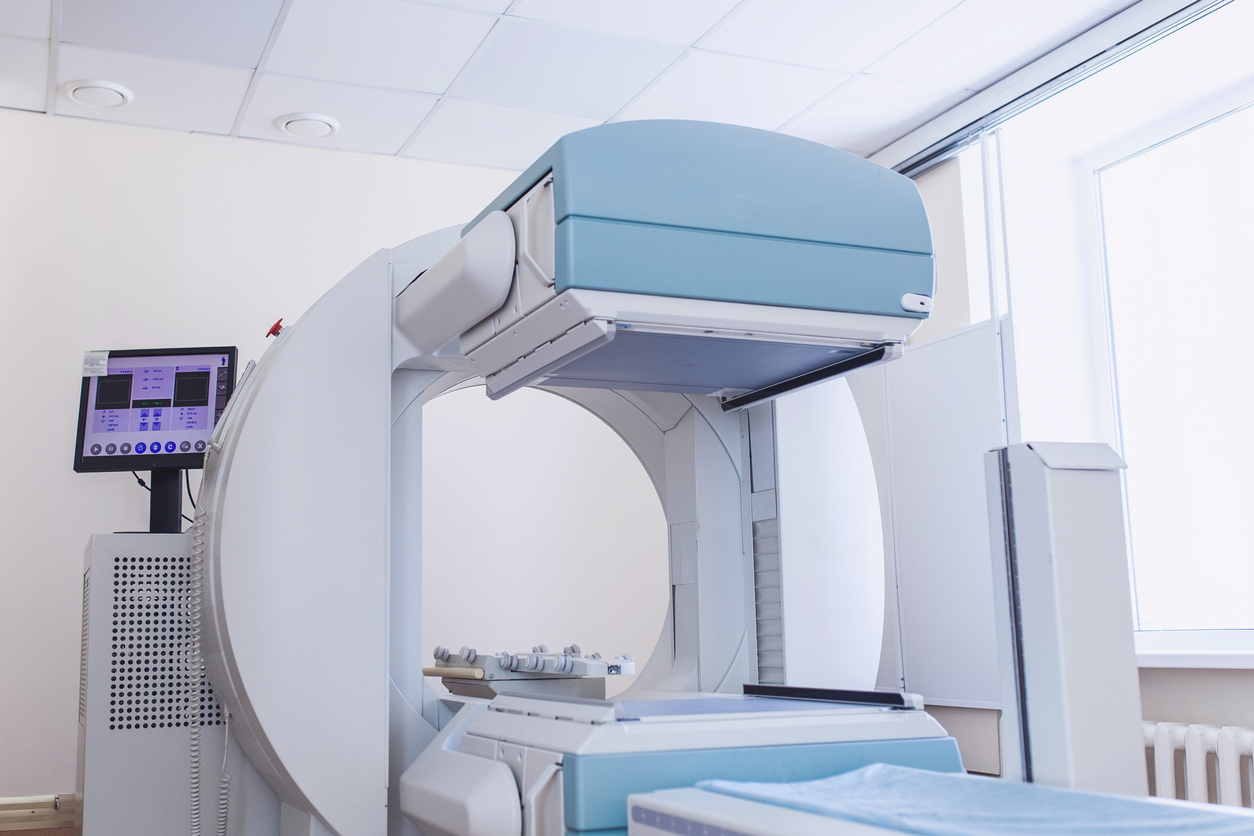
Accélérateur linéaire d’électrons
pour le traitement du cancer
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Physique Chimie
Exploiter une vidéo - Équations horaires et évolution des énergies
Physique Chimie
Exploiter la poussée d'Archimède
Physique Chimie
Tester la poussée d'Archimède
Physique Chimie
Exploiter la conservation du débit volumique
Physique Chimie
Exploiter la relation de Bernoulli
Physique Chimie
Exploiter l'équation d'un gaz parfait
Physique Chimie
Expliquer la variation d'énergie interne d'un système
Physique Chimie
Effectuer un bilan d'énergie sous forme de transfert thermique
Physique Chimie
Effectuer un bilan thermique du système Terre-atmosphère
Physique Chimie
Modéliser l'évolution de la température d'un système incompressible
Fermer
Accédez gratuitement à
