Dérivée et sens de variation d'une fonction

Remarques :
• pour le vocabulaire mathématique, "positive" signifie "positive ou nulle" (et "négative" veut dire "négative ou nulle"). Dans le cas d’une inégalité stricte, on précisera que la dérivée est "strictement positive/négative" et que f est "strictement croissante/décroissante".
• si la dérivée est nulle sur tout l’intervalle, la fonction est constante sur cet intervalle.

Exemple : la fonction est définie sur . Sa dérivée est toujours positive (ou nulle pour x = 0). Cette fonction est donc croissante sur son domaine de définition.

Cas particulier : si une fonction conserve le même sens de variation sur tout un intervalle (croissante ou décroissante), on dit que cette fonction est monotone.

Il est commode de regrouper toutes les indications obtenues sur la fonction dans un tableau appelé tableau de variations de la fonction.

Exemple 1 :
Soit définie sur .
Calculer sa dérivée, en chercher le signe, puis donner les variations de cette fonction sous forme de tableau.

• Calcul de la dérivée :

• Signe de la dérivée : la dérivée s’annule pour x = -2 ou x = 2.
On fait alors un tableau de signe qui indique que la dérivée est positive sur =]-∞ ; -2], négative sur =]-2 ; 2[ et positive sur =[2 ; +∞[.

• Variations de la fonction : on calcule les valeurs de la fonction pour les valeurs du tableau de signe(pour -2 et 2) :
f(-2) = 17 et f(2) = -15.

• Tableau des variations de f (dans lequel on fait figurer tous les éléments que l'on vient de déterminer) :

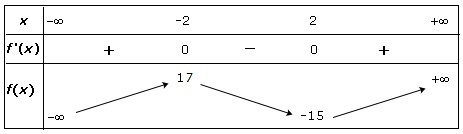
Remarque : les valeurs en -∞ et +∞ ne sont pas au programme des classes de premières (cours de terminale sur les limites).
Enfin, on peut utiliser une calculatrice (c’est conseillé !) pour tracer la courbe représentative de la fonction et vérifier que le tableau de variations est correct.

Exemple 2 :
Soit définie sur ]0 ; +∞[. Calculer sa dérivée, en chercher le signe puis dans un tableau donner les variations de cette fonction.
f est de la forme donc avec   .
.
Le dénominateur est un carré, donc toujours positif (il ne peut pas être nul sur le domaine de définition).
Le signe de la dérivée est alors celui du numérateur, soit strictement négatif.
Cette fonction est strictement décroissante sur son domaine de définition. On dit qu’elle elle est strictement monotone.

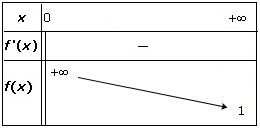
Remarque : la valeur 0 est interdite. On le signale en mettant une double barre verticale.

Par exemple, pour la fonction précédente définie sur ]0 ; +∞[, on a un minimum (absolu) qui vaut 1.
Pour l’autre fonction définie sur , on a un maximum (local) pour x = -2 qui est 17 et un minimum (local) pour x = 2 qui est -15.

Remarque : le pluriel de « extremum » est « extrema ».

D’après les variations de la fonction définie sur :

On peut déduire par exemple que l’équation f(x) = 0 aura 3 solutions dans :
• une solution sur l’intervalle ]-∞ ; -2] car la fonction prend des valeurs négatives puis positives, donc elle doit passer par 0
• une autre solution sur l’intervalle ]-2 ; 2] car la fonction prend des valeurs positives puis négatives, donc elle doit passer par 0
• une troisième solution sur l’intervalle ]2 ; +∞[ car la fonction prend des valeurs négatives puis positives, donc elle doit passer par 0.

Remarque : on peut déduire le nombre de solutions, pas leurs valeurs. Pour cela, on fera une recherche par approximation (par exemple avec un algorithme).